ISSN 0798 1015

Vol. 41 (Nº 09) Año 2020. Pág. 14

Las creencias de los futuros maestros sobre la enseñanza y aprendizaje de las matemáticas

Beliefs of preservice teachers on the mathematics teaching and learning

GARCÍA-MOYA, Melody 1; GÓMEZ-ESCOBAR, Ariadna 2; SOLANO-PINTO, Natalia 3 y FERNÁNDEZ-CÉZAR, Raquel 4

Recibido: 04/11/2019 • Aprobado: 04/03/2020 • Publicado: 19/03/2020

Contenido

1. Introducción

2. Metodología

3. Resultados

4. Discusión y conclusiones

Referencias bibliográficas

1. Introducción

Las Matemáticas generalmente resultan una asignatura difícil para los estudiantes. Esa visión negativa puede estar contribuyendo al descenso de estudiantes matriculados en carreras científicas y técnicas que tienen la asignatura de Matemáticas, conocidas como STEM (Ciencias, Tecnología, Ingeniería y Matemáticas) en el mundo anglosajón, que se viene observando desde hace varias décadas. Sin embargo, la sociedad actual demanda personas competentes en Matemáticas y capaces de aprender durante toda su vida, así como con capacidad de adaptación a los múltiples y rápidos cambios a los que nos obliga la revolución tecnológica en la que estamos inmersos. Por tanto, el desarrollo de la competencia matemática, estrechamente relacionada con la tecnología y su uso, es más que nunca una necesidad. Esta competencia se alcanza mediante el aprendizaje, que, aunque se produce de manera formal y no formal en todas las edades, el grueso del mismo sigue estando vinculado a la escuela. En ella encontramos dos elementos principales: los discentes y los docentes. Al respecto del primero se encuentran numerosas investigaciones que se han dedicado a determinar los aspectos cognitivos relacionados con las dificultades observadas en el aprendizaje de las Matemáticas. Por ejemplo, en el trabajo de Miranda y Gil (2000) se reportan como causas no solo las dificultades intrínsecas del contenido concreto, sino otras vinculadas con aspectos afectivos y emocionales que, según Gil, Blanco y Guerrero (2005), actúan sobre la metacognición del estudiante. Particularmente en niños de educación primaria este fenómeno afectivo ha sido ampliamente estudiado desde la psicología, y no tan extensamente desde la educación matemática. En el trabajo de Fernández-Cézar (2018), se revisan los trabajos sobre ansiedad hacia las Matemáticas en niños de educación primaria que, según la autora, son relevantes para ser tenidos en cuenta en el campo de la educación matemática, entre los cuales destaca que la ansiedad hacia las Matemáticas tiene un papel fundamental en la apertura o bloqueo de algunos caminos neuronales (Young, Wu & Menon, 2012) que facilitan o bloquean los aprendizajes. Además, se han desarrollado numerosas investigaciones al respecto de cómo se percibe el estudiante como aprendiz de matemáticas previo, incluso, al abordaje de ninguna tarea, indicando los hallazgos que cuando esa percepción es positiva o negativa refuerza sus sentimientos de éxito o frustración, respectivamente. Según Blanco y Guerrero (2002), la historia personal de cada estudiante contribuye al sentimiento que desarrolla al respecto de las Matemáticas, de manera que una secuencia de fallos repetidos lleva a este a cuestionarse su capacidad intelectual respecto de esta materia, incluso a considerar que cualquier esfuerzo para aprenderla será inútil. A esa sensación que tiene el estudiante, Gil, Blanco y Guerrero (2005) lo llaman el acto emocional, y lo identifican como una expresión de las creencias del estudiante sobre la naturaleza de la actividad matemática, sobre ellos como estudiantes o como parte de la clase. También Gómez-Chacón (1997) afirmaba que las creencias de los estudiantes son un aspecto fundamental para la configuración de la clase como realidad social, y lugar donde la enseñanza y el aprendizaje se desarrollan y toman sentido (Gómez-Chacón, 2000).

Por otro lado, están los docentes. La actitud de estos ante las Matemáticas ha sido estudiada en varios trabajos (Gómezescobar y Fernández-Cézar, 2018; Sayers, 2007; Sweeting, 2011; Thiel, 2010). Dado que la propia percepción de los docentes y cómo desarrollan su práctica pedagógica influye en las actitudes de su alumnado (Cézar, Suárez, Núñez y Leal, 2018), en sus manos estaría provocar un cambio en los afectos de los estudiantes hacia las Matemáticas. Si hay individuos en los que confluyan estas dos vertientes, la de docente y de discente, es en los estudiantes del Grado en Maestro, que son estudiantes y serán maestros en un futuro. Por ello sería de especial interés saber qué afectos tienen ellos frente a las Matemáticas, su percepción sobre su enseñanza y su aprendizaje, con el fin de contribuir a que ellos desarrollen, y contribuyan a desarrollar en su alumnado futuro, una visión de las mismas de utilidad e importancia, como sugieren sería necesario Gil, Guerrero y Blanco (2006), de manera que estos estudiantes en el futuro no temieran elegir carreras STEM porque tienen Matemáticas.

Es por eso que este trabajo pretende determinar las creencias de los estudiantes del Grado en Maestro (GM) al respecto de las Matemáticas, su enseñanza y aprendizaje.

1.1. Marco teórico

En las últimas cinco décadas se ha desarrollado una gran cantidad de investigaciones sobre la dimensión afectiva del individuo en el aprendizaje de las Matemáticas, entre los que destacamos por su repercusión internacional los trabajos de Gómez-Chacón (2000) en el ámbito iberoamericano, y los de McLeod (1988; 1992; 1994) en el anglosajón.

El dominio afectivo en educación matemática se considera compuesto por tres componentes (McLeod, 1992; Hannula et al., 2016): creencias, actitudes y emociones. Desde la filosofía de la ciencia, las creencias, su fijación y su definición se vienen estudiando desde el siglo XIX. Según Peirce en su ensayo titulado La fijación de la creencia (Sanders Peirce, 2007, p. 38) “Nuestras creencias guían nuestros deseos y dan forma a nuestras acciones” son aquello que dirige o gobierna nuestras acciones. Además, ya en el presente siglo, las creencias se consideran un componente del dominio afectivo de carácter cognitivo que puede influir en el comportamiento (Gómez-Chacón, 2003). Por lo tanto, las creencias sobre las Matemáticas y en cómo se percibe que tiene que ser su docencia podrían influir en la práctica docente del maestro de Matemáticas, o de los que lo serán en el futuro. Por ello, estudiar las creencias de los futuros maestros sobre las Matemáticas, sobre su enseñanza y aprendizaje, nos parece relevante, y constituye el objetivo principal de este trabajo.

Se encuentran varios estudios centrados en las creencias sobre las Matemáticas. Por ejemplo, Bermejo (1996) distinguió dos grandes categorías: las creencias sobre las Matemáticas, las cuales están influidas principalmente por el contexto escolar; y, las creencias de los estudiantes en relación con las Matemáticas, las cuales dependerían más del afecto, ya que estarían relacionadas con el autoconcepto y la confianza. Por otro lado, Gómez-Chacón (2000) destacó cuatro áreas de interés en el análisis de las creencias: identificar y describir las creencias sobre las Matemáticas como parte del sistema de creencias del individuo; determinar las influencias del sistema de creencias; conocer cómo se generan y se desarrollan los sistemas de creencias; y, buscar las condiciones para provocar un cambio de las mismas. En el ámbito anglosajón, McLeod (1992) diferenció cuatro ejes con respecto a las creencias: las creencias sobre las matemáticas, su enseñanza y aprendizaje; creencias acerca de uno mismo como estudiante de matemáticas; creencias acerca de la enseñanza de las matemáticas; y, creencias que surgen del contexto social. Este trabajo se centra en el primer eje reseñado por McLeod: las creencias sobre las matemáticas, su enseñanza y aprendizaje.

En la bibliografía analizada, se encuentran muchos trabajos al respecto de creencias sobre las Matemáticas de futuros maestros (Gil, Blanco y Guerrero, 2005; Gil, Nieto y Barona, 2006; Goldin, 1988a; 1988b; Gomez-Chacón, 1997; 2000; 2003; Hannula et al., 2016; McLeod, 1988; 1989; 1992; 1994). Pero no existen muchos trabajos que evalúen también las creencias de los futuros maestros sobre la enseñanza y aprendizaje de las Matemáticas.

Respecto a las creencias sobre las Matemáticas, los estudios revisados se basan en dos líneas de investigación, que son su relación con la práctica docente, y los cambios que pueden existir en las creencias iniciales (Cézar, Suárez, Núñez, y Leal, 2018). Sobre la relación entre creencias y la enseñanza-aprendizaje, no hay evidencias claras, pues las relaciones encontradas son inconsistentes, pero sí se indican en ellas factores que pueden influir. Por ejemplo, de acuerdo con Godino (2002), existen maestros de Matemáticas con conocimientos deficientes, lo que les impide solventar las dificultades que puedan tener sus estudiantes. Por otro lado, Contreras (2002) afirma que estas deficiencias de los maestros se evidencian cuando cometen errores similares a los de sus estudiantes, que no pueden, por lo tanto, corregir, al no ser ni siquiera conscientes de los mismos. Pero más allá del contenido matemático, no es menos importante el caso de los maestros que muestran aversión o miedo a las Matemáticas, lo cual les supone un estado de deficiencia emocional hacia la materia. Por otro lado, como afirmaba Padrón (2008), las deficiencias tanto cognitivas como afectivas de los maestros de Matemáticas desembocan en un empobrecimiento de la enseñanza, amenazando también la consolidación y el desarrollo de prácticas pedagógicas adecuadas. En resumen, el conocimiento matemático del profesor, sus prácticas pedagógicas y sus creencias hacia las Matemáticas podría comprometer su rendimiento y efectividad como docente de Matemáticas (Fernández, Prada y Solano, 2018).

Por otro lado, respecto a los instrumentos que se emplean para medir las creencias, se elaboran principalmente preguntas abiertas adhoc (Gil et al., 2005; Gil et al, 2006; Hannula et al., 2016), encontrándose muy pocos estudios que empleen cuestionarios con propiedades validadas psicométricamente, como el de Diego-Mantecón, Andrews, y Op’t Eynde (2007) que emplean con estudiantes de secundaria en distintos contextos socioculturales.

En las investigaciones al respecto de la enseñanza y aprendizaje de las Matemáticas encontramos algunos trabajos que analizan aspectos generales de la práctica de aula, como si emplean o no trabajo colaborativo, si realizan discusiones, etc. (Ross, Mcdougall, Hogaboam-Gray y Lesage, 2003), que no están expresamente relacionados solo con las Matemáticas. Otros trabajos se han realizado con el objeto de elaborar un modelo para la práctica docente en Educación Matemática (Godino, Contreras y Font, 2006; Font, Planas y Godino, 2010). Por otro lado, se encuentran trabajos focalizados en resaltar las buenas prácticas docentes, con el fin de apoyar la labor del profesorado de Matemáticas de distintas etapas educativas (Planas y Alsina, 2009).

Sin embargo, se encuentran pocos estudios que reporten evidencias sobre las prácticas de enseñanza de Matemáticas en Educación Infantil y Primaria. En esta línea está el trabajo de Vásquez (2010), que estudia la concepción de las maestras de preescolar sobre la enseñanza, el aprendizaje y la evaluación en Matemáticas, y concluye que prevalece la exposición y el aprendizaje memorístico. Se deduce que estos docentes entienden que de esta manera, al lograr que el niño repita, consiguen aprendizaje. Sin embargo, esta enseñanza expositiva de la Matemática no es considerada efectiva por el autor, pues el aprendizaje que consigue es meramente memorístico. Pero el estudio sí consigue desvelar que los maestros adecuan la instrucción a conseguir lo que ellos entienden por aprendizaje, que es la mera memorización.

Otro elemento fundamental que los docentes tienen en cuenta en el diseño de las prácticas de aula son los documentos o currículos oficiales. Estos se han ido desarrollando durante el pasado siglo en distintos países, entre ellos España. Consultando en concreto los currículos de Matemáticas más recientes (Real Decreto 126/2014 [rd 126/2014] (2014) para Educación Primaria, y Real Decreto 1105/2014 [rd 1105/2014] (2014) para ESO y Bachillerato), se observa que están orientados fundamentalmente a la adquisición de conocimientos. A pesar del cambio producido en las leyes europeas hacia las competencias entendidas como el “saber hacer”, lo que recoge la última ley española, la LOMCE (RD 126/2014 (2014) y RD 1105/2014 (2014)) son los estándares evaluables, formulados como indicadores de adquisición de contenidos. No existe en estos decretos ninguna referencia al dominio afectivo en relación con las Matemáticas, que sin embargo, sí se recoge en el currículo oficial para la Educación Infantil en Castilla la Mancha (D 67/2007) en forma de “competencia emocional”.

En los reales decretos para la educación obligatoria reseñados en el párrafo anterior hay escasas referencias a la práctica docente recomendada en el ámbito de las Matemáticas, hablando explícitamente solo de la resolución de problemas. Por otro lado, en otros ámbitos geográficos como EEUU, el National Council of Teachers of Mathematics (NCTM, 2003) sí recoge orientaciones claras para la adecuada enseñanza de las Matemáticas, focalizada en los procesos y no solo en los contenidos. En línea con la presencia de los procesos matemáticos en la práctica docente encontramos el trabajo de Coronata (2014) sobre docentes chilenos. Pero en la enseñanza-aprendizaje de las Matemáticas, también es importante la gestión del aula. Por ello, aparte de contenidos y procesos, también es fundamental considerar el papel del profesor, la propia enseñanza de las Matemáticas, el aprendizaje y la instrucción, como se recoge en el trabajo de Godino et al (2003). Estos aspectos son importantes debido a que es el profesor quien organiza las diferentes situaciones didácticas que pueden darse en el aula, siendo también él quien guía y aumenta los aprendizajes de los estudiantes por medio de la instrucción. Sin embargo, no se encuentran trabajos que estudien las creencias sobre las Matemáticas y su enseñanza y aprendizaje, así como la posible relación entre ellos, en los que serán futuros maestros.

Por todo lo anteriormente expuesto, en este trabajo se pretende analizar las creencias que los futuros maestros tienen al respecto de las Matemáticas, su enseñanza y aprendizaje, y estudiar, si existieran, relaciones entre las mismas.

El presente trabajo es de naturaleza exploratoria, y se emplea una metodología cuantitativa y correlacional.

2.1. Participantes

La muestra es de conveniencia y está formada por 143 estudiantes (123 mujeres). Los participantes se encontraban en el 1º curso de Grado en Maestro de Educación Primaria (GMEP) y 2º curso de Grado en Maestro de Educación Infantil (GMEI) en el año académico 2016/2017. Los estudiantes del GMEP cursaban la asignatura anual de “Didáctica de los números y la estocástica” y los del GMEI la asignatura cuatrimestral de “Desarrollo del pensamiento lógico y numérico en la educación infantil”.  Todos ellos formaban parte del alumnado de Grado de Maestro de la Universidad de Castilla-La Mancha.

2.2. Instrumentos

Para caracterizar las creencias de los futuros maestros sobre las Matemáticas y sobre su enseñanza-aprendizaje, se emplearon dos cuestionarios conocidos: el cuestionario de creencias sobre la enseñanza y aprendizaje de las Matemáticas de Godino, Batanero y Font (2003, p.53-54), y el cuestionario de creencias de Baroody y Coslick (1998), que ya ha sido utilizado en otros trabajos con maestros en servicio (Fernández et al, 2017; Fernández, Prada y Solano, 2018).

El primero consta de dos bloques. En el bloque primero (Tabla 1) se plantean los ítems mediante diferencial semántico, indicando el 1 y 2 el acuerdo con el enunciado de la izquierda, el 3 una posición neutra, y el 4 y 5 el acuerdo con el enunciado de la derecha. Su consistencia interna se midió con alfa de Cronbach, obteniendo.622.

Tabla 1
Cuestionario de Godino, Batanero y
Font (2003, p.53-54), bloque primero

En este cuestionario se encuentran los ítems 1, 4 y 7 que hacen alusión a la educación matemática, mientras que los ítems 2, 3, 5 y 6 tratan la creencia sobre el conocimiento, aprendizaje, instrucción efectiva y sobre qué es enseñar.

En el bloque segundo (Tabla 2) se señala el grado de acuerdo o desacuerdo por medio de una escala tipo Likert de 5 puntos, donde 1 es Totalmente en desacuerdo; 2, En desacuerdo; 3, Neutral; 4, De acuerdo; y 5, Totalmente de acuerdo. La consistencia interna se midió mediante alfa de Cronbach, obteniendo .609.

Tabla 2
Cuestionario de Godino, Batanero y
Font (2003, p.53-54), bloque segundo

En este bloque los ítems 1C, 4C y 9C tratan sobre la enseñanza-aprendizaje de las Matemáticas, los ítems 2C, 3C y 5C se centran en la instrucción y los ítems 6C, 7C y 8C son sobre el papel del profesor.

El cuestionario sobre creencias hacia las Matemáticas que se emplea está extraído del de Baroody y Coslick (1998, p 9. 1-8) y se muestra en la tabla 3 (alfa de Cronbach=.626). Está formado por 9 enunciados que se agrupan en ítems que reflejan diferentes creencias sobre las Matemáticas, al modo seguido en otros trabajos previos (Fernández, Prada y Solano, 2018). Se asumen tres categorías de creencias a partir de los grupos de teorías epistemológicas o patrones de organización matemática de Lakatos, publicadas en Gascón (2001): concepción Euclidiana que asume que las matemáticas se componen de hechos incuestionables; concepción Cuasi-empirista que considera a las Matemáticas como herramienta para entender el mundo; y concepción Constructivista, que considera que el saber matemático se construye sobre los conocimientos previos.

Tabla 3
Cuestionario de Baroody
y Coslick (1998 p. 1-8)

Al igual que en el cuestionario del bloque segundo, se indica el grado de acuerdo o desacuerdo por medio de una escala tipo Likert de 5 puntos, donde 1 es Totalmente en desacuerdo; 2, En desacuerdo; 3, Neutral; 4, De acuerdo; y 5, Totalmente de acuerdo.

Sobre los valores de la consistencia interna de los tres cuestionarios se consideran razonables al ser en este caso en todos los bloques 9 o 10 los ítems y verse esta medida de la consistencia interna afectada por el número de los mismos, que es bajo. Sin embargo, estos valores son similares a los reportados en otros estudios ya publicados, como el de Kumar y Morris (2005) o el de Hair, Black, Babin y Anderson (2010, p. 816).

2.3. Procedimiento

Los participantes fueron informados sobre la finalidad del estudio y su participación en el mismo fue voluntaria. Para participar en el estudio firmaron el consentimiento informado.

Los dos instrumentos se pasaron a los estudiantes al inicio de la asignatura indicada en la descripción de la muestra.

2.4. Análisis estadístico

Para el tratamiento informático de los datos se utilizó el paquete estadístico SPSS V. 24.

En el bloque primero del primer cuestionario (Tabla 1) se tomaron los valores 1 y 2 para determinar el acuerdo con la afirmación de la izquierda; los valores 4 y 5 para determinar el acuerdo con la afirmación de la derecha y el valor 3 para determinar el valor neutro. En el bloque segundo (Tabla 2) se tomaron los valores 1 y 2 como desacuerdo, 4 y 5 como el acuerdo con la afirmación propuesta en cada ítem y el valor 3 como neutro.

La interpretación de las correlaciones se analizó según la formulación semántica de los ítems, y se evaluó mediante la R de Spearman, con nivel de significación .05.

Para el análisis del cuestionario de creencias sobre las Matemáticas (Tabla 3) se realizó un tratamiento similar al empleado en estudios previos en los que se utilizó este cuestionario (Fernández et al., 2017; Fernández et al., 2018): se agruparon los ítems del 1 al 3 para la categoría Euclidiana, del 4 al 6 para la Cuasi-empirista, y del 7 al 9 para la Constructivista. Se consideró que un estudiante mostraba tener unas creencias sobre las Matemáticas de un único tipo si su puntuación superaba 9 en una sola de las categorías. Si lo superaba en más de una categoría, se consideró que sus creencias son mixtas.

3. Resultados

En la tabla 4 se muestran los valores de acuerdo con el bloque primero del cuestionario 1.

Tabla 4
Porcentajes de acuerdo con ítems indicados a la izquierda (B)
y a la derecha (A), del cuestionario 1, bloque primero

Los resultados del acuerdo y desacuerdo con el bloque segundo del cuestionario 1 se muestran en la tabla 5.

Tabla 5
Porcentajes de acuerdo y desacuerdo con los
ítems del cuestionario 1, bloque segundo

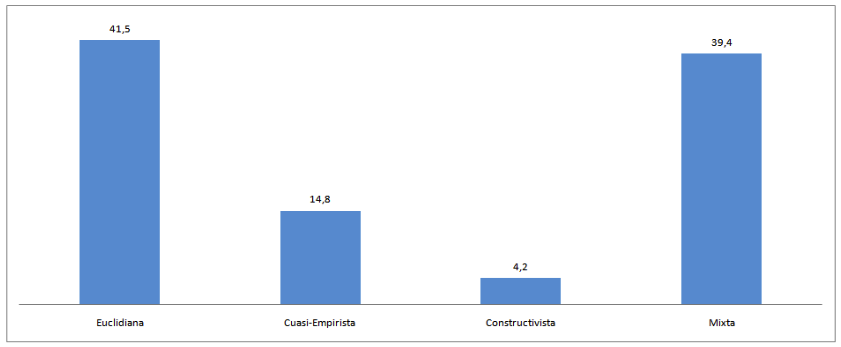
Por otro lado, los resultados sobre las creencias sobre las Matemáticas (ver cuestionario en Tabla 3) se muestran en la Figura 1. Se calculó el porcentaje de estudiantes que presentan las diferentes creencias hacia las Matemáticas, destacando que 41.5% tiene una creencia Euclidiana, seguido de 39.4% que tiene una creencia mixta. Por otro lado, se resalta que solo 4.2% de los participantes presenta una creencia constructivista.

Figura 1
Creencias hacia las Matemáticas (% para cada categoría)

En este trabajo se pretendía analizar las creencias que los futuros maestros tienen al respecto de las Matemáticas, su enseñanza y aprendizaje, así como la posible relación entre ellas. 

En la exploración, se analizaron los porcentajes de acuerdo con los ítems del bloque primero del cuestionario sobre enseñanza-aprendizaje de las Matemáticas.  Se observa un alto porcentaje de acuerdo en: 1A. El fin principal de la educación matemática es promover la comprensión y el pensamiento (75.2%); 2A. El crecimiento del conocimiento implica ganar nuevas comprensiones y reorganizar el propio pensamiento (74.3%); 3A. El aprendizaje es esencialmente un proceso activo de construir comprensiones y estrategias (80.9%); 5A. La implicación activa de los alumnos en el aprendizaje por descubrimiento y la solución de problemas es el modo más efectivo de estimular la comprensión y el pensamiento (64.5%); 6A. Enseñar es guiar- un profesor sirve principalmente para facilitar el descubrimiento y el pensamiento (75.7%). Todas estas afirmaciones están situadas a la derecha del diferencial semántico, e interpretamos que se corresponden con una visión activa del aprendizaje y la enseñanza, así como con una visión constructivista del mismo y centrada en el aprendiz. Se deduce que nuestros resultados no se alinean con los de Caballero et al. (2007), que reportaron que los futuros maestros percibían el aprendizaje matemático como mayoritariamente memorístico o mecánico, hallazgo también encontrado por Gil (2003) con alumnado de secundaria.

Por otro lado, se resalta que el 48.7% de los participantes están de acuerdo con la afirmación 4A, La construcción activa del conocimiento requiere hacer Matemáticas (esto es, descubrir patrones, hacer y comprobar conjeturas y resolver problemas), aunque hay también un 15.1% que está de acuerdo con la afirmación 4B, La memorización precisa de hechos y procedimientos y requiere que los niños estén atareados: que escuchen con atención y practiquen con diligencia lo que se les ha enseñado. El porcentaje de aquellos que están de acuerdo con un aprendizaje meramente memorístico es menor que el de aquellos que coinciden con la consideración de la construcción de saberes matemáticos de forma activa. Esto es consistente con la afirmación reportada en el párrafo anterior sobre que el aprendizaje debe ser construido con el aprendiz, y está en contra de la consideración memorística reseñada en trabajos previos (Caballero et al., 2007; Gil, 2003). Por otro lado, los participantes reparten su acuerdo de forma aún más equilibrada entre los extremos del ítem 7B, que expresa que los niños no tienen un interés natural en aprender Matemáticas, y que es esencial para los maestros estimular dicho aprendizaje (38.2%), y el ítem 7A, donde se dice que los niños tienen un interés natural en explorar y comprender cosas, siendo las Matemáticas interesantes en sí mismas (34.2%). Por lo tanto, este resultado divergente no permite concluir una mayoritaria percepción sobre el interés de los alumnos en las Matemáticas.

En el análisis del bloque segundo del cuestionario, los resultados indican un bajo porcentaje de acuerdo, el 4.6%, con 1C descartar los procedimientos no estándares porque pueden interferir con el aprendizaje del procedimiento correcto, y también un 16.4% con 4C que los niños pequeños son matemáticamente incapaces. Que el porcentaje de participantes de acuerdo con estos ítems sea bajo podría esperarse, y se considera positivo pues los futuros maestros estarían mostrando que no vinculan la corrección de los procedimientos con que estos sean los estandarizados, lo que abre su mente a la aceptación de propuestas de soluciones diversas. De otra parte, parece que no relacionarían la corta edad de los niños con la limitación de sus capacidades Matemáticas, lo cual corroboran muchos estudios sobre aprendizaje matemático en la infancia temprana (Alsina, 2015; Alsina y Roura, 2017; de Castro Hernández, López y García, 2015).  Los ítems en los que se recoge el papel del profesor son los 6, 7 y 8. Los participantes muestran porcentajes de acuerdo similares entre considerar al profesor un juez (6C, 26.3%), y que este actúe rápidamente deshaciendo desacuerdos (8C, 28.3%). Sin embargo, el porcentaje de acuerdo es mayor con la necesidad de que el profesor ofrezca feedback (7C, 44.1%). Las afirmaciones 2C y 3C se refieren a la instrucción matemática. Casi dos tercios de los participantes muestran acuerdo con que debería ir de los más simple a lo más complejo, siguiendo una secuencia sistematizada. En cuanto a que el trabajo individual fomente la independencia, ítem 9C, solo el 37.5% están de acuerdo con esta afirmación. Esto concuerda con lo que reportan Caballero et al. (2007) sobre que los futuros maestros rechazan mayoritariamente el trabajo individual para aprender Matemáticas, prefiriendo el trabajo en grupo.

Para analizar posibles relaciones al respecto de la consideración de la instrucción, qué es enseñar, el papel del profesor y el del alumno, así como de lo que se entiende por aprendizaje, se estudió la correlación entre las respuestas a los ítems del bloque primero. Se encontró que la respuesta al ítem 6 A guarda relación positiva y significativa con el 1 A (R=.229, p= .008), y con el 2 A (R=.201, p=.020), lo cual es esperable por considerar que el fin principal de la enseñanza matemática es promover la comprensión y el pensamiento, guiando en el camino hacia ganar nuevas comprensiones y reorganizando el propio pensamiento.

La afirmación 3 A tiene relación significativa con el ítem 5 A (R=.222, p=.010) y 6 A (R=.316, p<.000), lo cual es coherente si se considera que el aprendizaje es un proceso activo de construir comprensiones y estrategias, y que esto implica la participación activa del estudiante para el aprendizaje por descubrimiento, estimulando la comprensión y el pensamiento por medio de la actuación del profesor como un guía de los conocimientos a adquirir.

Por otro lado, los ítems del bloque segundo presentan las siguientes correlaciones positivas y significativas entre el tipo de instrucción y el papel del profesor: 6C y 7C (R=.258, p=.003), 7C y 2C (R=.225 p=.012), 8C y 6C (R=.400, p<.000). La visión que se manifiesta tiene que ver con que el profesor tiene que realizar la instrucción de manera que introduzca un tema matemático partiendo de lo simple hasta llegar a lo complejo, actuando con rapidez para eliminar desacuerdos entre los nuevos conocimientos a adquirir y las vivencias, y proporcionando un feedback inmediato y cercano al estudiante. Siguiendo con el papel del profesor y su relación con la instrucción, se encuentran también correlaciones positivas y significativas entre los ítems 3C y 5C (R=.279, p=.002), 7C y 3C (R=.249, p=.005), 8C y 3C (R=.232, p=.009), que versan sobre la metodología que el profesor debe utilizar en el aula. Así, tienden a considerar que la enseñanza debe iniciarse con las destrezas básicas y corregir con gran inmediatez las respuestas incorrectas, evitando así dar lugar a confusión.

Por otro lado, el ítem 6C tiene relación débil pero significativa con el 1C (R=.229, p=.008), 4C (R=.187, p=.035) y se relaciona con la consideración de que los niños pequeños son matemáticamente más incapaces. Bajo este supuesto, consideran que el profesor debe servir como un juez de los conocimientos que son válidos y los que no lo son, empleando para ello procedimientos estándares de aprendizaje, sobre todo con los niños más pequeños.

Se estudiaron también las correlaciones entre los ítems del bloque primero y los del segundo. Se obtuvieron correlaciones negativas y significativas entre 4A y 1C (R= -.224, p= .012), 4 A con 5C (R= - .261, p= 0.03) y 6C (R= -.289, p=.001), 6C con 5A (R= -.220, p= .013) y 4A (R= -.289, p= 0.01). Estas correlaciones negativas son esperables según los porcentajes de acuerdo mayoritarios mostrados por los participantes, y se derivaría de ellas que los participantes consideran que la construcción activa del conocimiento matemático requiere de procedimientos estándares, que el profesor no necesita una secuencia sistemática demasiado organizada, y que el profesor no debe ejercer el papel de juez, sino de guía del pensamiento a adquirir; debe estimular la implicación activa de los alumnos en el aprendizaje por descubrimiento y la resolución efectiva de problemas.

Por lo tanto, a la vista de estos resultados se podría decir que existen ciertas incongruencias al respecto de las creencias que muestran los futuros maestros de EP y de EI al respecto de la enseñanza y el aprendizaje de las Matemáticas, dado que si bien los participantes se muestran de acuerdo con que no se admitan solo métodos estandarizados, cuando se trata de la enseñanza con niños más pequeños apoyan que se utilicen los métodos didácticos estandarizados preferentemente. Es particularmente curioso dado que pareciera que entendieran que los niños pequeños no pudieran desarrollar sus propios métodos y estrategias matemáticas, y necesitaran una guía más estrecha, precisamente cuando son los que aún no conocen los métodos estandarizados por tener menos años de escolarización, y cuando también necesitan desarrollar los suyos propios, como en cualquier otra etapa educativa.

En suma, dado los porcentajes de acuerdo en los ítems sobre enseñanza-aprendizaje de las matemáticas (1A, 3A, 5A, 6A, 1C, 4C y 9C) e instrucción (4A ,7A, 2C, 3C y 5C), los participantes tienen una concepción constructivista del aprendizaje matemático, pues se afirma que los participantes creen que la implicación activa de los estudiantes en el aprendizaje facilita la comprensión y el pensamiento matemático apoyado todo eso por una enseñanza guiada del profesor. En cuanto al papel de este, (ítems 6C, 7C y 8C) se encuentra que un porcentaje alto de participantes muestra acuerdo respecto a que el profesor debe partir de lo simple e ir aumentando la complejidad realizando intervenciones inmediatas para alabar las respuestas correctas y corregir las incorrectas. Consecuentemente, de estas afirmaciones se derivaría que un porcentaje mayoritario de participantes tiene creencias constructivistas al respecto de la enseñanza y aprendizaje de las Matemáticas.

En cuanto a las creencias sobre las Matemáticas, parecería esperable que los participantes fueran mayoritariamente de creencias constructivistas. Sin embargo, no es lo que se encuentra en este trabajo, pues como se ve en la figura 1, solo 4.2% de los participantes tienen una visión constructivista de las Matemáticas. Hay casi el mismo porcentaje de aquellos que tienen creencias mixtas que aquellos de creencias euclidianas, y son muchos menos los que tienen creencias cuasi-empiristas. Por tanto, estos futuros maestros no coinciden mayoritariamente con la afirmación de Sanders Peirce (2007) sobre que la mente puede transformar el conocimiento, pero solo lo genera a través de la observación de lo que nos rodea, que encajaría con una concepción Cuasi-empirista de las Matemáticas. En línea con este resultado están los estudios previos realizados con maestros en servicio, como el de Fernández et al. (2018), que encuentran que los maestros españoles son mayoritariamente de creencias Euclidianas, mientras que los colombianos son mayoritariamente de creencia Cuasi-empiristas. Los segundos verían en las Matemáticas más utilidad que los primeros.

Estos hallazgos contrastan con la visión que tienen los mismos estudiantes al respecto de la enseñanza-aprendizaje de las Matemáticas. Suponemos que esta disociación que exhiben les debe hacer complicado imaginar cómo combinar una materia que consideran mayoritariamente compuesta por hechos fijos e inmutables, con un conocimiento sobre la misma que debe construir el alumno con la guía del maestro. Por lo tanto, concluimos que a pesar de que los futuros maestros tienen una percepción de la implicación activa del alumno en el aprendizaje, y del papel del maestro como guía del mismo, que podría considerarse una concepción constructivista de la enseñanza-aprendizaje de las Matemáticas, su concepción de las mismas Matemáticas no es mayoritariamente constructivista.

Reseñamos las limitaciones de este estudio, que no permiten generalizar las conclusiones, ya que se ha empleado una muestra de conveniencia. Por tanto, se hace necesario continuar con investigaciones de este tipo para ahondar en el conocimiento de las creencias sobre las Matemáticas, su enseñanza y aprendizaje de los futuros maestros.

Alsina i Pastells, Á. (2015). Matemáticas intuitivas e informales de 0 a 3 años: Elementos para empezar bien (Vol. 78). Narcea Ediciones.

Alsina, Á., y Roura, D. (2017). Estableciendo niveles de adquisición de conocimientos matemáticos informales antes de los 3 años: diseño, construcción y validación de una rúbrica. Edma 0-6: Educación Matemática en la Infancia, 6(1), 32-52.

Baroody, A.J., & Coslick, R.T.  (1998). Fostering Children' Mathematical Power: An Investigative Approach to K-8 Mathematics Instruction. Mahwah, NJ: Lawrence Erlbaum Associates.    

Bermejo, V. (1996). Enseñar a comprender las matemáticas. En J. Beltrán y C. Genovard (Eds.), Psicología de la Instrucción I (256-279). Síntesis. Madrid. España.

Blanco Nieto, L. J., y Guerrero Barona, E. (2002). Profesores de matemáticas y psicopedagogos. Un encuentro necesario. En Aportaciones de la didáctica de la matemática a diferentes perfiles profesionales (121-140). Universitat d´ Alacant/Universidad de Alicante.

Caballero, A., Blanco, L.J., y Guerrero, E. (2007). Las actitudes y emociones ante las matemáticas de los estudiantes para maestros de la facultad de educación de la universidad de Extremadura. En M. Camacho, P. Flores, y P. Bolea (Eds.), Investigación en Educación Matemática XI, La Laguna: SEIEM. Simposio llevado a cabo en en congreso de La Laguna, Tenerife.

Cézar, R. F., Suárez, C. A. H., Núñez, R. P., y Leal, P. R.(2018). Dominio afectivo y prácticas pedagógicas de docentes de Matemáticas: Un estudio de revisión. Revista Espacios, 39(23), 25. Recuperado de: http://www.revistaespacios.com/a18v39n23/a18v39n23p25.pdf

Contreras González, L. C. (2002). Dificultades y obstáculos para el cambio en el aula: una perspectiva desde la educación matemática. Revista Investigación en la Escuela, (47), 75-82. Recuperado de: http://www2.uhu.es/luis.contreras/Novedades/ articulo02.htm   

Coronata, C. (2014). Presencia de los procesos matemáticos en la enseñanza del número de 4 a 8 años. Transición entre la educación infantil y elemental (Doctoral dissertation, Tesis Doctoral. Universitat de Girona. Recuperada de: http://www. tdx. cat/handle/10803/284330).

de Castro Hernández, C., López, G. F., y García, M. R. (2015). Matemáticas con dos años: buscando teorías para interpretar la actividad infantil y las prácticas docentes. Tendencias pedagógicas, (26), 89-108.

Diego-Mantecón, J., Andrews, P., & Op’t Eynde, P. (2007). Mejora y evaluación de un cuestionario de creencias de matemáticas en función de nacionalidad, edad y sexo. En M. Camacho, P. Flores, y P. Bolea (Eds.), Investigación en Educación Matemática XI, La Laguna: SEIEM. Simposio llevado a cabo en en congreso de La Laguna, Tenerife.

Decreto 67/2007, de 29 de mayo, por el que se establece y ordena el Currículo del Segundo Ciclo de la Educación Infantil en la Comunidad Autónoma de Castilla-La Mancha. (DOCM, 1 de junio)

Fernández-Cézar, R. (2018) Children anxiety towards mathematics: A selective bibliographical review for mathematical Education. Journal of Research in Science, Mathematics and Technology Education, 1(1), 47-61. doi: 10.31756/jrsmte.113.

Fernández-Cézar, R., Iglesias, Albarrán, LM., Solano-Pinto, N., Rizzo, K.A., León-Mantero, C., y Gómez, H. (2017). Creencias, ansiedad y presencia de los procesos en la enseñanza de las matemáticas: un estudio en maestros. En C. Toboso Nieto (Presidencia). Conferencia llevada a cabo en el VIII CIBEM: Congreso Iberoamericano de Educación Matemática, Madrid, España.

Fernández-Cézar, R., Prada-Núñez, F., y Solano-Pinto, N., (2018). Beliefs towards Mathematics in Elementary Education Teachers: a comparative study. Journal of Research in Science, Mathematics and Technology Education, 1(3), 329- 345. doi: 10.31756/jrsmte.135

Font, V., Planas, N., y Godino, J. D. (2010). Modelo para el análisis didáctico en educación matemática. Infancia y aprendizaje, 33(1), 89-105.

Gascón, J. (2001). Incidencia del modelo epistemológico de las matemáticas sobre las prácticas docentes. Revista Latinoamericana de Investigación en Matemática Educativa, RELIME, 4(2), 129-159.

Gil, N. (2003). Creencias, actitudes y emociones en el aprendizaje matemático. Memoria de investigación de Doctorado no publicada. (Puede obtenerse en N. Gil, Universidad de Extremadura., Departamento de Psicología y Sociología de la Educación (06071). Badajoz.

Gil, N., Blanco, L. J., y Guerrero, E. (2005). El dominio afectivo en el aprendizaje de las matemáticas. Una revisión de sus descriptores básicos. Revista iberoamericana de educación matemática, 2(1), 15-32.

Gil Ignacio, N., Guerrero Barona, E., y Blanco Nieto, L. (2006). El dominio afectivo en el aprendizaje de las Matemáticas. Electronic Journal of Research in Educational Psychology, 4 (1), 47-72.

Godino, J. D. (2002). La formación Matemática y didáctica de maestros como campo de acción e investigación para la didáctica de las Matemáticas: El proyecto Edumat-Maestros. Recuperado de:  http://www.ugr.es/~jgodino/edumat-maestros/descripción.pdf 

Godino, J.D., Batanero, C., y Font, V. (2003). Fundamentos de la enseñanza y el aprendizaje de las matemáticas para maestros. Publicación realizada en el marco del Proyecto de Investigación y Desarrollo del Ministerio de Ciencia y Tecnología, BSO2002-02452.

Godino, J. D., Contreras, Á., y Font, V. (2006). Análisis de procesos de instrucción basado en el enfoque ontológico-semiótico de la cognición matemática. Recherches en didactique des Mathématiques, 26(1), 39-88.

Goldin, G.A. (1988a). Affective representation and mathematical problem solving. In Proceedings of the Tenth Annual Meeting on the Psychology of Mathematics Education, North American Chapter of International Group (Vol. 2, pp. 1-7). IL. USA.

Goldin, G. A. (1988b). The development of a modal for competence in mathematical problem solving based on systems of cognitive representation. In Proceedings of the Twelfth International Conference for the Psychology of Mathematics Education (International Group for the Psy (Vol. 2, pp. 358-365). Oak Printing House.

Gómezescobar, A. y Fernández-Cézar, R. (2018). Los maestros y sus actitudes hacia las matemáticas: un estudio sobre Educación Infantil y Primaria en España. UNIÓN, Revista Iberoamericana de Educación Matemática, (52), 186-200.

Gómez-Chacón, I. M. (1997). La alfabetización emocional en educación matemática: actitudes, emociones y creencias. Uno: Revista de didáctica de las matemáticas, 13, 7-22.

Gómez-Chacón, I. M. (2000). Matemática Emocional. Los afectos en el aprendizaje matemático. Narcea Ed. Madrid. España.

Gómez-Chacón, I. M. (2003). La tarea intelectual en matemáticas afecto, meta-afecto y los sistemas de creencias. Boletín de la Asociación Matemática Venezolana, 10(2),  225-247.

Hannula, M. S., Di Martino, P., Pantziara, M., Zhang, Q., Morselli, F., Heyd-Metzuyanim, E., & Goldin, G. (2016). Attitudes, Beliefs, Motivation, and Identity in Mathematics Education. En G.A. Goldin., M.S. Hannula., E. Heyd-metzuyanim., A. Jansen., R. Kaasila., S. Lutovac., P. Di Martino., F. Morselli., J.A. Middleton.,  M. Pantziara., y Q. Zhang (Eds.), Attitudes, Beliefs, Motivation and Identity in Mathematics Education, (pp. 1-359). Cham, Urang Campa: Springer.

Hair , J., Black , W., Babin , B., & Anderson , R. (2010). Multivariate data analysis (7th ed.). Upper saddle River, New Jersey: Pearson Education International.

Kumar, D., & Morris, J. D. (2005). Predicting scientific understanding of prospective elementary teachers: Role of gender, education level, courses in science, and attitudes toward science and mathematics. Journal of Science Education and Technology, 14(4), 387-391.

McLeod, D.B. (1988). Affective issues in mathematical problem solving: Some theoretical considerations. Journal for Research in Mathematics Education, 19, 134-141. McLeod, D. B. (1989a). The role of affect in mathematical problem solving. In Affect and mathematical problem solving (pp. 20-36). Springer, New York, NY. USA.

McLeod, D. B. (1989). Beliefs, attitudes, and emotions: New views of affect in mathematics education. In Affect and mathematical problem solving (pp. 245-258). Springer, New York, NY. USA.

McLeod, D.B. (1992). Research on affect in mathematics education: A reconceptualization. En D.A. Grouws (Ed.), Handbook of Research on mathematics Teaching and Learning (pp. 575-598). New York: Macmillan. USA

McLeod, D.B. (1994). Research on affect and mathematics learning in the JRME: 1970 to the present. Journal for Research in Mathematics Education, 25(6), 637-647.

Miranda, A., y Gil, D. M. (2000). Dificultades del aprendizaje de las matemáticas: un enfoque evolutivo. Editorial Aljibe. Archidona, Málaga. Spain.

NCTM. (2003). Principios y Estandares para la Educación Matemática,  Granada, España:  Servicio de Publicaciones de la SAEM Thales.

Padrón, O. J. M. (2008). Actitudes hacia la matemática. Sapiens. Revista Universitaria de Investigación, 9(1), 237-256.  

Planas, N., y Alsina, A. (2009). Educación matemática y buenas prácticas. Infantil, primaria,secundaria y educación superior. Barcelona, España: Editorial Graó.

Real Decreto 126/2014, de 28 de febrero, por el que se establece el currículo básico de la Educación Primaria.

Real Decreto 1105/2014, de 26 de diciembre, por el que se establece el currículo básico de la Educación Secundaria Obligatoria y del Bachillerato.

Ross, J. A.,  Mcdougall, D., Hogaboam-Gray, A., & Lesage, A. (2003). A survey measuring elementary teachers' implementation of standards-based mathematics teaching. Journal for Research in Mathematics Education, 34(4), 344-363.

Sanders Peirce, C. (2007). La fijación de la creencia. Cómo aclarar nuestras ideas. (Traducción de Lorena Villamil García). Oviedo, España: KRK Ediciones.

Sayers, J. (2007) Primary teachers’ attitudes towards and beliefs about mathematics teaching: the collective culture of one English primary school. Fifth Conference of the European Society for Research in Mathematics Education (CERME 5) Proceedings, Larnaca, Cyprus, 22-26 February 2007.

Sweeting, Kylie (2011). Early years teachers’ attitudes towards mathematics. (Tesis doctoral).Queensland University of Technology, Queensland.

Thiel, O. (2010). Teachers’ attitudes towards mathematics in early childhood education. European Early Childhood Education Research Journal, 18(1), 105-115.

Vásquez, O. G. (2010). Concepciones de las maestras de preescolar sobre la enseñanza, el aprendizaje y la evaluación de las matemáticas. Hexágono Pedagógico, 1(1),3-16.

Young, C. B., Wu, S. S., & Menon, V. (2012). The neurodevelopmental basis of math anxiety. Psychological Science, 23(5), 492-501.

1. Departamento de Matemáticas, área Didáctica.

2. Departamento de Matemáticas, área Didáctica.

3. Departamento de Psicología, área de Psicología Evolutiva y de la Educación. Facultad de Educación de Toledo, Universidad de Castilla la Mancha, España.

4. Departamento de Matemáticas, área Didáctica. Autora de correspondencia: raquel.fcezar@uclm.es