ISSN 0798 1015

Vol. 40 (Number 34) Year 2019. Page 14

Hybrid Method for Multi-Criteria Risk Minimization

Método híbrido para la minimización de multi-criterios de riesgo

SUKHORUKOVA, Irina Vladimirovna 1; FOMIN, Gennadij Petrovich 2; EKAREVA, Irinda Leonidovna 3 & MUSHRUB, Vladimir Aleksandrovich 4

Received: 14/06/2019 • Approved: 20/09/2019 • Published 07/10/2019

Contents

1. Introduction

2. Literature survey

3. Methodology

4. Results

5. Conclusions

Bibliographic references

1. Introduction

The relevance of the presented research is stipulated by the need to find an optimal solution in business activities that meets many different criteria often contradicting each other. The solution to the problem is reached through enumerating possibilities to find solutions, each of which surpasses the other by at least one of the specified criteria (Sukhorukova I.V. & Chistyakova N.A., 2018). A large number of such solutions are called the best ones according to Pareto.

The task of searching for a set of optimal solutions is quite time-consuming, with classical methods of optimization deemed practically unsuitable. To solve this problem it is necessary to find not only a set of solutions that meet the specified criteria, but also to achieve the maximum distinction between these solutions, and accordingly, to find a larger number of these options (Belton V., 2002; Hesham K.A. & Salih O.D, 2008). Therefore, it is necessary to find a point in the area of acceptable solutions to the issue under consideration, which minimizes or maximizes the whole set of characteristics. Thus, for example, a seemingly simple task of generating a product range includes a lot of important issues: selection of model and brand of goods, logistics chain, time of purchase and delivery of goods, choosing a financial transaction scheme, solution tool, choosing an expert to advise on minimizing the risks of each operation, implementing the plan as a whole and avoiding fraud to successfully reach the objective. At the same time, there is a clear desire to achieve maximum efficiency at the lowest cost, choosing an investment solution when it is necessary to get the maximum benefit with the least risk. (Chistyakova N.A. & Sukhorukova I.V, 2018). However, the decision which simultaneously would satisfy the set of inconsistent requirements, as a rule, does not exist, and hence the decision is accepted in the conditions of risk. In this case, it is necessary to consult with specialists to ensure the implementation of the solution and particularly, to use non-formalized methods of searching for a solution. Finding an optimal solution provides a balanced solution to financial and economic problems, significantly saves money, reduces costs and reduces waste production, making it possible to obtain high-quality products.

At present, the problem of building particular models and a set of methods of risk assessment and minimization exists in all spheres of human activity. The uncertainty and multi-criteria nature of the areas under consideration, especially the diversity of characteristics stemming from the differences in the assessment and dynamics of the studied objects, create a significant difficulty and obstacles in conducting such a research. Therefore, to link them into a successful model composition is the most difficult task. To date, no fundamental research has been carried out in relation to risk areas, although certain research developments have taken place (Tikhomirov N.P. & Tikhomirova T.M., 2016; Fomin G.P. 2018; DEMIN Sergey S. et al., 2018). Shown that optimal decision making is based on the use of various non-formalized and formalized methods and the degree of their hybridization is determined by different circumstances. It was also indicated that in order to improve the quality of the solution, it is necessary to apply multi-criteria optimization, especially in a situation when the initially selected criteria do not give us full confidence that our final decision is optimal and correct. In that regard, it was pointed out that with approximate estimates of some values obtained by formalized methods it is easier to make a final decision.

Initially, the problem of multi-criteria optimization was raised by the Italian economist V. Pareto in 1904 in the mathematical study of commodity exchange in the trade process (Censor Y., 1977). To cater for this process the sequential concessions method, the ideal point method and the convolution method were suitable. For the purpose of the present study, it is more convenient to use the method based on the convolution of criteria, indicators or characteristics of the object, where instead of a set of specific criteria one scalar criterion obtained by a combination of specific criteria was considered. Among the latter there are multiplicative, additive and mixed methods of convolution of criteria. It is assumed that the criteria are comparable and normalized and their weighted coefficients, which characterize the importance of each criterion among the set, are defined. After that, a new objective function is built and the task of optimization of the scalar criterion is solved (Lootsma F.A. , 1999; Shi-Woei & Lin Ming-Tsang Lu, 2012 ; Kwiesielewicz M., 2004; Gawlik R., 2017). Thus, for example, there is a method of analytic hierarchy process (AHP), first proposed by the American researcher Thomas Saaty (Saaty, T. L. 1980). This method is aimed not only at helping to arrive at the best single decision, but also at ranking possible decisions and criteria used in decision making. Building a decision hierarchy makes possible to carry out comparative assessment of the contributions of alternative solutions and to find the one that best describes a certain ranking criterion and satisfies the conditions of the task (Saaty T. L.  1994; Saaty, T. L. 2012; Koyun Yılmaz S. &  Ozkir V. , 2018). The authors have taken advantage of these methods and combined them into a model composition, integrating them with other mathematical methods used in the process of taking business decisions in manufacturing, selling or buying products under the conditions of uncertainty and conflicting criteria.

It is important to note that the success of commercial activities of any organization is determined by the appropriate formation of the manufactured and sold product range, which is generated on the basis of objective market research, analysis and forecasting demand. In this regard, an important task of the company is to form such a range of products or to prepare an appropriate pre-shipment order, so that they can ensure the optimal allocation of available monetary funds for production or purchase of products with minimal risks.

The subject matter of the research is the mechanisms of formation of risk assessment methods for objects of different nature of business activity in production, selling or buying products under the conditions of uncertainty and conflicting criteria.

Methods of the research include both non-formalized and formalized methods of modeling, principles of system analysis, including structuring and quantification of risk study issues while creating a combined version of multi-criteria methods of optimization. The authors also used statistical methods of ranking the characteristics of the object of evaluation, method of paired comparisons, methods of integral programming, Hungarian method, methods of reduction, method of trial and error.

The purpose of this study is the scientific substantiation and creation of a hybrid method of multi-criteria assessment and minimization of risks in business activities under the conditions of uncertainty. There are economic and mathematical methods which allow to quantitatively justify the choice of solution in conditions of multi-criteria. However, the researchers are interested in a comprehensive method that would consider the opinions of business participants and the characteristics of the object itself, a method that could objectively, justifiably and preferably quickly and simply minimize risks. To this end, we decided to utilize the existing arsenal of both non-formalized and mathematical methods, to integrate their advantages, minimizing their disadvantages and to offer a mixture in the form of a hybrid method of multi-criteria risk minimization. The task of multi-criteria optimization is to search for a vector of objective variables satisfying the given restrictions and optimizing the vector function, the elements of which correspond to the objective functions. Therefore, the task of multi- criteria optimization is reduced to the task of optimization with one scalar objective function. These functions form mathematical description of the criterion of satisfaction and, as a rule, they conflict with each other. That is why it is necessary to find such a solution, at which the value of the objective functions would be acceptable for the problem setter.

This paper proposes methodical approaches and offers practical recommendations on finding an exact solution for a businessman how to ensure the forthcoming demand for a new product and minimize risks at decision-making under the conditions of uncertainty. The authors developed the scientific and methodical substantiation and designed a conceptual economic model of multi-criteria evaluation and risk minimization in the process of product acquisition. Let us consider how a trade organization sets and solves the task by employing in the course of the decision-making a set of necessary methods for assessing risks on buying / selling new products  with the minimum risk under the conditions of uncertain demand. Deviation of revenue from sales in comparison with the expected planned amount determines the risk. In the presented example, it is necessary to make an optimal allocation of monetary funds for the purchase of coffee machines with minimal risk in the formation of product range based on the characteristics presented in Table 1.

Table 1
Comparative characteristics of coffee machines

First, let us find a solution using analytic hierarchy process (AHP). The method of hierarchy analysis includes decomposition using hierarchies and synthesis by finding relationships through experts’ judgments and linear convolution (Saati T.L., 2008; Wang Y. & Luo Y., 2009; Barron F.H., 1992). First, we build a hierarchical structure of the task: goal, criteria, sub-criteria, alternatives. Then, we apply the method of estimation of the strength of judgments (Table 2).

Table 2
Nine-point scale of assessment of the power of judgement

Let us determine the priority vector  for the characteristics using the method of analytic hierarchy process (AHP) in relation to the upper level of the hierarchy. For this purpose, we build a matrix of paired comparisons of coffee machine characteristics (Table 3) and calculate the normalized priority vector for it.

Table 3
Matrix of paired comparisons of coffee machine characteristics

Using this table, we form the square symmetrically reciprocal matrix A:

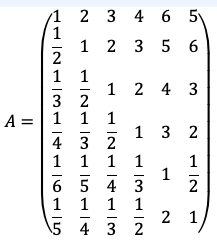
Table 4
Consistency indices for a randomly generated matrix.

The value of a consistency ratio (CR) of 0.10 or less is used as valid value to continue the AHP analysis (Saaty T. L., 1994; Saaty T. L., 2012). If the consistency ratio is greater than 0.10 (CR > 0.1), then this indicates a significant violation of the judgment logic made by the expert when filling the matrix. So, in the case of CR > 0.1, in order to improve consistence the expert is invited to revise his judgment used to construct the judgment matrix. To provide us with an improved judgment matrix with a better consistency, it is necessary to reconsider the data on the properties and characteristics of the products being compared.

In our example above, where n=6, we get CR = 0.0728/1.24= 0.0587. The pair comparison matrix is reasonably consistent because CR <0.1.

Similarly, we calculate the priorities of compared objects in relation to the criteria. Calculation of priority vectors is carried out in the direction from the upper levels to the lower levels, with account for links between elements belonging to different levels.

Table 5
Criterion: Coffee Beans/Ground Coffee.

Let us check the consistency of judgments in the matrix. We have λmax = 6.2 and the size of comparison matrix is 6, thus the consistency index is CI= (6.2-6)/(6-1)= 0.04. Then we have CR=0.04/1.24=0.0323 <0.1. Thus, the comparison matrix is reasonably consistent.

Table 6
Criterion: Coffee Machine Capacity

Let us check the consistency of judgments in the matrix. Since λmax = 6.194, CI=(6.194-6)/6 = 0,0388 and CR = 0.0388/1.24 = 0.0313. The comparison matrix is reasonably consistent because 0.0313 < 0.1.

Table 7
Criterion: Coffee Machine Power

Let us check the consistency of judgments in the matrix. We obtain λmax=6.774, CI= (6.774-6)/5 = ).1555 and CR=0.155/1.24=0.125. The result is negative. Since the consistency ratio is greater than 0.10, this comparison matrix is not reasonably consistent and it is necessary to revise the judgments to locate the cause of the inconsistency and correct it.

Table 8
Criterion: Coffee Machine Power

It turns out that λmax= 6. Hence, CI = 0 and CR=0/1.24=0. In this case we have an ideal judgment matrix, i.e. the matrix is completely consistent.

Table 9
Criterion: Coffee Machine Height.

Let us check the consistency of judgments in the matrix: λmax=6.153, CI=(6.153-6)/5 = 0.036 and CR=0,0306/1.24 =< 0.1. Therefore, the comparison matrix is reasonably consistent.

Table 10
Criterion: Weight.

We have λmax=6.433 and, consequently,CI = (6.433-6)/5 = 0.0866; CR=0.0866/1.24=0.0698. Since this value of 0.0698 for the consistency CR is less than 0.10, the comparison matrix is reasonably consistent.

We carry out a hierarchical synthesis. We consistently define the vectors of priorities of alternatives concerning the elements of the hierarchy at all hierarchical levels.

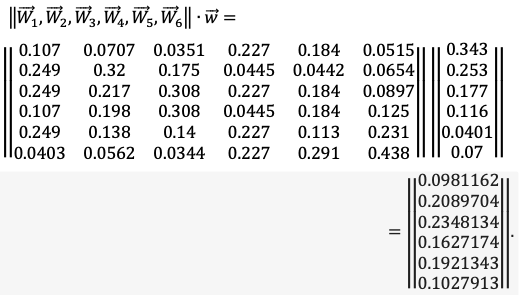
As a result, generalized weight coefficients of each coffee machine model were determined. Let us rank them in descending order of their generalized priorities: 1. Saeco (0.235); 2. Siemens (0.209); 3. Bosch (0.192); 4. Philips (0.163); 5. Nespresso (0.103); 6. Melitta (0.098).

Now we will apply different combined methods to solve the same problem on search of the optimal decision ensuring risks minimization in business decision-making process in manufacturing, selling or buying products in the conditions of uncertainty and conflicting criteria. Comparing the characteristics of coffee machines, we build a matrix of paired comparisons (Table 11), the elements of which are determined by the following rule:

Table 11
Paired Comparison Matrix of Characteristics.

Table 12
The scoring assessment of coffee-machine characteristics

Using the data from this table we determine the values of integral evaluations of coffee machine quality without taking account of the price by the following formula:

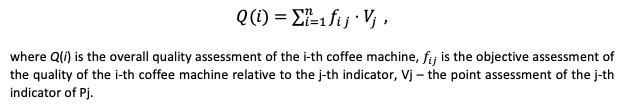
In matrix form, the calculation of general priorities is written as follows:

Optimal allocation of monetary funds on formation of optimal product range with the minimum risk should be carried out in quantities and shares defined after rationing operation.

Table 13
Allocation of Funds with Minimal Risk.

We consider that under conditions of uncertainty and unclear consumer demand, the level of comparison to determine the risk is the uniform distribution of allocated funds in the amount of 1 million rubles in equal shares Qun. = 1/6 = 0.167. It should be noted that the price of purchase accounts for about 50% of the selling price. The ratio of integral quality characteristic, for example, for Q(Saeco) = 4.31 to the total sum of qualities ∑Q(i) = 19.82 determines the share of the allocated amount with the minimum risk for the purchase of Qopt. = 4.31/19.82 = 0.217. Accordingly, the risk of lost profit (R1) will be determined by the difference 0.217 – 0.167=0.05, i.e. R1 = 5%. Similar calculations have been performed for all brands of coffee machines and are presented in Table 13. On the basis of these calculations, the Pareto diagram can be completed. In general, the risk of loss of profit will constitute 11.2%, and the risk of frozen funds will amount to (11.5%), which is also a part of the lost risk and makes up 11.2%+11.5% = 22.7% of the allocated funds, i.e. 445 thousand rubles, which is quite essential for their further turnover. In order to minimize risks, it is necessary to distribute funds based on the Pareto diagram. Thus, the existing formalized methods of risk assessment based on the results of risk identification and the identification of risk indicators can be used in combination with mathematical methods to conduct a risk assessment, but this process requires a great deal of expertise and extensive knowledge of risk theory.

It should be noted that the weight of the indicators in the paired matrix of characteristics in the hybrid method and AHP almost coincide. Calculation of the correlation relationship between weights of criteria, which were calculated in both methods, found that there is a strong correlation between them (0.95). However, it should be noted that the solution of the problem by the AHP method and the hybrid method still gives a discrepancy, because the ranked lists of coffee machines do not coincide. This is due to the fact that the application of the nine-point scale for estimation of the power of judgments does not allow using it successfully and accurately in the presented variant, as there is no binding of numerical values of characteristics to the scale points. Therefore, it is necessary to create a special interval scale with reference to the number of product characteristics, and the scale must be observed for all characteristics. Our ability to do so depends heavily on the factors that we can measure in order to compare. The analysis of the strengths and weaknesses with the method of the analytic hierarchy process has shown that the use of a scale from 1 to 9 increases the degree of sensitivity, but is highly dependent on the expert. Calculation of the consistency index helps avoid violations in the experts' logic regarding the importance (significance) of the indicators and criteria, however, this did not work out when solving the problem by this method and other evaluation criteria are obviously needed. In general, the AHP method is complex and time-consuming to use, especially when increasing the number of characteristics, for example, up to 10. The scale is intermittent. It should be modified to adjust the interval scale to the physics, the nature of the task. To find out the significance of the criteria, an interval scale with quantitative grading of characteristics and a matrix of paired comparisons should be used, which is the easiest for the experts to perceive. Analyzing and using the advantages of different methods and eliminating disadvantages, we have developed a hybrid method of multi-criteria risk minimization, which is easy enough to solve the problems of multi-criteria optimization, because it takes much less time to solve the problem. Thus, the existing non-formalized and formalized methods of risk assessment based on the results of risk identification and identification of risk indicators can be used in a rich combination with mathematical methods to assess and minimize risks, but this process requires expertise, extensive knowledge and involvement of specialists of different profiles.

The scientific-methodical substantiation of the hybrid method of multi-criteria evaluation was carried out and the authors offered conceptual model of minimization of risks of various products, suitable for use in various spheres of entrepreneurial activity. The model includes as a basis the principles of system analysis – structuring and quantification of the risk study issue, creation of the combined version of multi-criteria method of optimization. Development of methodical and practical recommendations has been carried out on a specific example of risk assessment and minimization. The proposed methods and tools allow for the assessment and consideration of possible risks at all stages of the search for solutions for the production, manufacture or purchasing various products to avoid adverse economic consequences in business activities.

Alonso J. A. , Lamata M. T.  (2006)  Consistency in the analytic hierarchy process: a new approach. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems. Vol. 14, number 4, pp.445−459.

Barron F.H. (1992). Selecting a Best Multiattribute Alternative with Partial Information about Attribute Weights. Acta Psychologica. Vol. 80, pp. 91-103.

Belton V., Stewart T. (2002). Multiple Criteria Decision Analyses: An Integrated Approach. Boston: Kluwer Academic Publishers. DOI 10.1007/978-1-4615-1495-4.

Censor Y. ( 1977). Pareto Optimality in Multiobjective Problems. Applied Mathematics and Optimization, Vol. 4, pp. 41-59.

Chistyakova N.A., Sukhorukova I.V (2018). Methodical Aspects of Actuarial Mathematics Teaching.  Astra Salvensis Vol.VI , Special Issue, pp. 847-857.

DEMIN Sergey S., DOMBROVSKAYA Elena N., Mushrub Vladimir A., Shichiyakh Rustem A., Gaponenko Tatiana V. (2018). Essence and the impact of risks and uncertainties in the investment-related decision-making process. Revista Espacios. Vol. 39, year2018, number 31, page 13. Retrieved from: https://www.revistaespacios.com/18393113.html.

Gawlik R., Głuszak M., Małkowska A. (2017). Folia Oeconomica Stetinensia. The Journal of University of Szczecin, Vol. 17, Issue 1, pp. 31–43.

Fomin G. P. (2018). Formal methods of risk assessment in trade. Collection of scientific papers "Herald of Plekhanov Russian Economic University", Vol. 5, pp. 101-107.

Hesham K.A., Salih O.D. (2008). Assigning Cardinal Weights in Multi-Criteria Decision Making Based on Ordinal Ranking. Journal of Multi-Criteria Decision Analysis, Vol. 15, рp. 125-133.

Horn, R.A. , Johnson C.R., (2013) Matrix Analysis. Cambridge University Press, 643p.

Kwiesielewicz M., van Uden E. (2004). Inconsistent and contradictory judgements in pairwise comparison method in the AHP. Computers & Operations Research, Vol.31, No5, pp. 713–719.

Koyun Yılmaz S., Ozkir V. (2018). Extended consistency analysis for pairwise comparison method. International Journal of the Analitic Hierarhy Process. Vol 10, number 1, pp. 160-176.

Lootsma F.A. (1999). Multi-Criteria Decision Analysis via Ratio and Difference Judgement. Dordecht: Kluwer Academic Publishers.

Saaty T.L. (1980). The Analytic Hierarchy Process. McGraw-Hill International, New York.

Saaty T.L. (1994). Fundamentals of Decision Making and Priority Theory with the Analytic Hierarchy Process. RWS Publications, 527 p.

Saaty T.L. (2008). The Analytic Hierarchy and Analytic Network Measurement Processes: Applications to Decisions under Risk. European Journal of Pure and Applied Mathematics, Vol.1, No. 1, pp. 122-196.

Saaty T.L. (2012). Decision Making for Leaders: The Analytic Hierarchy Process for Decisions in a Complex World. Third Revised Edition. Pittsburgh: RWS Publications.

Shi-Woei Lin, Ming-Tsang Lu. (2012). Characterizing disagreement and inconsistency in expert’s judgments in the analytic hierarchy process. Management Decision, Vol. 50, Issue 7, pp.1252-1265.

Sukhorukova I.V., Chistyakova N.A. (2018). Optimization of the Formation of the Capital Structure of the Insurance Company, Taking into Account the National Specifics of Insurance. Journal of Reviews on Global Economics, Vol. 7, pp. 146-151.

Tikhomirov N.P., Tikhomirova T.M. (2016). Risk of analysis and economic. Publishing "Economics", Moscow, 117 p.

Wang Y., Luo Y. (2009). On Rank Reversal in Decision Analysis. Mathematical and Computer Modelling, Vol. 49, P. 1221-1229.

1. Doctor of Economic Sciences, Professor. Plekhanov Russian University of Economics, Moscow, Russia. Contact e-mail suhorukovaira@yandex.ru

2. Candidate of Technical Sciences (Ph. D.), Professor. Plekhanov Russian University of Economics, Moscow, Russia. Contact e-mail gpfomin@mail.ru

3. Candidate of Historical Sciences, Head of the Department of Foreign Languages, Professor. Plekhanov Russian University of Economics, Moscow, Russia. Contact e-mail irinaekareva@mail.ru

4. Candidate of Science in Physics and Mathematics, Associate Professor. Plekhanov Russian University of Economics, Moscow, Russia. Contact e-mail mushrub@yandex.ru