

 Vol. 40 (Nº 26) Año 2019. Pág. 1
Vol. 40 (Nº 26) Año 2019. Pág. 1
MANRIQUE, Nelcy J. 1; GALLO, Ashley M. 2 y PRADA, Raúl 3
Recibido: 21/08/2018 • Aprobado: 07/07/2019 • Publicado 29/07/2019
RESUMEN: En esta investigación se implementó la ingeniería didáctica como metodología de investigación la cual fue presentada por Artigue y Douady en Colombia en el segundo simposio internacional en educación matemática. Este trabajo pretendía abordar el diseño y la evaluación de intervenciones educativas basados en la investigación para mejorar la enseñanza y el aprendizaje del cálculo. Se diseñaron secuencias didácticas apoyadas en las teorías de las situaciones didácticas y de las representaciones semióticas que pretendían la correcta apropiación del concepto de función en un grupo de estudiantes de Licenciatura en Matemáticas. Los resultados evidenciaron beneficios en el proceso de apropiación conceptual. |
ABSTRACT: In this research, didactic engineering was implemented as a research methodology which was presented by Artigue and Douady in Colombia at the second international symposium in mathematics education. This paper aimed to address the design and evaluation of educational interventions based on research to improve the teaching and learning of calculus. Didactic sequences were designed based on the theories of didactic situations and semiotic representations that sought the correct appropriation of the concept of function in a group of students with a Bachelor's degree in Mathematics. The results showed benefits in the process of conceptual appropriation. |
“El concepto de función es uno de los más difíciles tanto para su enseñanza como para su aprendizaje” y a partir de esta afirmación no se puede pretender que un estudiante tenga total apropiación del mismo por medio de una clase expositiva tradicional según lo afirmado por Eisenberg (1991), siendo este uno de los principales problemas que se presentan en la educación debido a que es un concepto básico para el aprendizaje del Cálculo. Diversas investigaciones de Educación Matemática (Benítez, 2010; D`Amore, 2006; Eisenberg, 1991; Fabra y Deulofeu, 2000; López y Sosa, 2008; Prada, Hernández y Ramírez, 2016) han analizado las dificultades que presentan los estudiantes en la construcción de este concepto y en las problemáticas que ha traído la enseñanza de técnicas de solución que permiten resolver ejercicios y problemas estandarizados del concepto de función en el proceso educativo.
Para el Ministerio de Educación Nacional-MEN (2005) el conocimiento matemático se distingue por dos tipos: el conocimiento conceptual y el conocimiento procedimental. El primero se prioriza por lo teórico y la reflexión, producido por la actividad cognitiva, se relaciona directamente con el saber qué y el saber por qué. Por otro lado, el procedimental se enfoca en la habilidad para elaborar, relacionar y comparar algoritmos; basado en la acción para representar conceptos por medio de estrategias y técnicas. Estos conocimientos van de la mano uno del otro, siendo el conceptual la base y el procedimental el complemento que ayuda a la construcción y el entendimiento de los conceptos por medio del contexto y su uso eficaz. De esta forma el conocimiento procedimental se relaciona con el saber cómo (MEN, 2005, p.50). Sin embargo, en COLOMBIA el proceso de enseñanza y aprendizaje de las Matemáticas en la Educación Básica Secundaria y Media, se sigue enfocando más en el conocimiento procedimental donde se le da prioridad a la mecanización (Herrera, Montenegro y Salvador, 2011). Tal como lo afirma Hitt (2003) la mecanización es el principal inconveniente que presentan tanto docentes como estudiantes para desarrollar un total entendimiento del concepto; al restringirse a una manipulación algebraica relativa del concepto se produce una limitación en su comprensión, generando en los estudiantes habilidades de solución pero con un patrón estandarizado limitando el análisis y la comprensión del concepto, haciendo un distanciamiento entre su comprensión a nivel escolar y su utilidad en diversas situaciones de la cotidianidad, tal como se resalta en Villa y Ruiz (2011).
El aprendizaje de las matemáticas es un proceso que involucra actividades cognitivas como el razonamiento, la resolución de problemas, la comprensión de texto y la conceptualización. Estas actividades según Duval (2012) para la enseñanza y el aprendizaje de las matemáticas requieren además del lenguaje natural y las imágenes la utilización de los diferentes registros de representaciones semióticas. Duval (citado en Guzmán, 1998) afirma que “las representaciones semióticas son aquellas que su producción no puede realizarse sin la movilización de un sistema semiótico; así las representaciones semióticas pueden ser producciones discursivas (en lenguaje natural, en lenguaje formal) o no discursivas (figuras, gráficos, esquemas, entre otras)”.
Según Duval (1999) todo conocimiento está sujeto a una actividad de representación, es decir, que cuando en el proceso de enseñanza se recurre a la utilización y articulación de diferentes registros de representación (gráfico, algebraico, tabular, lengua natural, diagrama sagital, entre otros) el aprendizaje del concepto resulta favorecido. Para Duval (2012) en la comprensión del concepto se necesita que por lo menos se haga uso de dos registros, y que además se hagan transformaciones coherentes de una representación a otra sin ni siquiera estar conscientes de ello. EL uso de las representaciones semióticas en el proceso de enseñanza es de igual forma importante para comprender el concepto de función (Amaya de Armas y Sgreccia, 2014). Como lo afirma Duval (2004) una de las dificultades que se presentan en el aprendizaje de las Matemáticas es la transformación entre los diferentes registros de representación, es decir, identificar elementos pertenecientes a un registro de partida y encontrar su equivalente en el registro de llegada. “De esta forma la enseñanza del concepto de función no se puede reducir a una explicación tradicional” Hitt (2003), donde el docente parte del concepto para posteriormente proponer una expresión algebraica a partir de la cual realiza su respectiva tabulación y su gráfica en el plano cartesiano. La anterior secuencia de enseñanza es la predominante en Colombia en el sistema educativo (Herrera, Montenegro y Salvador, 2011). Lo que desencadena en una limitación conceptual puesto que los estudiantes mecanizan este proceso sin acompañarlo de un adecuado razonamiento.
EL concepto de función es uno de los conceptos básicos en la enseñanza y aprendizaje del Cálculo tal como se resalta en las investigaciones realizadas por Benítez (2010), DʹAmore (2006), Sánchez-Matamoros, García y Llinares (2008), Hernández, Prada y Ramírez (2017), entre otros. Al ser este concepto indispensable para el aprendizaje del cálculo se hace necesario que los estudiantes tengan total apropiamiento del mismo para que al momento de ingresar a la Educación Superior puedan avanzar por los diversos cursos de cálculo sin tener demasiada dificultad.
Tal como se menciona en Prada, Hernández y Ramírez (2016) las dificultades presentadas por los estudiantes vienen dadas por la tendencia de los docentes a no considerar como fundamental la construcción del conocimiento matemático, a partir de la conexión de las diferentes representaciones del concepto de función como el gráfico, algebraico, tabular, lengua natural, diagrama sagital, entre otros; por lo que la principal dificultad en los estudiantes se presenta es el tránsito entre los diferentes tipos de representación (Hitt, 2003; Duval, 2004; Sureda y Otero, 2013). Siguiendo ésta misma línea argumentativa, en Flores y Cázarez (2004) se afirma que “los programas de matemáticas de la educación media y superior, principalmente para quienes estudiarán ciencias, ingeniería o contabilidad, prevén el que los estudiantes puedan analizar funciones incluso usando los criterios asociados a la derivada”. Aspecto que sin duda no sucede en los colegios, por lo que en la mayor parte de los casos cuando inician la educación superior en su primer curso de Cálculo, los estudiantes tienen dificultades en el momento de abordar contenidos como límite, continuidad o derivada (Prada, Hernández & Ramírez, 2016). Por todo lo mencionado, es evidente que la escasa comprensión del concepto de función que poseen los estudiantes al ingresar a la educación superior se convierte en una dificultad para aprobar el curso de Cálculo Diferencial, siendo uno de los cursos que más problemáticas presenta en los estudiantes universitarios por la falta de compresión de los conceptos fundamentales (Fiallo y Parada, 2014, p.57).
Todas estos problemas encontrados a nivel de educación básica media y educación superior mencionados en los antecedentes investigativos fueron contrastadas con los estudiantes de primer semestre del programa académico de Licenciatura de Matemáticas de la Universidad Francisco de Paula Santander-UFPS destacando que muchas de ellas se presentaban con frecuencia, por lo que se hace necesario elaborar un plan de acción que al intervenir pedagógicamente genere cambios en el proceso de enseñanza y aprendizaje del concepto de función. Basados en las problemáticas mencionadas anteriormente y buscando que los estudiantes tengan total apropiación del concepto de función, se elaboran secuencias didácticas enmarcadas dentro de las teorías de las situaciones didácticas de Brousseau que describe el proceso de producción de conocimientos matemáticos en una clase a partir de dos tipos de interacciones: 1) la interacción del alumno con un medio que ponga a prueba lo que sabe o que le permita conocer nuevos saberes , llamada teóricamente como intencionalidad didáctica y 2) la interacción con el docente conocida como contrato didáctico. Brousseau (citado en Sadovsky, 2005)
stas secuencias también se encuentran bajo las representaciones semióticas de Duval, que se apoyan en la ingeniería didáctica como método de investigación. Donde por medio de la observación, realización y análisis de las secuencias de enseñanza permite llevar un informe detallado de los efectos que han tenido los estudiantes desde el inicio de la intervención (Artigue, Douady y Moreno, 1995) haciendo en primer momento un recorrido epistemológico del concepto y las concepciones presentadas por los estudiantes y docentes alrededor del mismo, además de indagar en el campo de la enseñanza tradicional y sus efectos generados en la educación. En un segundo momento se contrasta las problemáticas encontradas con la población a intervenir, a partir de un análisis a priori que consiste en una prueba inicial la cual determina el camino a seguir para la elaboración de secuencias didácticas que ayuden a superar las dificultades expuestas. Como lo define Tobón, Pimienta y García (2010) las secuencias didácticas son “conjuntos articulados de actividades de aprendizaje y evaluación que, con la mediación de un docente, buscan el logro de determinadas metas educativas, considerando una serie de recursos” (p.20). Con la implementación de estas secuencias didácticas se espera que pueda generar un efecto positivo en el proceso de aprendizaje de los docentes en formación enfocados a abordar los diversos aspectos asociados con el concepto de función.
Se desarrolló una investigación cuasi-experimental haciendo uso de la estrategia longitudinal (Fernández, Vallejo, Livacic y Tuero, 2014), dónde se manipuló el método de enseñanza con el fin de analizar su efecto en el proceso de aprendizaje, observando el comportamiento de los integrantes de la muestra, en el desarrollo de actividades relacionadas al Cálculo Diferencial.
Se realizó un análisis inicial de las dificultades que habitualmente se presentaron alrededor del concepto de función, derivado de la construcción del estado del arte, fase que se desarrolló como punto de partida a esta investigación. Toro, Jaramillo y Parra (citado en Vargas, Higuita y Muñoz, 2015) definen el estado del arte como la revisión de antecedentes, proponiéndolo como un momento metodológico dentro de cualquier investigación que busca clasificar el estado actual de un problema .A partir de esta construcción y análisis, se encontró que una de las principales dificultades, es que los estudiantes memorizan la definición de función pero no poseen la capacidad de reconocer o identificar funciones en diversos registros de representación (Manrique, Gallo y Prada, 2017). De forma complementaria, se hace evidente la dificultad para articular de forma coherente diversos registros de representación de una función, llevando a que no se alcance una correcta apropiación del concepto dado que se considera, que un estudiante entiende el concepto de función cuando logra hacer aplicaciones de éste y al mismo tiempo hace articulaciones coherentes en los diferentes registros de representación semiótico. Como lo afirma Duval (citado en Manrique, Gallo y Prada, 2017) “lograr que un estudiante haga transformaciones coherentes entre los diferentes registros de representación hace que se apropie del concepto”.
Se adoptó la metodología de ingeniería didáctica aplicando cada una de las etapas que proponen sus autores:
Artigue, Douady y Moreno (1995) plantea cuatro fases de la metodología de ingeniería didáctica.
La fase 1, de análisis preliminar: Se realiza el análisis epistemológico de los contenidos contemplados en la enseñanza, que atienda a las dificultades presentadas por estudiantes alrededor del concepto de función.
La fase 2, la concepción y análisis a priopri, se describen y se predice lo que el estudiante va a realizar en la experimentación. Realizando unas actividades pre-instruccionales que consisten en el diseño y aplicación de un instrumento diagnóstico a fin de identificar los conocimientos previos.
La fase 3, experimentación, se aplican secuencias didácticas que se diseñan teniendo en cuenta el análisis a priori. Creando una serie de actividades para trabajar sobre las dificultades encontradas alrededor del concepto de función.
Finalmente, la fase 4 de evaluación y análisis a posteriori: Se apoya en todo el proceso realizado en la experimentación donde, finalmente se compara los resultados obtenidos en el análisis a priori y el análisis a posteriori.
Para el desarrollo de la investigación se proponen tres tipos de instrumentos: test diagnóstico, intervención de secuencias didácticas y test final. Para la construcción del instrumento diagnóstico se apoyó en un grupo focal integrado por cinco docentes que han orientado el curso de Cálculo Diferencial en los últimos cuatro semestres de forma ininterrumpida en programas académicos de las diferentes facultades de la UFPS. Se pretendía con ello obtener un panorama general del problema. Como producto de esta actividad se identificaron una serie de pre-saberes asociados con los pensamientos numérico y variacional que a juicio de los participantes impiden el correcto entendimiento del concepto de función, dentro de los que se destacan: operaciones con diversos conjuntos numéricos y su evaluación en expresiones algebraicas, concepto de plano cartesiano y de par ordenado, reconocimiento de los ejes por diversos nombres y cómo ellos generan los diversos cuadrantes. La aplicación del instrumento fue sin previo aviso y la duración fue de noventa minutos, en donde contestaron sin ningún apoyo tecnológico ni bibliográfico. Las valoraciones fueron analizadas bajo la metodología cuantitativa. Posteriormente, se diseñó una serie de actividades en las que se buscaba que los participantes estuvieran inmersos en la solución de secuencias didácticas fundamentadas en la articulación de diversos registros de representación semiótica, con el fin de que se apropien del concepto de función bajo el uso de representaciones semíticas, logrando la articulación de diversos registros de representación. Las actividades buscan que el estudiante mejore sus habilidades en la identificación de diferentes funciones reales, analizando gráficos y sus principales características tales como dominio y rango, entre otros aspectos.Terminadas las intervenciones pedagógicas se aplicó la prueba final la cual constaba de varios ítems en los que se incluyeron actividades como: identificación de función a nivel gráfico y analítico; a partir de la gráfica identificar dominio, rango, intervalos dónde crece o decrece la función, existencia de asíntotas, clasificar el tipo de función para intentar proponer una expresión algebraica asociada a la misma; a partir de la expresión algebraica determinar de forma analítica el dominio, el rango, la presencia de asíntotas, si la función es biyectiva como criterio para determinar si tiene inversa, entre otros aspectos; resolver situaciones en contextos en dónde se aplica la modelización de funciones.
La población está integrada por la totalidad de estudiantes matriculados en el programa académico de Licenciatura en Matemáticas de la UFPS durante el primer semestre de 2018.
Se recurrió al muestreo no probabilístico bajo la técnica de muestreo intencional, dado que el interés era analizar el grupo de estudiantes que egresan del sistema de educación secundaria y hacen su paso a la educación superior, siendo el curso de Cálculo Diferencial el primero de los cuatro cursos de cálculo que deben superar en su proceso de formación académica. Se logró conformar un tamaño de muestra de 25 estudiantes de ambos géneros, con predominio del género femenino. Sus edades oscilan entre los 16 y 19 años, donde el 90% de los participantes son estudiantes recién egresados de la educación media y el restante son estudiantes repitentes del curso.
La presentación de los resultados se realiza de acuerdo a cada una de las etapas desarrolladas en la investigación y que están enmarcadas dentro de la ingeniería didáctica.
La prueba diagnóstica consistió en una revisión de conocimientos previos necesarios para el desarrollo del concepto de función. La prueba inicia con la realización de algunas operaciones básicas utilizando diversos conjuntos numéricos en dónde se pone en evidencia que aproximadamente el 95% de los evaluados presentan dificultades en el manejo de los números racionales en sus diversos formatos (como fracción, como decimal o en el caso de fracciones impropias, como número mixto). Con respecto al reconocimiento de los ejes del plano cartesiano, se evidencia un desconocimiento por parte del 44% de estudiantes cuando se utilizan expresiones como abscisa u ordenada, lo que los lleva a desconocer su relación con los llamados ejes “x” y “y”, aspecto que se reflejaba en un intercambio de los ejes cada vez que se les llamó con esos nombres en el 52% de los casos. En lo que respecta a la ubicación de parejas ordenadas en el plano cartesiano, el 90% de ellos lo hacen correctamente a partir de las parejas ordenadas, pero al cambiar el formato de enunciación empiezan a evidenciarse las dificultades, por ejemplo, ante la expresión “4 unidades en el eje negativo de las ordenadas y 3 unidades en el eje positivo de las abscisas” produjo que el 36% de los estudiantes ubicaran de forma inadecuada los puntos. Posteriormente, se proporciona una lista de parejas ordenadas las cuales debían identificar el cuadrante en que se ubicaban, obteniendo el 72% de los aciertos en este caso. finalmente, se cierra la prueba con un enunciado de una situación cotidiana que podía modelarse como una función entre dos variables, para lo cual se les pedía que construyeran una tabla de valores que evaluara diversas situaciones del enunciado, es decir, los estudiantes debían articular dos registros de representación de una función (del registro en lenguaje natural al registro tabular). Se encontró que el 84% de los estudiantes realizan la tabla de valores identificando adecuadamente la relación entre las variables, pero sólo el 48% de ellos logran contextualizar los valores empleados de forma que garanticen el sentido del problema.
Con base en los resultados obtenidos en la prueba inicial, en los antecedentes consultados y en lo comentado por los docentes en el grupo focal, se elaboraron las diversas secuencias didácticas las cuales se trabajaron en cinco sesiones de 120 minutos. Las actividades incorporadas en cada secuencia didáctica fueron propuestas o seleccionadas por los investigadores y antes de ser aplicadas fueron socializadas a los integrantes del grupo focal de docentes, quienes apoyaron el proceso de validación como expertos.
En cada sesión se les presenta la actividad a realizar y se les proporciona un espacio de 90 minutos para resolver las situaciones presentadas en grupos de tres estudiantes cada uno, finalizando con la explicación del docente a partir de lo realizado al interior de cada grupo de trabajo. De esta forma se recurre al aprendizaje cooperativo como recurso de apoyo en el aula. Cabe resaltar que en cada sesión se hace énfasis en un tipo de representación y a partir de ella se le pide al estudiante hacer transformaciones coherentes a otros registros de representación. De igual forma se trabajan en el reconocimiento de los diferentes tipos de funciones.
En la primera sesión se trabaja en la definición de función, partiendo con la pregunta “para usted y de acuerdo a lo estudiado en el colegio ¿qué es función?” al realizar esta pregunta inicialmente, las respuestas de los participantes permiten tener un punto de referencia para la solución acertada y coherente de los demás ítem. La dificultad observada es que aproximadamente el 90% de los participantes replicaron la siguiente definición: “una función es una relación donde cada elemento del conjunto de partida se asocia con solo un elemento del conjunto de llegada”. El porcentaje restante de los participantes expresaron no saber del tema.
El segundo ítem parte de la pregunta ¿qué es función? los participantes debían analizar diversas opciones de respuesta, las cuales debían transformarlas en expresiones algebraicas que les permitiera evaluar su validez. Al analizar las respuestas de los estudiantes se pudo evidenciar que en el momento de generar la expresión algebraica presentaban inconvenientes para distinguir la variable dependiente e independiente. Además, para decidir si era o no función, los participantes hacen un proceso mecánico se limita al proceso de tabular para posteriormente hacer la ubicación de puntos en el plano cartesiano y trazar la gráfica mediante la unión de los puntos. En las siguientes situaciones propuestas, se busca que los estudiantes identifiquen funciones a partir del registro gráfico para posteriormente intentar proponer su expresión algebraica. Cuando analizan las gráficas los estudiantes utilizan el criterio de la línea vertical para verificar si corresponde a una función. Para cumplir con el objetivo de proponer la expresión algebraica asociada a la gráfica, recurren a la ecuación punto pendiente en el caso de funciones lineales y en las demás funciones, no logran proponer una expresión asociada a la gráfica.
En esta sesión se trabajó la representación de funciones a partir del registro gráfico. Se inicia con una actividad de apareamiento en dónde por un lado se tienen representaciones gráficas en el plano cartesiano de diversas funciones y en la otra columna, se tiene una lista de las funciones reales.
En el segundo ítem se inicia con la definición de funciones inyectiva, sobreyectiva o biyectiva. Posteriormente, se les proporciona la expresión algebraica de varias funciones, a partir de ellas deben generar su representación gráfica en el plano cartesiano, para finalizar con el análisis de cada una de ellas que finaliza con su clasificación en alguna de estas tres funciones ya mencionadas. Estos conceptos son tratados desde la educación secundaria, sin embargo, los estudiantes expresan no conocer del tema mencionado, afirmaban que es la primera vez que los escuchan, decidieron apoyarse en algunos compañeros que sí entendían para que les explicaran, haciendo uso del trabajo cooperativo.
Las siguientes situaciones se establecieron para el análisis de gráficas determinando los intervalos de crecimiento y decrecimiento de las funciones. Aspecto que se complementó proporcionando diversas características de la función en la que los participantes debían proponer la representación gráfica que cumpliera con todas ellas de forma simultánea. Se destaca que los participantes en estas actividades fueron muy acertados en sus argumentos.
En esta sesión se dedicó toda la actividad a la articulación entre los registros de representación en lenguaje natural y el registro de representación algebraico de funciones, para lo cual se inicia con una serie de situaciones cotidianas en dónde se definen situaciones entre variables que requerían ser expresadas como una expresión algebraica. Esta actividad les generó grandes dificultades a los participantes, ya que aproximadamente el 86% de ellos se les dificultó identificar las variables dependiente e independiente, para luego proponer su relación por medio de una expresión algebraica. En la segunda parte de la actividad, se propuso el proceso inverso, en el que se les proporcionaron diversas expresiones algebraicas y los participantes debían proponer enunciados en los que se relacionaran variables presentes en diversos contextos cotidianos. Vale la pena resaltar que el tema de funciones a tramos o por partes, ha generado en los participantes, dificultades ya que en ellos está presente la concepción de que para ser función debe tener una sola expresión algebraica para todos los valores del dominio. Vale la pena resaltar que a medida que se avanza en el desarrollo de las diversas sesiones, se consolida el trabajo cooperativo entre los participantes, se evidencia que van perdiendo el temor a participar o a expresar sus opiniones puesto que reconocen que es el aula un espacio de aprendizaje continuo y sus compañeros son parte del proceso.
La cuarta sesión se hizo énfasis en la articulación entre los registros de representación algebraico al gráfico haciendo énfasis en la identificación del dominio y el rango de las funciones. La primera situación planteada consiste en determinar el dominio y rango de funciones a partir de su representación gráfica. Los participantes logran relacionar el eje de la “x” como el conjunto universal asociado a los valores del dominio y el eje “y” con el conjunto del cual se obtiene el rango. En la segunda situación propuesta se les solicitó relacionar los valores de dominio y rango con su respectiva función. Se destaca que las funciones a tramos acá ponen en evidencia otra concepción presente en los participantes y es el hecho de que, al no ser continúas en su trazo, no son funciones. Se destaca que manifiestan haber escuchado la palabra “asíntota” pero no saben que es. En la tercera situación se les presenta una gráfica y a partir de esta, se busca que los participantes determinen la expresión algebraica e identifiquen los elementos que pertenecen al dominio y cuáles de las opciones dadas podrían ser su imagen. Aproximadamente el 36% de los participantes respondieron correctamente, sin embargo, solo seleccionaron lo que les proporcionaba la gráfica ignorando que su dominio y rango era infinito por ser una línea recta.
la actividad concluye con la cuarta situación donde se les proporcionan expresiones algebraicas con las que se busca que los participantes haciendo uso de su habilidad mecanicista logren algebraicamente obtener tanto el dominio como el rango de la función para posteriormente representarla en el plano cartesiano.
En la última sesión se maneja el concepto de función inversa para lo cual se utilizan diversos registros de representación en el primer ítem se les pidió a los participantes escribir las tres condiciones que se necesitan para determinar si una función es inversa. Con el respectivo análisis se pudo comprobar que más del 90% de ellos desconocen el concepto de función inversa. En el segundo ítem a partir de expresiones algebraicas y aplicando lo que escribieron en el ítem anterior primero debían hallar la inversa de las funciones si era posible. Muy pocos participantes lograron hallarla por la dificultad ya mencionada, lo que obligó a interrumpir la dinámica de trabajo ya definida, para abrir un espacio de reflexión en el que el docente investigador socializó el tema para así retomar el trabajo propuesto. Con el fin de observar la articulación de diferentes registros se realizó el siguiente ítem donde se les proporcionó a los participantes la tabulación de una función y ellos debían expresarla en registro gráfico y algebraico, para finalizar con su inversa, en caso de ser posible. Se pudo evidenciar que los participantes hicieron la articulación de registros correctamente, pero muy pocos lograron hallar la inversa. La dificultad aumentó en el momento de incorporar funciones a tramos. Por último, se les pidió a los participantes que, a partir de unas funciones representadas gráficamente, hallaran la representación gráfica de su función inversa. Se resalta que menos del 30% de los estudiantes propusieron una representación acertada ante lo solicitado.
Finalizado el proceso de intervención en aula, se aplicó una prueba que permitió analizar los efectos que se dieron a partir de la aplicación de las secuencias didácticas, en torno a las dificultades presentadas por los participantes alrededor del concepto de función. La prueba se enfocó principalmente en el reconocimiento de funciones en cualquier tipo de registro de representación semiótica.
La prueba estaba conformad por cinco ítems, donde se pudo medir la articulación coherente de los diversos registros de representación. En el primer ítem del instrumento se proponían cuatro representaciones gráficas de las cuales, una era una parábola con eje principal paralelo al eje horizontal. Los participantes debían identificar en cada gráfica si representaba o no una función. En caso afirmativo, debían mencionar el domino y el rango.
Figura 1
Identifica funciones a
partir del registro gráfico

De los resultados obtenidos se evidencia que el 84% de los participantes seleccionaron adecuadamente las funciones apoyados en el criterio de la recta vertical. El porcentaje restante, afirman que toda parábola es una función y para tal fin dicen que es función bajo el criterio de la recta horizontal. Se puede observar en estos cuatro participantes que, para justificar su selección, no tienen problema para modificar la orientación de la recta vertical sin dimensionar el efecto que ello tiene en la construcción de parejas ordenadas.
Debido a la dificultad encontrada por parte de los estudiantes con el lenguaje cotidiano se formula el segundo ítem, donde se les presenta un enunciado, con lo cual se buscó que generaran una expresión algebraica.
Figura 2
Identifica funciones a partir del
registro del lenguaje cotidiano
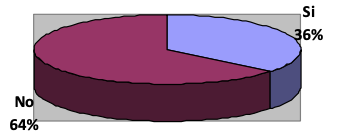
De los resultados se evidenció que un 64% de estudiantes presentan dificultades al analizar un enunciado, su actividad cognitiva de razonamiento y comprensión de texto les impidieron dar solución y hacer la respectiva transformación de registro. El porcentaje restante, que corresponde a 9 estudiantes afirman que el enunciado presentado es una función y además plantean la expresión algebraica correcta.
El ítem tres propone ciertas características de dominio y rango enunciados a través de la notación de conjuntos. Para lo cual el participante debía elaborar una representación gráfica en el plano cartesiano que cumpliera con las características dadas.
Figura 3
Representa funciones en el registro
gráfico a partir de su dominio y rango

De los resultados obtenidos se evidencia que un 96% que corresponde a 24 estudiantes representan de forma correcta la función solicitada en el plano cartesiano. Además, relacionan el dominio con el eje de las X y el rango con el eje de la Y, teniendo claro el conjunto de partida y el conjunto de llegada. Solo un estudiante presentó dificultades la cual consistió en que confundió los ejes del plano cartesiano.
En el cuarto ítem se propone la articulación de registro partiendo del gráfico al algebraico y por último al enunciado, los estudiantes muestran habilidad para hallar la expresión algebraica sin hacer ningún tipo de cálculo, pero en el momento de pasarlo a un enunciado sólo algunos contestaron.
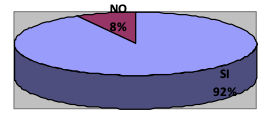
Figura 4
Representa una función en expresión
algebráica a partir de su gráfica
-----
Figura 5
Formula enunciados de funciones a
partir de una expresión algebráica
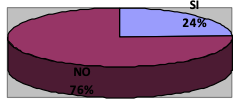
En este ítem se les pide realizar dos transformaciones, articulando en un inicio el registro gráfico al algebraico donde el 92% de los estudiantes representaron de forma correcta la expresión algebraica de la función que se les presentaba en a partir del registro gráfico. En los procesos realizados se pudo observar el uso de la ecuación de la pendiente, donde ellos seleccionaron dos puntos de la función y a partir de esto con la ecuación punto pendiente hallaban la expresión que se les solicitó. Sin embargo, aunque la mayoría de estudiantes acertaron con la expresión algebraica en el momento de generar un enunciado solo 6 formularon de manera coherente un enunciado que representara la función.
El quinto ítem se hizo uso de los conceptos de área y perímetro partiendo de un enunciado donde se debía obtener la expresión algebraica que permite dar solución a lo planteado. Los estudiantes manejan los conceptos perfectamente y llegan a la respuesta sin ningún problema.
Figura 6
Plantea una expresión algebráica
a partir de un enuciado
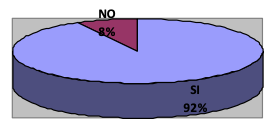
Los resultados obtenidos evidencian que un 92% de estudiantes manejan los conceptos de área y perímetro de figuras geométricas, además plantean expresiones algebraicas que les permite dar solución al problema planteado. Los 7 estudiantes que no acertaron en la solución del quinto ítem presentaban inconvenientes al desconocer las fórmulas de área de las figuras geométricas, puesto que sin este concepto no podían dar la solución correcta.
A partir de lo analizado con la aplicación de la ingeniería didáctica como metodología de investigación, que permite la aplicación de secuencias didácticas para el mejoramiento del proceso enseñanza y aprendizaje alrededor de una temática se concluyen los siguientes aspectos.
La aplicación de secuencias didácticas a los estudiantes de primer semestre permite aclarar concepciones que tienen acerca de la temática y a partir de los saberes previos empezar a fortalecer la correcta apropiación de los contenidos propios de los diversos cursos de cálculo.
Se evidenció que los estudiantes lograron avanzar en la articulación coherente de diversos registros de representación de una función, pero sigue presentándose dificultad en el registro de lenguaje cotidiano. Cabe resaltar que uno de los inconvenientes más comunes en los participantes fue la interpretación y análisis de enunciados, ya que se hace recurrente la presencia de dificultades en la comprensión y extracción de información a partir del enunciado cotidiano que les invita a procesos como el modelado matemático.
Esta investigación es un proceso de mejoramiento continuo por lo que las secuencias de intervención pedagógica se irán modificando en sus actividades con el fin de obtener mejores resultados en pruebas futuras. Uno de los cambios ya establecidos es implementar las funciones a trozos y la interpretación de enunciados en la mayoría de sesiones para dar solución a este problema que persiste en los participantes.
Artigue, M., Douady, R., Moreno, L., (1995). Ingeniería didáctica en educación matemática.
Amaya de Armas, T. Sgreccia, N. (2014) Dificultades de los estudiantes de once grado al hacer transformaciones de representaciones de una función. Épsilon - Revista de Educación Matemática. 31(3). 21-38. Recuperado de: http://thales.cica.es/epsilon/sites/thales.cica.es.epsilon/files/%5Bfield_volumen-formatted%5D/epsilon88_2.pdf
Benítez, A. (2010). Estudio numérico de la gráfica para construir su expresión algebraica. El caso de los polinomios de grado 2 y 3. Educación Matemática, 22(1), 5-29.
D’Amore, B. (2006). Objetos, significados, representaciones semióticas y sentido. Revista Latinoamericana de Investigación en Educación Matemática, 9(1), 177-195. Recuperado de https://www.clame.org.mx/relime.htm
Duval, R. (1999). Semiosis y pensamiento humano. Registros semióticos y aprendizajes intelectuales. Cali: Universidad del Valle
Duval, R. (2004). Los problemas fundamentales en el aprendizaje de las matemáticas y las formas superiores del conocimiento. Cali, Colombia. Universidad del Valle.
Duval, R. (2012). Preguntas y desafíos de la enseñanza de las matemáticas para todos: implicaciones para la investigación en didáctica. En U. Malaspina (Coord.). Resúmenes del VI Coloquio Internacional de Didáctica de las Matemáticas: avances y desafíos actuales (pp.3-6). Lima: Pontificia Universidad Católica del Perú.
Eisenberg, T. (1991). Functions and associated learning difficulties. In Advanced mathematical thinking, pp. 140-152. Springer Netherlands.
Fiallo, J. E., Parada, S. E. (2014). Curso de precálculo apoyado en el uso de geogebra para el desarrollo del pensamiento variacional. Revista Científica, 3(20). 56-71. Recuperado de: http://funes.uniandes.edu.co/11006/1/Fiallo2014Curso.pdf
Fernández, P., Vallejo, G., Livacic, P., y Tuero, E. (2014). Validez Estructurada para una investigación cuasi-experimental de calidad. Se cumplen 50 años de la presentación en sociedad de los diseños cuasi-experimentales. Anales de Psicología, 30 (2), 756-771.
Flores, C. D., Cázarez, M. D. S. V. (2004). Estabilidad y cambio de concepciones alternativas acerca del análisis de funciones en situación escolar. Epsilon: Revista de la Sociedad Andaluza de Educación Matemática" Thales", (58), 45-74.
Fabra, M., Deulofeu., J. (2000). Construcción de gráficos de funciones: “Continuidad y prototipos. RELIME. Revista latinoamericana de investigación en matemática educativa. (3). 207-230.
Guzmán., I. (1998). Registros de representación, el aprendizaje de nociones relativas a funciones: voces de estudiante. RELIME. Revista latinoamericana de investigación en matemática educativa, 1(1), 5-21.
Herrera Villamizar, N. L., Montenegro Velandia, W., & Salvador Poveda, J. (2011). Revisión teórica sobre la enseñanza y aprendizaje de las matemáticas.
Hernandez-Suarez, C. A., Prada-Núñez, R., & Ramírez-Leal, P. (2017). Obstáculos epistemológicos sobre los conceptos de límite y continuidad en cursos de cálculo diferencial en programas de ingeniería. Revista Perspectivas, 2(2), 73-83.
Hitt, F. (2003). Dificultades en el aprendizaje del cálculo. Décimo primer Encuentro de Profesores de Matemáticas del Nivel Medio Superior. Morelia. Universidad Michoacana de San Nicolás de Hidalgo.
López, J., Sosa, L. (2008). DIFICULTADES CONCEPTUALES Y PROCEDIMENTALES EN EL APRENDIZAJE DE FUNCIONES EN ESTUDIANTES DE BACHILLERATO. Acta Latinoamericana de Matemática Educativa. 21. 308-318. Recuperado de http://funes.uniandes.edu.co/4946/1/L%C3%B3pezDificultadesALME2008.pdf
Manrique, N., J., Gallo, A., M., y Prada., N. (2017). Estado del arte alrededor del concepto de función. Memorias II Encuentro Internacional en Educación Matemática.
Ministerio de Educación Nacional. (2005). Potenciar el pensamiento matemático: un reto escolar. Estándares básicos de competencias en matemáticas. Bogotá: Ministerio de Educación Nacional.
Prada, R., Hernández, C., y Ramírez, P. (2016). Comprensión de la noción de función y la articulación de los registros semióticos que la representan entre estudiantes que ingresan a un programa de Ingeniería. Revista Científica, 2(25), 188-205.
Sadovsky, P. (2005). La teoría de situaciones didácticas: un marco para pensar y actuar la enseñanza de la matemática. Reflexiones teóricas para la educación matemática.
Sánchez-Matamoros, G., García, M. y Llinares, S. (2008). La comprensión de la derivada como objeto de investigación en didáctica de la matemática. Revista Latinoamericana de Investigación en Educación Matemática, 11(2), 267-296.
Sureda, P, y Otero, M, R. (2013). Estudio sobre el proceso de conceptualización de la función exponencial. Educación matemática, 25(2), 89-118. Recuperado de http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S1665-58262013000200005&lng=es&tlng=es.
Tobón S., Pimienta J, H., y García J, A. (2010). Secuencias didácticas: aprendizaje y evaluación de competencias. México: Grupo Editorial Pearson
Vargas, M. G., Higuita, C. G., & Muñoz, D. A. J. (2015). El estado del arte: una metodología de investigación. Revista Colombiana de Ciencias Sociales, 6(2), 423-442.
Villa Ochoa, J. A., & Ruiz Vahos, H. M. (2011). Modelación en educación matemática: una mirada desde los lineamientos y estándares curriculares colombianos. Revista Virtual Universidad Católica del Norte, 1(27).
1. Cúcuta-Colombia. Universidad Francisco de Paula Santander. Licenciada en formación en Matemáticas. Miembro del Semillero en Educación Matemática adscrito al grupo de investigación GIPPED. nelcyjeriserthmj@ufps.edu.co
2. Cúcuta-Colombia. Universidad Francisco de Paula Santander. Licenciada en formación en Matemáticas. Miembro del Semillero en Educación Matemática adscrito al grupo de investigación GIPPED. ashleymiyerethgs@ufps.edu.co
3. Cúcuta-Colombia. Universidad Francisco de Paula Santander. Licenciado en Matemáticas y Computación. Magister en Educación Matemática. raulprada@ufps.edu.co