

 Vol. 40 (Nº 5) Año 2019. Pág. 17
Vol. 40 (Nº 5) Año 2019. Pág. 17
PATIÑO-CUERVO, Daniela 1; PATIÑO-CUERVO, Oliva 2; PULIDO, Óscar C. 3
Recibido: 27/09/2018 • Aprobado: 09/01/2019 • Publicado 11/02/2019
RESUMEN: El artículo propone un análisis de la práctica de una maestra novel, en perspectiva del Conocimiento Didáctico del Contenido, en los seis componentes propuestos por Park & Oliver (2008). En el primer apartado se presentan las perspectivas teóricas en relación con la didáctica general, didáctica de las Matemáticas y Conocimiento Didáctico del Contenido. En el segundo apartado se vislumbra el proceso metodológico. En el tercero y cuarto, se tratan los resultados y las conclusiones respectivamente. |
ABSTRACT: The article proposes an analysis of the practice of a novel teacher, in perspective of the Pedagogical Content Knowledge, in the six components proposed by Park & Oliver (2008). In the first section are presented the theoretical perspectives in relation to the general didactic, didactic of Mathematics and Pedagogical Content Knowledge. In the second section is exposed the methodological process. In the third and fourth section, the results and conclusions are treated respectively. |
El conocimiento Didáctico del Contenido (CDC), se sustenta y pretende que el maestro se consolide como un profesional de la enseñanza, responsable de los aprendizajes de sus estudiantes y fundamental en los procesos educacionales, y comprende una amalgama entre el conocimiento del Contenido y el conocimiento didáctico (Shulman, 2005).
En este sentido y puesto que cada maestro configurara su CDC a partir de su práctica, el docente genera conocimiento, el saber enseñado, por ejemplo, es propio del docente, es creado por él, a partir de los conocimientos que posee. La forma particular de hacer enseñable lo que sabe, es un saber didáctico particular creado por el maestro, digno de sistematizar y compartir en la comunidad científica.
Por lo anterior se plantea la pregunta ¿Cuáles son las características del Conocimiento Didáctico del contenido de una docente novel licenciada en Matemáticas, en la enseñanza del algebra?, dada la complejidad de la pregunta se realiza un análisis a partir de los seis componentes del CDC descritos por Park y Oliver (2008): finalidades de la enseñanza, evaluación, estrategias, currículo, eficacia y conocimientos de los estudiantes.
Se construyeron referentes teóricos en relación con las categorías: didáctica general, entendiendo que el CDC se instaura en una perspectiva de la didáctica como disciplina científica, Conocimiento didáctico del contenido, y Componentes del CDC del modelo de Park y Oliver (2008), apoyados en las teorías propias de la didáctica de la Matemática.
El presente texto expone algunas investigaciones realizadas en relación con Didáctica de las matemáticas desde un enfoque francés y Conocimiento Didáctico del Contenido en matemáticas, donde se resalta las conclusiones de las mismas; en la segunda parte se exponen las perspectivas teóricas de Conocimiento Didáctico del Contenido y CDC desde la perspectiva de Park y Oliver (2008); la tercera parte comprende la metodología empleada; finalmente se presentan los resultados, haciendo énfasis en las los componentes de evaluación, comprensión de los estudiantes, estrategias y sus relaciones.
En términos de Astolfi (2001), la didáctica es sustantivo más que adjetivo, es decir, no es cualidad de algo; la clase didáctica, el tablero didáctico, la mesa didáctica, son nociones equívocas de lo didáctico. Desde una perspectiva francesa, la didáctica es entendida como una Ciencia, dentro de las Ciencias de la Educación. Ciencia, puesto que posee un objeto bien definido (el aprendizaje disciplinar), conceptos fundamentales y propios producto del análisis didáctico y difiere de las demás disciplinas científicas relacionadas con la educación, pero se nutre de los conceptos y métodos que sirvan de orientación en el estudio de su objeto.
El concepto inicial de la didáctica fue el de representación mental de los objetos de conocimiento. Esta perspectiva, inicialmente, apuntaba a esclarecer las representaciones que los alumnos hacían de los conocimientos, pero, posteriormente, fue dejado de lado y en su lugar se adoptó el de concepciones de conocimiento, que está más cerca de la idea sobre un conocimiento dado, especialmente en el ámbito del conocimiento científico. (Zambrano, 2016, p. 57)
Es decir, la didáctica traslada el foco al saber, a un saber disciplinar, su objeto de estudio es “la génesis, circulación y apropiación del saber y sus condiciones de enseñanza y aprendizaje” (Zambrano, 2016, p. 57), de modo que se distinguen didácticas disciplinares, entre ellas la didáctica de las matemáticas, puesto que a cada disciplina científica como las ciencias naturales o las matemática, por definición, tiene sus propias formas de origen, circulación y apropiación de los saberes.
La didáctica de las matemáticas, y en general, la didáctica tiene su origen el estado, los docentes y teóricos franceses que determinaron una disciplina específica que se ocupa de “las cuestiones prácticas del educar y sus formas de aprendizaje” (Zambrano, 2005, p.23), en este sentido los docentes del área de las matemáticas fueron los primeros en delimitar su objeto, al preocuparse por el educar y el aprendizaje disciplinar.
Es así como para la década de los setenta se crea el Instituto de Investigación en Enseñanza de las Matemáticas (IREM), en donde se realizó una continua reflexión acerca de la formación de los docentes del área y “la investigación e innovación de la enseñanza del saber matemático” (Zambrano, 2005, p.24). Dentro de esta línea investigativa y la posterior fundación del Équipe de Recherche Mathématique a l'école Élémentaire (ERMEL), se encuentran las investigaciones de Yves Chevallard (1997), Guy Brousseau (2007) y Régine Douady (1995), que dieron origen a conceptos propios del campo científico.
En cuanto a Conocimiento Didáctico del Contenido, Pinto-Sosa (2010) afirma que el CDC del docente de matemáticas depende de la noción de la ciencia, la condiciones de su formación profesional, y su propia experiencia, para el caso específico de la estadística, los docentes cuya formación profesional difiere de la matemática, suelen tener una noción instrumentalista de la misma, es decir, la conciben como un repertorio de algoritmos o fórmulas; por tanto, la enseñanza está centrada en demostraciones y reglas de procedimientos.
Por su parte Hauk, Toney, Jackson, Nair, y Tsay (2014) incorporan la comunicación en la matemática como parte del conocimiento de las estrategias y lo denominan Conocimiento del discurso, teniendo como supuesto que la eficacia en la enseñanza de la matemática no depende únicamente de lo que es dicho, sino de cómo y quién lo dice, y con qué garantía. El maestro debe entonces, conocer las experiencias e intereses de sus estudiantes, no sólo en el área de las matemáticas, sino de su vida misma.
De otro lado, Solar y Rojas (2015) aseguran que la relación entre el conocimiento del contenido, el conocimiento de los estudiantes y las estrategias, es el fundamento para la planificación de las clases. Las estrategias configuradas se basan y deben responder a las evidencias de los aprendizajes.
En cuanto al CDC en la enseñanza del álgebra, Ladele, Ormond, y Hackling (2014) realizaron una investigación en el contexto Nigeriano, en la cual enfatizan en la experiencia como fundamento del CDC, dado que encuentran que los maestros noveles suelen tener dificultades en la enseñanza del álgebra, al punto de replicar errores en los conceptos de variable y ecuación, por ejemplo, la letra algebraica es entendida como una palabra u objeto y no como una cantidad. Además aseguran que el álgebra es la introducción a las matemáticas superiores; por tanto, su instrucción debe ser eficaz, de lo contrario los estudiantes encontrarán dificultades en los grados avanzados.
Desde las investigaciones estadounidenses se incorporan al campo Didáctico, entre otros conceptos, el Conocimiento Base, Conocimiento de la Materia, Conocimiento Didáctico y el Conocimiento Didáctico del Contenido, a partir de las investigaciones de Lee S. Shulman (2005), Pamela L. Grossman (2005), Soonhye Park y J. Steve Oliver (2008), por ejemplo.
La noción de conocimiento base, surge de la intención de los educadores estadounidenses, de instaurar el ejercicio de la enseñanza como una profesión, con el fin de hacer de la docencia una ocupación “más respetada, más responsable, más gratificante y mejor remunerada” (Shulman, 2005, p. 4). La profesionalización de la enseñanza tiene por supuesto, la posibilidad de sistematizar y mejorar los parámetros con los cuales se evalúa el desempeño de los profesionales de la educación, lo cual implica la existencia de un “conocimiento base para la enseñanza”, esto es un “conjunto codificado o codificable de conocimientos, destrezas, comprensión y tecnología, de ética y disposición, de responsabilidad colectiva” (Shulman, 2005, p.4) necesarios para una enseñanza eficiente.
Para Shulman (2005), la enseñanza se define especialmente a partir del maestro, sin ubicarse en el extremo de menospreciar la importancia del estudiante en este proceso. La enseñanza tiene como fin lograr que los estudiantes “aprendan a comprender y a resolver problemas, que aprendan a pensar crítica y creativamente y que aprendan datos, principios y normas de procedimiento.” (Shulman, 2005, p. 9). Así que, por un lado, se traspasa del sentido de la enseñanza como simple transmisión de contenidos a entes pasivos y de otro lado, se entiende que aun cuando el aprendizaje es responsabilidad del estudiante, el maestro, como profesional de la enseñanza, es responsable de crear los dispositivos didácticos necesarios para configurar condiciones propicias para el aprender.
Shulman (2005) propone entonces siete categorías del conocimiento base para la enseñanza: el conocimiento del contenido, de la didáctica general, del currículo, de los alumnos, de los contextos educativos, de los objetivos, las finalidades y los valores educativos, y sus fundamentos filosóficos e históricos y el Conocimiento Didáctico del Contenido (CDC).
El Conocimiento Didáctico del Contenido es una mezcla especial entre Conocimiento de la Materia o del Contenido (CM) y Conocimiento Didáctico. Lo cual implica que ser experto en un saber no es garantía para ser un profesional de la enseñanza, por ejemplo, el matemático, quién comprende y produce saberes en esta disciplina, dista del docente de matemáticas, puesto que carece de saberes didácticos.
No se entiende, entonces, que el experto esté imposibilitado para llegar a ser un profesional docente, es decir, no está exento del estudio e investigación de la didáctica, del currículo y de los contextos y fines educativos.
El conocimiento Didáctico, componente del CDC, hace referencia al conocimiento de las teorías didácticas, generales o disciplinares, que se materializan en el contexto específico de una clase. El conocimiento del contenido, por su parte, se refiere a:
… la "materia" de una disciplina: información objetiva, organización de principios, conceptos centrales (…) Además de la habilidad para identificar, definir y discutir estos conceptos separadamente, un individuo con conocimiento del contenido puede identificar relaciones entre conceptos en un campo al igual que relaciones con conceptos externos a la disciplina. (Grossman, Wilson, & Shulman, 2005, p.11).
El CM comprende dos dimensiones: la sustantiva que abarca las teorías que soportan la disciplina científica; la sintáctica, que hace referencia a la forma particular de génesis de saberes de dicha disciplina (Grossman et al., 2005).
Modelo de Park y Oliver (2008). Estos investigadores evalúan, a partir de la investigación empírica, la construcción del CDC, tomando como referente el modelo pentagonal de componentes presente en los estudios de Grossman (1990), Tamir (1988) y Magnusson, Krajcik y Borko (1999), en este modelo se incluye los conocimientos sobre: finalidades de la enseñanza científica, estrategias, currículo, evaluación y comprensión de los estudiantes que se refiere al conocimiento del grado de aprendizaje de cada uno (Park & Oliver, 2008).
De igual manera, en la investigación emerge una categoría denominada “eficacia” y determina las creencias de los docentes sobre su capacidad para emplear estrategias de enseñanza, es decir, la percepción que tiene el docente de sí mismo acerca de su capacidad para hacer enseñable lo que sabe, además de la experticia en el objeto de enseñanza.
Las orientaciones de la enseñanza o finalidades, se relacionan con la perspectiva epistemológica que tiene el docente en relación con un saber, que permean lo que considera o cree que son los objetivos de la enseñanza de la ciencia, es la construcción propia de respuestas a los cuestionamientos de ¿por qué enseñar matemáticas? y ¿para qué enseñarla?
En el caso de las matemáticas, ciertas escuelas de pensamiento han aportado una noción propia de lo que es las matemáticas, para el Platonismo e Idealismo los objetos matemáticos no son objetos físicos, aunque reales, hacen parte del mundo de las ideas “donde se encuentran las verdades absolutas, inmutables, seguras e indestructibles” (Espinosa, 2010).
Para el Logicismo, la matemática es una estructura lógica, carente de contradicciones, en este sentido, la enseñanza tiene como fin evidenciar las estructuras de las matemáticas. El formalismo, por su parte, indica que las matemáticas son un juego simbólico, y enseñarla consiste en “evidenciar los aspectos sintácticos de combinación de los signos formales” (Fandiño, 2006, p.47)
De otro lado, la matemática bajo la perspectiva social, en la cual la matemática “constituye una actividad humana, simultáneamente individual y social, que es producto del diálogo entre quienes intentan resolver un problema” (Espinosa, 2010, p.147) con un enfoque casi-empírico, que implica que las estrategias de enseñanza se fundamenten en la resolución de problemas análogos a los procesos que llevaron a la génesis de los saberes que se pretenden enseñar.
Son organizadas en: de la materia, las cuales hacen referencia a las estrategias de enseñanza generales que se articulan con los objetivos de la enseñanza del maestro; y para temas específicos, que aluden a las estrategias de instrucción propias de un objeto de enseñanza de una ciencia específica (Park & Oliver, 2008).
En el campo de la didáctica de las matemáticas, las estrategias de enseñanza generales se articulan a partir de conceptos teóricos propios, por ejemplo, la transposición didáctica, ingeniería didáctica, situaciones didácticas y el enfoque socioepistemológico.
Según Chevallard (1997), en los años noventa, dentro del sistema didáctico, se dio, de manera equívoca, demasiada importancia a la relación maestro – estudiante y se olvidó la pregunta por el saber. Sin embargo, la posibilidad de cuestionar ese tercer vértice del triángulo didáctico implica plantear las preguntas que orientan el objeto de estudio de la didáctica de las matemáticas.
… ¿qué es entonces aquello que, en el sistema didáctico, se coloca bajo el estandarte del Saber? El “saber enseñado” que concretamente encuentra el observador, ¿qué relación entabla con lo que se proclama de él fuera de ese ámbito? ¿Y qué relación entabla entonces con el “saber sabio”, el de los matemáticos? ¿Qué distancias existen entre unos y otros? (Chevallard, 1997, p. 4).
La transposición didáctica es entonces una forma de respuesta a estos cuestionamientos y hace referencia al paso del saber sabio al saber enseñado, en este sentido supone por definición una distancia entre los dos saberes, el saber sabio generado por los matemáticos para dicha disciplina, a través de procesos de investigación, y el saber enseñado (saber escolar), el que se lleva a las aulas (Chevallard, 1997).
Durante el proceso de transposición se encuentra un saber intermedio, que hace referencia al saber curricularizado, el saber para enseñar, o saber objeto de enseñanza, el cual hace referencia a los contenidos que los estamentos estatales y las instituciones educativas, según su autonomía, establecen como imprescindibles y necesarias para determinado contexto y nivel escolar, siguiendo los ideales educativos de la época.
El saber enseñado, por su parte, hace referencia al saber propio del docente, producto del proceso de trasposición, en el cual se entretejen saberes disciplinares, saberes relacionados con las prácticas, posturas epistemológicas y con lo cual busca hacer comprensible el saber que posee, es decir “lo que realmente se enseña no es el saber puro de la ciencia, sino el saber disgregado entre poder, actitud y práctica” (Zambrano, 2005, p.50).
De otro lado, en 1989 se lleva a cabo la Quinta Escuela de Verano de Didáctica de las Matemáticas en Plestin les Grèves, Francia, en la cual Michèle Artigue, presenta un curso relacionado con un nuevo concepto, la Ingeniería Didáctica, investigado de igual forma por Guy Brousseau y Régine Douady (Artigue, 1995). La ingeniería didáctica tiene su origen en los inicios de los años ochenta y hace referencia a un modo de ejercicio didáctico análogo al trabajo del ingeniero, es decir, el trabajo didáctico comprende la invención y utilización de conocimientos científicos del campo disciplinar didacta para la realización de un proyecto de aprendizaje para determinado objeto de saber y grupo de estudiantes (Artigue, 1995; Douady, 1995). La ingeniería didáctica también se refiere a un tipo de metodología de investigación de tipo experimental que utiliza los estudios de caso con validación interna. Su validez no depende de una comparación cuantitativa; además, estudia las secuencias de enseñanza a partir de su realización, observación y análisis (Artigue, 1995).
Por su parte, Guy Brousseau cuestiona y analiza las prácticas de los docentes de matemáticas, en las cuales el estudiante es un espectador de ejemplos y aplicaciones o lecturas simples de enunciados, teoremas o definiciones matemáticas, que si bien pueden, en algunos casos, ser sugestivas y lograr que el estudiante produzca algún tipo de conocimiento, no son los suficientemente motivantes (Brousseau, 2000), es decir, “si el desarrollo de los conocimientos y de las competencias es una adaptación, es necesario crear ocasiones para que el alumno se sienta motivado para adaptarse a nuevas situaciones” (Zambrano, 2005, p.57). En este sentido, Brousseau (2007) propone la teoría de las Situaciones Didácticas. Una situación es “un modelo de interacción entre un sujeto y un medio determinado” por lo que una situación didáctica hace referencia a la disposición, planeada o no por el maestro, de un conjunto de elementos que intervienen en el aprendizaje de determinado saber objeto de enseñanza. En las situaciones didácticas el docente declara explícitamente los objetivos de la clase, los saberes que se quieren alcanzar y se requiere que las condiciones de un contrato didáctico para lograr dichos objetivos, por tanto se proponen las Situaciones a-didácticas, en las cuales el estudiante desconoce los objetivos de aprendizaje que determina el docente, “el estudiante afronta una actividad que lo involucra, pero no sabe si tiene o no una finalidad cognitiva” (Fandiño, 2006, p.64).
Por su parte, Cantoral (2004) expone el enfoque socioepistemológico, descrito por primera vez en 1997 en México:
La socioepistemología, o epistemología de las prácticas sociales relativas al saber, es una aproximación teórica de naturaleza sistémica que permite tratar con los fenómenos de producción y difusión del saber desde una perspectiva múltiple, pues articula en una misma unidad de análisis a las interacciones entre la epistemología del conocimiento, su dimensión sociocultural, los procesos cognitivos que le son asociados y los mecanismos de su institucionalización vía la enseñanza (Cantoral, 2004, p.1).
El enfoque sociepistemico, entonces, “defiende la idea de que el conocimiento se construye a partir de las prácticas sociales.” (Espinosa Romero & Jiménez Espinosa, 2014). Desde este enfoque, el docente se cuestiona acerca de cuáles son las prácticas sociales que permiten a los estudiantes percibir y determinar un saber objeto de enseñanza, de manera que la respuesta a esta pregunta direccione la creación de dispositivos o estrategias didácticas.
De igual manera el componente currículo comprende dos elementos, el primero se refiere a la coherencia o relación de los contenidos de la asignatura con los contenidos de las demás áreas en un grado escolar, esto es, currículo horizontal. El segundo encierra la concordancia de los objetos de enseñanza de una ciencia en un grado escolar, con los ya impartidos en años anteriores y los que se tendrán en cuenta en los años siguientes, a este elemento se le denomina currículo vertical.
En el contexto Colombiano el Ministerio de Educación Nacional (MEN) propone los estándares básicos de competencias en matemáticas. Un estándar es una situación deseada, en relación con los aprendizajes de un área y grado escolar especifico y sirve como medida para juzgar si el estudiante y la institución educativa cumple con las condiciones de calidad que persigue el modelo educacional colombiano (Ministerio de Educación Nacional de Colombia, 2014).
Los estándares están distribuidos por secciones de grados escolares, primero a tercero, cuarto a quinto, sexto a séptimo, octavo a noveno y décimo a undécimo; y por pensamientos: Numérico y sistemas numérico, espacial y sistemas geométricos, Métrico y sistemas de medidas, aleatorio y sistemas de datos, variacional y sistemas algebraicos y analíticos (Ministerio de Educación Nacional de Colombia, s. f.).
Sobre estos estándares cada institución diseña su plan de área en el cual se contempla una malla curricular con los contenidos, saberes objeto de enseñanza para cada grado escolar. Para el grado octavo, por ejemplo, se contemplan como temas generales como, conjuntos numéricos, expresiones algebraicas, productos notables y cocientes notables y factorización, en relación con los estándares “Construyo expresiones algebraicas equivalentes a una expresión algebraica dada” y “Uso procesos inductivos y lenguaje algebraico para formular y poner a prueba conjeturas”.
De otro lado, Fandiño (2006) propone algunas tendencias deseables del currículo en matemáticas, cuyo objetivo es “la construcción del propio conocimiento, tratando una matemática accesible a todos e interesante para cada uno” en relación con la enseñanza, aprendizaje y evaluación. En la enseñanza se incluye trabajo en grupo, motivación, uso de situaciones a-didácticas, modelización de fenómenos sociales y naturales y conexión con el mundo cotidiano; en el aprendizaje, fomentar la comprensión duradera, descubrimiento e investigación, y llevar un ritmo personalizado; en la evaluación, dejar a un lado la evaluación por algoritmos, cuantitativa y de ignorancias o falta de aprendizajes.
Está compuesta por los métodos de evaluación propios de la ciencia, y los ritmos y estilos de aprendizaje.
En los estándares básicos de competencias en matemáticas se establece una evaluación de tipo formativo en la cual se realiza una valoración constante, fundada en la observación atenta y paciente, en relación con la manera como los estudiantes, interpretan, formulan y solucionan un problema matemático (Ministerio de Educación Nacional de Colombia, s. f.).
Por su parte, Fandiño (2006) propone las siguientes dimensiones de la evaluación en matemáticas, como respuesta a la pregunta ¿Por qué se evalúa y qué se evalúa?:
- Se evalúa para tomar decisiones acerca del contenido (trasposición didáctica) y acerca de la metodología de trabajo en el aula (ingeniería didáctica).
- Se evalúa para tomar decisiones acerca del ambiente del aula
- Se evalúa para comunicar a los estudiantes aquello que es importante
- Se evalúa para dar una “nota” (pp. 88-89)
La investigación se desarrolló con un enfoque interpretativo derivado de la naturaleza misma del estudio, en el que se pretende interpretar una práctica docente apoyada en los seis componentes del Conocimiento Didáctico del Contenido propuestas por Park y Oliver (2008). El término interpretativo implica “todo el conjunto de enfoques de la investigación observacional participativa. (…) El interés de la investigación se centra en el significado humano en la vida social y en su dilucidación y exposición por parte del investigador” (Erickson, 1986, p.196).
El contexto de estudio comprende la práctica docente de una maestra novel, licenciada en Matemáticas, con dos años de experiencia. El proceso se analizó específicamente en el Grado Octavo de una institución educativa pública de Boyacá, Colombia.
La investigación se constituyó en tres fases: la primera consistió en una revisión teórica de las categorías principales: didáctica, didáctica de las matemáticas y Conocimiento Didáctico del Contenido; la segunda comprende la recolección de datos, para lo cual se utilizó la observación no participante de una clase de matemáticas, para conocer y comprender el objeto de investigación, tal como se presenta (Angulo-Rasco & Catalán, 2017), y la entrevista semiestructurada en la que se planificaron los ámbitos sobre los cuales indagar y se diseñó un cuestionario propenso a modificaciones en el proceso (Vallejos & Angulo - Rasco, 2017).
Finalmente, se realizó un análisis del contenido, que “[consiste] en explicitar y sistematizar el contenido de los mensajes y la expresión de ese contenido con la ayuda de indicios cuantificables o no” (López, 2002, p. 175), por medio del software de análisis de datos cualitativos ATLAS.ti versión 8.0 en el cual se realizaron los procesos de comparación, contrastación y agregación, de las entrevistas y la transcripción de la clase observada. Esto permitió visualizar enraizamiento (citas asociadas a la categoría) y densidad (relaciones de una categoría o subcategoría con otras subcategorías) para finalmente construir significados.
Como resultado del análisis de los datos en el Software Atlas Ti versión 8.0, se encuentra un mayor enraizamiento (E) y densidad (D) en las categorías Estrategias y Compresión de los estudiantes (Figura 1), lo cual implica que el CDC en relación a la enseñanza del álgebra, de la docente sujeto de estudio, se fundamenta en estos dos componentes.
Figura 1
CDC de la Docente a partir del análisis en ATLAS.ti
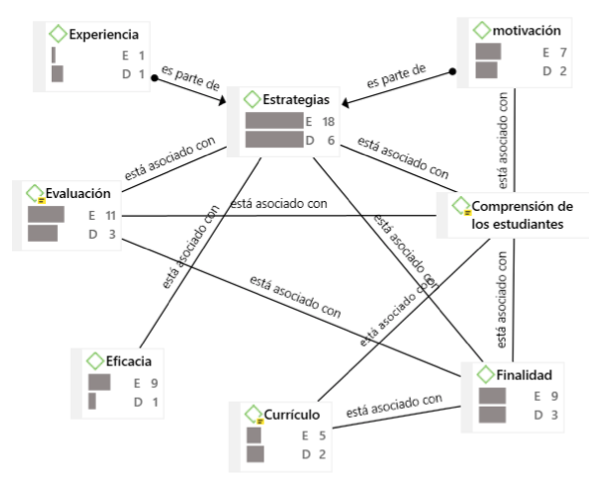
(Fuente: elaboración propia).
La comprensión de los estudiantes y la evaluación tienen una relación bidireccional, se evalúa la comprensión y sobre esta, es decir, en la evaluación constante de tipo diagnostica realizada por la maestra, se busca entender en qué medida el estudiante ha apropiado el saber objeto de enseñanza, y sobre el nivel medio de comprensión se realizan las evaluaciones sumativas. Además, la docente evalúa para tomar decisiones sobre las estrategias que debe utilizar, pues si bien ella aplica evaluaciones en cumplimiento de los estatutos de la institución educativa, es decir para dar una nota, también evalúa constantemente de forma oral, por medio de cuestionamientos y actividades que no necesariamente se verán representadas en una calificación.
Entonces uno no solo le hace las evaluaciones escritas sino orales y en todo momento, que pasen al tablero y desarrollen algo, que digan qué significa un concepto, en las tareas, hay muchas maneras de darse cuenta de que ellos saben. (Información Verbal en Entrevista I. [14 de mayo de 2018] Entrevistadora: Daniela Patiño Cuervo. Tunja)
Es decir, a partir de las observaciones en el aula a propósito del desarrollo de los trabajos, y del análisis de los trabajos escritos u orales “se pueden identificar puntos fuertes y puntos débiles de cada estudiante (…) y de esa manera decidir consecuentemente por las elecciones relativas a la transposición didáctica y por una determinada ingeniería didáctica” (Fandiño, 2006, p.88).
A partir de la evaluación de las actitudes de su grupo de estudiantes, la docente adquiere el conocimiento sobre el bajo nivel de motivación de sus estudiantes, e intenta encaminar sus estrategias hacía la motivación, para lo cual adopta como directriz la Matemática Recreativa, con el objetivo de captar el interés del estudiante por medio de un truco o un chiste de manera que se vaya conduciendo a los saberes, sin que este note lo que está sucediendo (Torres & Zuluaga, 2008).
Cómo lo afirma la docente:
…me he dado a la tarea de buscar estrategias para que ellos se motiven, porque a ellos les parece muy aburrido el tema del álgebra, la tarea es buscar actividades con las cuales se pueda trabajar ese tema y llevarlas y hacer la clase más amena. (Información Verbal en Entrevista I. [14 de mayo de 2018] Entrevistadora: Daniela Patiño Cuervo. Tunja)
La motivación es entonces la base sobre la cual articula sus estrategias, entendiendo que la actitud de los estudiantes frente a un saber condiciona el aprendizaje del mismo.
La experiencia de la docente y el análisis de su práctica es fundamento de su CDC, puesto que, si bien cuenta con aproximadamente dos años de experiencia, el continuo análisis de sus clases le ha permitido consolidar su propio saber profesional, pues algunas estrategias utilizadas, que en la teoría parecen ser infalibles, en la práctica resultan confusas para el estudiante y crean en él vicios que lo alejan del aprender. En su primer acercamiento con la enseñanza del algebra intentó incorporar el álgebra geométrica como estrategia didáctica, en la cual se hace uso de áreas, perímetros, volúmenes que pueden representar y ser la introducción a algunos casos de factorización, como el trinomio cuadrado perfecto; Ballen (2012), en su tesis de maestría, afirma que:
La introducción al álgebra a través de la geometría es una herramienta y a la vez una alternativa didáctica que logra en un primer momento fortalecer el paso del lenguaje natural al lenguaje algebraico. Permite dar significado al concepto de variable, a las expresiones algebraicas y a las operaciones básicas, para posteriormente introducir la noción de factorización (p. 4).
Sin embargo, con esta actividad, más que permitir el desarrollo del pensamiento algebraico, simplemente logró un cambio en el objeto de repetición más que la reproducción no racionalizada de conceptos, pues ya no acudían a la igualdad algebraica de ![]() para duplicarla en los ejercicios, sino al cubo tridimensional de 3×3, sin el cual les era imposible el desarrollo de algún problema de factorización.
para duplicarla en los ejercicios, sino al cubo tridimensional de 3×3, sin el cual les era imposible el desarrollo de algún problema de factorización.
Esta ruptura entre teoría y práctica puede generar desmotivación en el maestro que intenta innovar en sus estrategias, como la docente asegura: “a veces uno quisiera dejar de ser tradicional, pero no funciona, lo que funciona es lo tradicional, entonces pienso, ¿será que perdí el tiempo poniéndoles esa actividad?” (Información Verbal en Entrevista I. [14 de mayo de 2018] Entrevistadora: Daniela Patiño Cuervo. Tunja).
De otro lado, la perspectiva epistemológica que ha construido la docente tiene cierta relación con el enfoque socioepistémico de las matemáticas,
Las matemáticas son una manera de comprender los fenómenos o eventos del contexto, del mundo, de la vida, son útiles en la vida, existen temas básicos que son aplicables al quehacer diario y facilitan muchas cosas, y otros más profundos que se utilizan en carreras o en oficios más específicos. (Información Verbal en Entrevista I. [14 de mayo de 2018] Entrevistadora: Daniela Patiño Cuervo. Tunja).
Sin embargo, si bien en el discurso la maestra no “desconoce las aplicaciones de la teoría matemática y de los conceptos tal como ellos se presentan en el mundo físico” (Espinosa, 2010, p. 145) e identifica la parte representacional y social de las matemáticas, sus práctica responden a una perspectiva formalista donde los ejercicios y “problemas” son repetitivos y se resuelven aplicando reglas (Fandiño, 2006). Las actividades de motivación no ofrecen la oportunidad al estudiante de un descubrimiento personal de los saberes objeto de enseñanza; funcionan en su lugar como actividades de ejercitación o de evaluación, puesto que su desarrollo implica la aplicación de reglas previamente impartidas como algo rígido y acabado.
Finalmente, la maestra considera que, el álgebra es el punto de acceso a constructos matemáticos avanzados y su ubicación en la malla curricular responde a esta premisa, no obstante, en la práctica, se encuentra que en el grado Octavo los estudiantes al no haber logrado el aprendizaje de algunos conceptos básicos de las matemáticas, la enseñanza del álgebra se torna en un refuerzo de los contenidos de grados anteriores.
Me queda la satisfacción de que hagan las operaciones de los números enteros bien, y que entiendan las propiedades de las operaciones de los números enteros, la potenciación y demás, porque, por ejemplo, en grado once no se les puede poner a desarrollar una ecuación cuadrática, porque se les dificulta despejar una ecuación lineal, entonces, que los de grado octavo realicen bien operaciones con enteros, es algo bueno. (Información Verbal en Entrevista I. [14 de mayo de 2018] Entrevistadora: Daniela Patiño Cuervo. Tunja).
Si bien, el currículo responde a la finalidad de la enseñanza de un tema particular, y la distribución de las temáticas por niveles se organiza según una coherencia horizontal, es decir, que los contenidos que se abordan en una sesión de clase, están estrictamente relacionados y son el requisito para las sesiones posteriores. De manera que, si hay una ruptura en el aprendizaje de un concepto, inmediatamente la relación currículo-finalidad se disuelve. Entonces el maestro tiene la opción de continuar con las directrices del currículo e ignorar el bajo nivel de comprensión de sus estudiantes, o ignorar el mismo currículo y propender porque sus estudiantes, o al menos la mayoría alcances los aprendizajes mínimos para continuar.
El conocimiento didáctico del contenido de la docente se configura a partir de la comprensión de los estudiantes y las estrategias encaminadas a la motivación, de modo que por medio de la evaluación constante del rendimiento y de la actitud de sus estudiantes, construye sus estrategias didácticas.
Si bien la noción que se tiene de las matemáticas determina lo que el docente quiere desarrollar en sus estudiantes, se encuentra que en la práctica las estrategias no responden a las finalidades previstas, aun cuando la docente concuerda con el enfoque socioepistémico de las matemáticas, sus estrategias son de tipo formalista.
Las condiciones del contrato didáctico para la clase de matemáticas pueden llegar a estar tan arraigadas en el estudiante, que, aun cuando se cambie la metodología e incluso el mismo maestro, los estudiantes siguen los mismos acuerdos. Las nociones de matemáticas que hayan construido en la básica primaria difícilmente se modifican en la básica secundaria o en el nivel universitario.
Angulo Rasco, J. F., & Catalán, J. (2017). Observar no es lo mismo que ver. La observación etnográfica. En S. Rendon Pantoja & J. F. Angulo Rasco, Investigación Cualitativa en Educación (pp. 83–94). Buenos Aires: Miño y Dávila editores.
Artigue, M. (1995). Ingenieria Didáctica. En M. Artigue, R. Douady, & L. Moreno, P. Gómez (Ed.), Ingeniería didáctica en educación matemática (pp. 33–60). Bogotá: Grupo Editorial Iberoamérica. Recuperado a partir de http://funes.uniandes.edu.co/676/
Astolfi, J. (2001). Didáctica. En J. Astolfi, Conceptos clave en la didáctica de las disciplinas (pp. 73–82). Sevilla. España: Diada Editora.
Ballén, J. (2012). El álgebra geométrica como recurso didáctico para la factorización de polinomios de segundo grado (Tesis de Maestría). Universidad Nacional de Colombia, Bogotá.
Brousseau, G. (2000). Educación y didáctica de las matemáticas. Educación Matemática, 12(1), 5–38.
Brousseau, G. (2007). Iniciación al estudio de la teoría de las situaciones didácticas/ Introduction to study the theory of didactic situations: Didactico/ Didactic to Algebra Study. Buenos aires: Libros del Zorzal.
Cantoral, R. (2004). Desarrollo del pensamiento y lenguaje variacional, una mirada socioepistemológica. En L. Díaz (Ed.), Acta Latinoamericana de Matemática Educativa (Vol. 17, pp. 1–9). México, DF: Comité Latinoamericano de Matemática Educativa A. C. Recuperado a partir de http://funes.uniandes.edu.co/6235/
Chevallard, Y. (1997). La transposición didáctica. Buenos aires: Aique, grupo editor.
Douady, R. (1995). La ingeniería didáctica y la evolución de su relación con el conocimiento. En M. Artigue, R. Douady, & L. Moreno, P. Gómez (Ed.), Ingeniería didáctica en educación matemática (pp. 61–96). Bogotá: Grupo Editorial Iberoamérica. Recuperado a partir de http://funes.uniandes.edu.co/676/
Erickson, F. (1986). Métodos cualitativos de investigacion sobre la enseñanza. En M. Wittrock, La Investigación en la Enseñanza, II. Métodos cualitativos y de Observación (pp. 195–301). Barcelona: Paidós.
Espinosa, A. J. (2010). La naturaleza de la Matemática, sus concepciones y su influencia en el salón de clase. Educación Y Ciencia, (13). Recuperado a partir de https://revistas.uptc.edu.co/index.php/educacion_y_ciencia/article/view/765
Espinosa Romero, C. I., & Jiménez Espinosa, A. (2014). Construcción del concepto de razón y razón constante desde la óptica socioepistemológica. Praxis & Saber, 5(9), 53–80. https://doi.org/10.19053/22160159.2993
Fandiño, M. (2006). Curriculo, Evaluación y Formación docente en matemáticas. Bogotá: Magisterio editorial.
Grossman, P. L. (1990). The making of a teacher: Teacher knowledge and teacher education. Columbia: Teachers College Press.
Grossman, P. L., Wilson, S. M., & Shulman, L. S. (2005). Profesores de sustancia: El conocimiento de la materia para la enseñanza. Profesorado. Revista de currículum y formación del profesorado, 9(2), 1–25.
Hauk, S., Toney, A., Jackson, B., Nair, R., & Tsay, J.-J. (2014). Developing a Model of Pedagogical Content Knowledge for Secondary and Post-Secondary Mathematics Instruction. Dialogic Pedagogy, 2. Recuperado a partir de https://eric.ed.gov/?q=pck+algebra&id=EJ1148845
Ladele, O., Ormond, C., & Hackling, M. (2014). The Effect of Professional Learning on Early Algebra Teachers’ Content Knowledge in Nigeria. En Annual Meeting of the Mathematics Education Research Group of Australasia (Vol. 37). Sydney: Mathematics Education Research Group of Australasia. Recuperado a partir de https://eric.ed.gov/?id=ED572607
López, F. (2002). El análisis de contenido como método de investigación. Revista de Educación, (4), 167–179.
Magnusson, S., Krajcik, J., & Borko, H. (1999). Nature, Sources, and Development of Pedagogical Content Knowledge for Science Teaching. En J. Gess-Newsome & N. G. Lederman (Eds.), Examining Pedagogical Content Knowledge: The Construct and its Implications for Science Education (pp. 95–132). Dordrecht: Springer Netherlands. https://doi.org/10.1007/0-306-47217-1_4
Ministerio de Educación Nacional de Colombia. (2014). Estándares Básicos de competencia. Recuperado 6 de junio de 2018, a partir de https://www.mineducacion.gov.co/1759/w3-article-340021.html
Ministerio de Educación Nacional de Colombia. (s. f.). Estándares básicos de Competencia en Matemáticas. Recuperado a partir de https://www.mineducacion.gov.co/1621/articles-116042_archivo_pdf2.pdf
Park, S., & Oliver, J. S. (2008). Revisiting the Conceptualisation of Pedagogical Content Knowledge (PCK): PCK as a Conceptual Tool to Understand Teachers as Professionals. Research in Science Education, (38), 261–284. https://doi.org/DOI 10.1007/s11165-007-9049-6
Pinto Sosa, J. E. (2010). Conocimiento Didáctico Del Contenido Sobre La Representación De Datos Estadísticos: Estudios De Casos Con Profesores De Estadística En Carreras De Psicología Y Educación (Tesis doctoral). Universidad de Salamanca, Salamanca.
Shulman, L. S. (2005). Conocimiento y enseñanza: fundamentos de la nueva reforma. Revista de currículum y formación del profesorado, 9(2), 1–29.
Solar, H., & Rojas, F. (2015). Elaboración de orientaciones didácticas desde la reflexión docente: el caso del enfoque funcional del álgebra escolar. Revista Electrónica de Investigación en Educación en Ciencias, 10(1), 14–34.
Tamir, P. (1988). Subject matter and related pedagogical knowledge in teacher education. Teaching and Teacher Education, 4(2), 99–110. https://doi.org/10.1016/0742-051X(88)90011-X
Torres, G., & Zuluaga, C. (1998). Matemática Recreativa: Temáticas y Aspectos Didáctocos para la Educación Básica. Bogotá: Editorial Universidad inca de Colombia.
Vallejos, N., & Angulo Rasco, J. F. (2017). La entrevista etnográfica. En S. Rendon Pantoja & J. F. Angulo Rasco, Investigación Cualitativa en Educación (pp. 105–116). Buenos Aires: Miño y Dávila editores.
Zambrano, A. (2005). Didática, Pedagogía y Saber. Bogotá: Editorial Magisterio.
Zambrano, A. (2016). Pedagogía y didáctica: esbozo de las diferencias, tensiones y relaciones de dos campos. Praxis & Saber, 7(13), 45–61. https://doi.org/10.19053/22160159.4159.
1. Universidad Pedagógica y Tecnológica de Colombia. Licenciada en Matemáticas. daniela.patino@uptc.edu.co
2. Universidad Pedagógica y Tecnológica de Colombia. Magister en Educación. oliva.patino@uptc.edu.co
3. Universidad Pedagógica y Tecnológica de Colombia. Doctor en Ciencias de la Educación. oscar.pulido@uptc.edu.co