

Vol. 40 (Nº 3) Año 2019. Pág. 12
SOCORRO, Félix O. 1; REYES, Giovanni E 2.; TRUJILLO, Rodrigo A. 3
Recibido: 16/08/2018 • Aprobado: 14/12/2018 • Publicado 28/01/2019
3. Escenarios para la toma de decisiones
RESUMEN: Los escenarios utilizados en la planificación estratégica pueden ser ampliados y/o complementados si se incorporan de los escenarios irreales no utópicos aquí propuestos. Estos escenarios aportarían una visión no convencional que superaría los límites del análisis tradicional y exigiría a los decisores plantearse respuestas, consecuencias o soluciones alternativas. Los escenarios aquí planteados representan una propuesta ajustada a un mundo cambiante que exige flexibilidad y amplitud en la toma de decisiones, así como en otros campos donde puedan aplicarse. |
ABSTRACT: The scenarios used in strategic planning can be expanded and / or supplemented through the incorporation of the non-utopian unreal scenarios. These scenarios would provide an unconventional vision that would surpass the limits of traditional analysis and help to decision-makers to consider answers or solutions that, without then, were not considered Non-utopian unreal scenarios represent a proposal adjusted to a changing world that demands breadth in decision-making, as well as in other fields where they can be applied. |
Para Fred R. David (2003), citado por Conill, Hernández, & Chumaceiro (2011), los escenarios se pueden describir como “conjuntos alternativos de posibles ocurrencias futuras donde se anticipa el impacto de diversos argumentos en una organización, erigiéndose esta probablemente como la técnica más popular de la predicción social” (p.279).
Sin embargo, según Conill, Hernández, & Chumaceiro (2011), el método de escenarios comenzó a ser utilizado a mediados de los años cincuenta, dentro de los estudios estratégicos y militares desarrollados por la Rand Corporación, por lo que puede intuirse que estudiar escenarios no es exclusivo de estudios sociales, ya que éstos se revisan, se plantean y se construyen al momento de idear una estrategia, ya sea financiera, de mercadeo, política o económicas, además de las militares y, más aún, si lo que surge de ese escenario conllevará a la toma de decisiones en cualquier campo.
Al revisar la literatura asociada al tema resulta que, al parecer, son tres los escenarios más populares al estudiar las consecuencias de cualquier acción, al planear una estrategia o buscar la elección más óptima cuándo se desea tomar una decisión.
Estos escenarios suelen ser el optimista, el pesimista y el tendencial, a éste último se le conoce también por otros nombres como lo son real, conservador o normal.
Cada escenario posee ciertas características relacionadas con los límites del problema planteado y están ajustados, como se verá más adelante, a lo que se espera encontrar de darse alguno de ellos.
Ahora bien, al pensar en esos tres escenarios, desde una perspectiva crítica, es posible preguntarse: ¿son esos tres los escenarios, planteados por varios autores, suficientes para tomar la decisión o plantear la estrategia?
A juicio de los autores, tanto los tres escenarios nombrados anteriormente como otros, que se estudiarán en las páginas siguientes, no son suficientes para lograr abarcar todas las posibles respuestas a un problema, dependiendo en especial de las características del mismo, y por ello se hace necesario plantear un tipo de escenario adicional que complemente los existentes, el cual proponen llamar escenarios irreales no utópicos.
El presente artículo no pretende anular, corregir, contradecir ni menospreciar la visión de otros autores con relación a los conceptos, usos y utilidad que han propuesto y desarrollado en sus obras con relación a los escenarios que se utilizan en diferentes disciplinas; sólo se limitará a revisar, comparar y argumentar, con base en la experiencia empírica y la contrastación documental los escenarios estudiados hasta el presente y a proponer, con base en el análisis, un tipo de escenario adicional a los ya existentes.
Dada la naturaleza de este trabajo, la metodología utilizada debe ser considerada de tipo cualitativa, con énfasis en la investigación documental, entendiéndose con ello que los datos recopilados provienen de libros, artículos, videos, revistas, publicaciones periódicas y otras fuentes que, a juicio de los investigadores, ofrecen el contenido que se desea contrastar, relacionar y/o vincular al propósito de su investigación.
Para Kahn & Wiener (1968), citado por Martínez (2016), se entiende por escenario a una “serie hipotética de eventos construidos con vistas a sacar a la luz secuencias causales y nudos de decisión”. (p. 10)
Bluet & Zemor (1970), también citados por Martínez (2016), explican que un “escenario es un conjunto formado por la descripción de una situación futura y por la serie de hechos que permiten pasar de la situación original a la situación futura”. (p. 10)
Para Gabiña (1998), citado por Martínez (2016) hay dos tipos de escenarios:
(…) los exploratorios, que parten de tendencias anteriores y presentes y conducen a futuros verosímiles; [y] los anticipatorios o normativos, construidos a partir de imágenes alternativas del futuro, deseadas o temidas, y diseñados de forma «retroproyectiva», dependiendo de si toman en cuenta las evoluciones más probables o las más extremas, pueden además ser tendenciales o contrastados, respectivamente.
(Martínez, 2016, p. 10)
Según Masini & Medina (2000), citado por Vázquez & Ortegón (2006), existen seis escenarios que pueden estudiarse al momento de explorar acciones estratégicas o de tomas de decisión, estos son, de acuerdo a los autores, el escenario tendencial, el escenario optimista, el escenario utópico, el escenario pesimista, el escenario catastrófico y el escenario contrastado.
Por lo general, al establecer los escenarios sólo se estudian tres de ellos, el optimista, pesimista y tendencial.
Se entiende por escenario tendencial aquel que:
(…) trata de mostrar lo que sucederá si las cosas siguen como van. No obstante, no basta con pensar las extrapolaciones de las tendencias que se pueden producir, se requiere explicar cuáles son los factores históricos, o nuevos que influyen o contribuyen a que la tendencia esperada sea similar a la actual, es decir, se necesita precisar aquellos factores que hacen que la tendencia tienda a reforzarse. (Vasquez & Ortegón, 2006, pág. 152)
Se entiende por un escenario optimista aquel que:
“(…) se ubica entre el escenario tendencial y el escenario utópico, ideal o más deseable. El escenario optimista contempla cambios razonables y positivos que no rayan en una ambición desmesurada, basada más en los deseos que en los fundamentos que conllevan los hechos y los datos. El escenario optimista plantea acciones deseables pero plausibles o verosímiles que distinguen aquello que puede lograrse en el corto, mediano y largo plazo” ídem.
Por su parte, se entiende por escenario pesimista aquel que:
(…) contempla un deterioro de la situación actual pero sin llegar a una situación caótica. Es el escenario que se encuentra en medio del escenario tendencial y el escenario catastrófico o aquella situación que empeora dramática y aceleradamente un sistema a causa de factores desestabilizantes, inesperados y descontrolados. Ídem
En lo que respecta a la toma de decisiones y teoría de juegos, los tres escenarios antes explicados toman particular importancia cuando se estudian estrategias como las de Wald, Laplace, Hurwick y Savage.
Tal y como lo expone Vitortiano (2007) las estrategias anteriormente nombradas, también conocidas como criterios, se utilizan cuando se desconocen o ignoran las probabilidades. Explica Vitoriano (2007) lo siguiente:
En la estrategia Wald (pesimista)
“(…) se supone que va a pasar lo peor, y elige aquella alternativa que dé mejor valor. De esta forma se asegura que en el peor de los casos se obtenga lo mejor posible, que corresponde a una visión pesimista de lo que puede ocurrir. En el caso de que los pagos sean costes esta filosofía supone elegir el mínimo de los máximos denominándose minimax, mientras que si son ganancias será el máximo de los mínimos, denominándose maximin”.
(Vitoriano, 2007, p. 7)
Vitoriano (2007) también expoque que la estrategia Hurwicz:
“(…) combina las actitudes pesimista y optimista, valorando cada alternativa con una ponderación entre lo mejor y lo peor posible. Este criterio presenta la dificultad de estimar el valor del índice de optimismo del decisor, de modo que habitualmente se obtiene la solución para todos los posibles valores de este índice y se intenta situar al decisor en alguno de los intervalos resultantes del índice de optimismo”. Ídem.
Y, finalmente, en lo que se refiere a la estrategia Savage, Vitoriano (2007) hace referencia a que:
“(…) toma en consideración el coste de oportunidad o penalización o arrepentimiento por no prever correctamente el estado de la naturaleza. Estos costes de oportunidad se evalúan para cada alternativa y cada estado, haciendo la diferencia entre lo mejor de ese estado y lo que proporciona esa alternativa para ese estado, construyendo la llamada matriz de penalizaciones o costes de oportunidad. Sobre esta matriz se aplican los criterios anteriores, pudiendo aplicarse el del coste esperado, o, lo que es más habitual, el criterio minimax conociéndose entonces también como criterio de minimizar el máximo arrepentimiento”.
(Vitoriano, 2007, p. 7-8).
Como puede observarse, en Teoría de Juegos, se utilizan principalmente los tres escenarios comentados, el pesimista, el optimista y el real o tendencial.
Ahora bien, Gómez, Zuluaga & Hoyos (2009) explican también dos escenarios adicionales, el escenario idealista o utópico y el escenario contrastado.
Al hablar de “escenario idealista o utópico”, los autores hacen referencia a aquel escenario “donde se dan cambios positivos apropiados para generar procesos de refuerzo positivos, comúnmente llamados «círculos virtuosos», los cuales también demandan que se tomen las decisiones que posibiliten esta serie de eventos” (p. 17)
En lo que respecta al escenario contrastado, Vázquez & Ortegón (2006) explican que se trata del escenario:
(…) donde ocurre lo inesperado y reina la incertidumbre, es decir donde abundan los factores de ruptura que quiebran las tendencias existentes en un momento determinado. Sus consecuencias no necesariamente deben considerarse negativas, pues es un escenario que invita a pensar creativamente en nuevas posibilidades para canalizar los hechos positivos o contrarrestar los negativos. Este escenario se reserva para “pensar lo impensable”. El escenario contrastado es importante en la medida en que obliga a pensar que todo puede cambiar abruptamente, sin embargo no es un escenario arbitrario pues debe tener una lógica argumentativa que lo sustente. (Vázquez & Ortegón, 2006, p. 152)
Al revisar los seis (6) escenarios mencionados puede inferirse que los mismos se encuentran asociados a las variables internas y externas principalmente asociado a cambios posibles que pueden ocurrir y, por ende, alterar lo planteado en cada escenario.
Cuando Zuluaga & Hoyos (2009) describen el escenario optimista explican que “es un escenario que puede situarse por encima del Tendencial, pero que no es considerado utópico o irreal“. (p.17), pero al describir el escenario idealista lo asocian con el utópico, omitiendo la palabra irreal en la descripción.
Si se consulta la Real Academia Española (RAE), la palabra irreal, textualmente significa “no real, falto de realidad” [4] por lo que se hace necesario establecer qué se entiende por realidad.
La RAE define realidad como “existencia real y efectiva de algo” [5] al referirse a su primera acepción, por lo que puede inferirse que cuando algo carece de existencia es irreal y que se hace real una vez que existe de manera efectiva.
Ahora bien, la RAE define el término utópico como lo “perteneciente o relativo a la utopía”, [6] y a la utopía como un “plan, proyecto, doctrina o sistema deseables que pa-recen de muy difícil realización”[7]
Es importante destacar que el termino utopía proviene de la obra homónima de Sir. Thomas More (1478-1535). En su artículo TOMAS MORO (1478-1535), Watson (1994) explica que “el término «utópico» se utiliza a menudo para referirse a una idea o un concepto idealista y sumamente deseable pero al propio tiempo totalmente inviable e irrealista” (p. 181)
Una vez aclarados los puntos anteriores, puede establecerse que los autores, para dar nombre al escenario aquí propuesto, han tomado como base los conceptos ofrecidos por la RAE, de los cuales, cómo ya se señaló, puede inferirse que cuando algo no existe, de manera efectiva, ese algo puede considerarse irreal; no obstante, es importante destacar que la inexistencia efectiva de algo no implica la imposibilidad de que pueda llegar a existir.
Por lo tanto, en el consenso, los autores consideran que mientras las condiciones puedan manejarse con los tres escenarios tradicionalmente explorados o bien con los seis escenarios conceptualizados, el séptimo escenario, aquí propuesto, no existe y por ende es irreal, mas, cuando ninguno de los seis escenarios se cumple, cuando ninguno de ellos ofrece una solución al problema, el escenario que se ha decidido denominar “irreal” hace su aparición, especialmente cuando la visión del problema planteado es ampliada, como se explicará más adelante.
Si bien es cierto que la propuesta que realizan los autores podría observarse como “escenarios inicialmente no identificados”, denominarla “escenarios irreales no utópicos” resultó estar más ajustada a la estrategia de divulgación de dicha propuesta.
Así mismo, ya que lo utópico se asocia generalmente con algo inviable, los autores consideran que, cuando las condiciones están dadas para la aparición del séptimo escenario propuesto, éste debe garantizar la viabilidad y materialización de lo que en él se explore y eso lo hace, automáticamente, no utópico.
La propuesta de los escenarios irreales no utópicos surge ante la existencia de soluciones que no están presentes en los elementos que componen los seis escenarios antes nombrados y que, por lo tanto, no se consideran al momento de realizarse un análisis, tomar una decisión o para la proyección de futuras consecuencias, tendencias y/o respuestas a un problema. Al ser estas soluciones, posible y realizables, algo que no existe de manera efectiva en el planteamiento original del problema a resolver, pueden considerarse como irreales si se respeta el concepto emitido por la RAE.
En ese sentido, se propone entender por escenarios irreales:
Aquellos escenarios que contemplan soluciones que no están previstas entre los límites del problema, pero que puedan dar respuesta al mismo, al ofrecer una opción o intervenir en la toma de decisiones al momento de estudiarse, siendo ésta totalmente posible de realizar o concretarse.
También puede decirse que los escenarios irreales no utópicos expanden la visión convencional con la que suele observarse un problema al limitarlo a tres posibles escenarios, como comúnmente se realiza, ampliándolos para así llegar a una respuesta que, no necesariamente será la más óptima pero que debe satisfacer a las partes involucradas.
Adicionalmente, con base en lo expuesto por Gabiña (1998), puede decirse que el escenario irreal no utópico puede considerarse parte de los escenarios exploratorios.
Gaston Berger, citado por Astigarraga (2016), por define a la prospectiva como “la ciencia que estudia el futuro para comprenderlo y poder influir en él” (p.3) y los escenarios tratan de predecir el futuro para, justamente, impactar en él.
Bertrand de Jouvenel, citado también por Astigarraga (2016), propuso el concento el concepto de los futuros posibles o “futuribles”, “es decir que el futuro se puede concebir como una realidad múltiple” Ídem explica Astigarraga (2016) que “en buena medida, la metodología de escenarios y las técnicas asociadas a ella, tan utilizadas en los trabajos de prospectiva, derivan de esta concepción”.
Explica Godet (2007), en concordancia con el concepto de utopía, que todos “los escenarios posibles no son igualmente probables o deseables” (p.11) y que estos dependen en especial del nivel de incertidumbre que se maneje.
Godet (2007) afirma que:
La incertidumbre sobre el futuro puede apreciarse a través del número de escenarios que se reparten el campo de lo probable. En principio este número es más elevado en función de que la incertidumbre sea mayor; pero solo en principio porque es necesario tener en cuenta la diferencia del contenido entre los escenarios: los más probables pueden ser muy próximos o muy contrastados.
(Godet, 2007, p.12)
Y es en esa explicación donde tienen cabida los escenarios irreales no utópicos, debido a que su contenido debe ser considerado muy próximo, lo que lo ubica a este tipo de escenarios en un futuro probable. El cuadro 1 muestra gráficamente lo antes expuesto:

Con base en todo lo anterior, puede decirse que los escenarios irreales no utópicos aquí propuestos se caracterizan por:
-Buscar respuestas verosímiles y posibles a problemas reales, más allá de los límites existentes en dichos problemas.
-Estar orientados a futuros inmediatos, por lo que no contempla cambios abruptos.
-Dar respuestas a problemas con poca incertidumbre o con niveles de incertidumbre manejables.
-Ofrecer una visión ampliada del problema, superando los límites naturales que exponen los escenarios optimistas, pesimistas y reales (conservador o normal) sin que ello signifique obviar su lógica.
-Presentar una respuesta óptima, sin que dicha respuesta sea necesariamente la más óptima.
Dada las características es posible, entonces, comprender que los escenarios irreales no utópicos se orientan a explorar opciones que, en los escenarios tradicionales, no serían posibles de ubicar.
La sustentación de los escenarios irreales no utópicos, puede encontrarse haciendo un símil entre los escenarios aquí explicados y las matemáticas, en especial cuando se estudia la naturaleza y características de los números.
Los escenarios optimistas y tendenciales podrían ser vistos como los números naturales (N), mientras que el escenario pesimista podría compararse con los números enteros (Z), ya que éstos restan; y, finalmente, los escenarios irreales no utópicos podrían compararse con los números racionales (R), ya que éstos poseen una cuantía finita en su extensión decimal, como lo explica Zemeño (s.f.).
Los números naturales y enteros ofrecen soluciones exactas, mientras que los racionales no, pero eso no impide que éstas no sean vistas como soluciones verosímiles.
Ahora bien, para facilitar la comprensión del concepto propuesto de los escenarios irreales, se considera prudente hacer un cuadro comparativo que muestre las orientaciones de los escenarios antes explicados y la propuesta que se hace, destacando las diferencias que existen entre los mismos. Ver cuadro 2.
Como puede observarse en el cuadro 2, los escenarios listados se encuentran circunscriptos a los elementos propios de la visión que se le da al problema, tomando en cuenta los elementos internos y externos que, comúnmente, deben ser explorados en cada uno de ellos, mientras que el escenario irreal no utópico que aquí se propone, está orientado a ampliar esa visión y con ella los límites del problema, de manera verosímil, para encontrar una respuesta que satisfaga a las partes involucradas. Aunque en el cuadro 2 se destacan algunas diferencias, éstas serán ampliadas y explicadas más adelante.

En un problema de Teoría de Juegos, planteado por Debraj Ray (1998) puede ejemplificar el concepto propuesto de los escenarios irreales no utópicos aquí propuestos.
El problema [8] plantea:
Dos parejas viven juntas y cada una tiene que decidir el número de hijos que van a tener. La crianza de los hijos tiene un coste, si son nuestros de “c” unidades monetarias por hijo. Por otra parte, como las dos parejas viven juntas, los hijos de la otra también imponen un coste, éste coste es igual a “d” por hijo ajeno. Tener hijos también genera beneficios, cada pareja sólo obtiene beneficios de sus propios hijos. El beneficio total de tener “n” hijos es igual a A(n). Si cada pareja puede tener como máximo dos hijos. Identifique cada uno de los elementos que componen el juego (Ray, 1998, p. 740).
Al analizar el problema surge la siguiente matriz de pagos. Ver cuadro 3.

Si se asignan valores al azar a las letras propuesta en el problema planteado por Ray (1998), de la siguiente manera: A es 2 veces D. D es ¾ de C. C equivale a 75 [9]. Como C tiene un valor de 75, el valor de D es de 56.25 y eso le otorga un valor a A de 112,5 unidades monetarias.
Al sustituir los números por los valores podemos obtener la siguiente matriz de pagos. Ver cuadro 4.

El análisis que surge es el siguiente:
-Cuadrante 1H; 1H: Si la Familia 1 decide tener 1 hijo y pero la Familia 2 opta por tener 1, ambas familias tendrían el mismo déficit de dinero.
-Cuadrante 1H; 2H: Si la Familia 1 decide tener 1 hijo y pero la familia 2 opta por tener 2, la familia 1 tendría un déficit de 75,5 unidades monetarias mientras la 2 apenas recibiría el 16,74% del beneficio por hijo. Esto se repite de manera inversa en el cuadrante 2H; 1H.
-Cuadrante 2H; 2H: En este caso se observa que de tener 2 hijos cada familia tendrían ambas un déficit de 37,5 unidades monetarias.
La idea de este ejercicio es tomar la decisión más óptima, la cual parece estar ubicada en el cuadrante 1H; 1H aun cuando ambas familias tendrían pérdidas.
Con base en los escenarios antes descritos podría decirse, entonces que, según el caso, el cuadrante 1H, 2H es el óptimo para la Familia 2, mientras que el 2H; 1H es el óptimo para la Familia 1. El escenario 1H; 1H podría ser el escenario conservador o real, mientras que el 2H; 2H no puede ser otro que el escenario pesimista. Véase el cuadro número 5.

Pero, dado los números ¿estaría completo este análisis?
Si ambas familias deciden tener un hijo se verían mermados sus ingresos o no serían sustanciales. En condiciones de desigualdad, teniendo una familia un hijo y la otra dos, la carga para la familia con un hijo sería mayor que la de la familia con dos. Y si ambas deciden tener dos hijos sus finanzas se ven afectadas de manera similar nuevamente; por lo que las opciones que plantea el problema, aunque válidas, no permiten llegar a una solución óptima real, esto debido a que lo que resulta óptimo para la Familia 1 no es óptimo para la familia 2 y viceversa.
Adicionalmente puede observarse en la matriz de pagos existen dos (2) equilibrios de Nash, en el cuadrante 1H, 1H y en el cuadrante 2H,2H.
De acuerdo a Monsalve (2003):
(…) un equilibrio de Nash de un juego es un acuerdo que ninguna de las partes puede romper a discreción sin perder. Es decir, si alguien quiere romper el pacto y lo hace unilateralmente, se arriesga a ganar por debajo de lo que hubiese ganado dentro del pacto. (Monsalve, 2003, p. 140)
Pero, para el problema planteado por Ray (1998), de acuerdo a los valores asignados a las letras, no hay ganancia alguna, en ambos equilibrios se pierde.
Por lo tanto, la solución al problema podría encontrarse si se usa un escenario irreal no utópico.
Este escenario irreal no utópico, correspondería a tomar la decisión de tener cero (0) hijos, dado a que las condiciones, desde el punto de vista económico, no favorecerían a las partes involucradas; lo cual es completamente verosímil y posible de realizar.
Nótese que tener cero (0) hijos no es una opción en el problema, ya que el planteamiento expresa claramente que deben decidir el número de hijos a tener hasta un máximo de dos (2).
Si bien es cierto que el problema no descarta la decisión de cero (0) hijos, no es menos cierto que, en la práctica, la tendencia invita a pensar en uno (1) o en dos (2) hijos, pues, de lo contrario, no se animaría a las parejas ofreciendo un beneficio por hijo, entendiéndose que de no haber hijos no habrá dicho beneficio.
Por lo tanto, el escenario irreal se presenta como ese cuadrante donde se encontrará una respuesta que no está prevista entre las opciones, soluciones y/o salidas a un problema, o bien, no existe de manera efectiva, pero que, de manera directa, representa un beneficio para para los decisores si se explora dicho escenario.
Se hace imperante destacar que no es un escenario viable que una de las dos familias tenga hijos y la otra no, ya que para esta última se convertiría en un gasto adicional, ya que al no tener hijos no recibiría beneficios y tendría que responder ante los costos causados por los hijos ajenos.
El escenario irreal quedaría representado como se muestra en el cuadro 6.
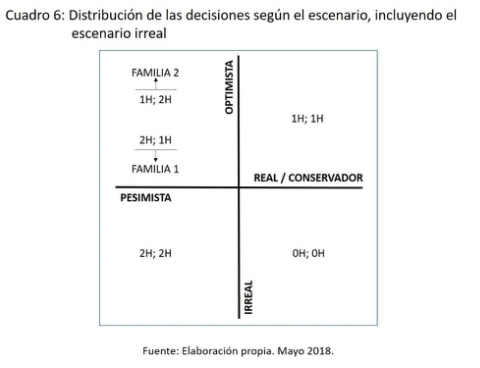
Como puede observarse en el cuadro 5, en un escenario irreal, no utópico, la respuesta al problema pudiera ser no tener hijos, ya que los gastos asociados a la tenencia de los mismos superan los aportes que recibirían por el mismo motivo. No tener hijos, en el momento en que se plantea el problema, es una respuesta verosímil y posible.
La guerra fría, que duró entre 1945 y 1989, mantuvo al mundo entero sumido en los tres escenarios tradicionales.
El escenario real planteaba la coexistencia de Estados Unidos de América y la Unión Soviética en un ambiente de no agresión, mientras que el escenario optimista proponía la existencia de acuerdos entre las partes sin que ninguna de ellas cediera en su ideología. El escenario pesimista, por su parte, suponía el enfrentamiento entre las partes haciendo uso de armamento atómico y devastando buena parte del mundo.
Sin embargo, en 1985 ocurrió un evento no previsto por ambas potencias: Gorbachov propone la «perestroika» el 23 de abril de ese año, en su alocución ante el Pleno del Comité Central del Partido Comunista (Asiain, 1990), cambiando completamente las condiciones socio-políticas existentes e iniciando el fin de la guerra fría.
En este caso, la respuesta ante el problema de la Unión Soviética puede orientarse a un escenario irreal, ya que la orientación política existente desde 1917, según Lozano (2007) descartaba una visión capitalista y democrática como la que existe en el occidente, además la decisión de Gorbachov, al momento de plantear la perestroika distaba de un futuro lejano, por el contrario, el cambio tenía que realizarse a la brevedad.
La respuesta de Churchill frente a Dunkerque es otro caso donde puede observarse un escenario irreal no utópico.
Según Levine (2017), la situación en Dunkerque era dantesca, donde un final feliz era imposible de imaginar, destaca el autor que “al iniciarse la evacuación, la situación militar británica era tan comprometida que, como en la caja de Pandora, solo quedaba la esperanza” (p.26).
Sin embargo, cuando Churchill pone en marcha la «Operación Dinamo», “en la que la armada británica conseguirá evacuar de Dunkerque, entre el 26 de mayo y el 4 de junio [de 1940], a más de 200.000 soldados británicos y más de 100.000 franceses” (Sánchez, 1989, p.222) con la ayuda de embarcaciones civiles, una opción que no estaba prevista en ninguno de los escenarios contemplados al momento de estudiar la realidad que rodeaba Dunkerque.
Aunque poco convencional, la idea de Churchill resultaba arriesgada pero posible y realizable, características éstas propias de los escenarios irreales no utópicos.
Ahora bien, dada la descripción de los escenarios idealistas o utópicos de Gómez, Zuluaga & Hoyos (2009) se puede apreciar que el escenario irreal, aquí propuesto, se diferencia del idealista, ya que éste supone la existencia de cambios positivos para generar procesos de refuerzo positivos, mientras que el escenario irreal persigue la expansión de la visión convencional. Además, basado en el planteamiento de Sir. Thomas More (1478-1535), citado por Watson (1994), cuando hace referencia a la utopía como un planteamiento “deseable pero al propio tiempo totalmente inviable e irrealista” (p.181), se presenta otra diferencia, ya que el escenario irreal no utópico plantea que la respuesta sea completamente posible de materializar.
Así mismo, si se toma en cuenta la descripción del escenario contrastado, explicado por Gómez, Zuluaga & Hoyos (2009), se puede apreciar que éste se diferencia del escenario irreal no utópico propuesto ya que no se trata de dar respuesta a la ocurrencia de lo inesperado y ni se realiza frente a la incertidumbre, por el contrario, el escenario propuesto se orienta a buscar respuestas más allá de los límites del problema, lo que exige conocimiento, certeza y certidumbre.
Si bien es cierto que Vázquez & Ortegón (2006) explican que el escenario contratado “se reserva para «pensar lo impensable», no es menos cierto que lo exponen sobre la premisa que supone que “todo puede cambiar abruptamente” (p. 152), mientras que el escenario irreal no utópico no basa sus planteamientos en cambios repentinos, sino en respuestas que puedan satisfacer las expectativas de las partes involucradas aunque no sean del todo óptimas.
Barker (1985), futurólogo norteamericano, plantea en su video Paradigmas: El negocio de descubrir el futuro, que debemos evitar la «parálisis paradigmática», o bien, pensar sólo existe una única manera de ver y hacer las cosas y exhorta a las personas a ir más allá de los límites de sus paradigmas.
El mismo Barker (1995) nos dice que los paradigmas son patrones o modelos que nos dicen cómo hacer las cosas y, si observamos cómo en varias disciplinas sólo se limitan a estudiar tres (3) escenarios, se podría decir que ello se trata de un paradigma dominante, fuertemente arraigado.
Por lo tanto, el estudio de diferentes escenarios ofrece al decisor y/o a las partes involucradas en un problema convertir los datos que manejan en la información que requieren para tomar una decisión, hacer un movimiento, crear una estrategia o cualquier otro acción que permita dar respuesta a dicho problema, mientras más escenarios se estudien, por inferencia, más cerca se puede estar de una respuesta que pueda considerarse apropiada.
Si bien es cierto que la Teoría de Juegos, las Finanzas y hasta la política, al parecer, suelen concentrar sus análisis a tres escenarios, como lo son el optimista, el pesimista y el real, no es menos cierto que la adición de un cuarto escenario a esa práctica podría significar una ventaja competitiva al momento de realizar un análisis, tomar una decisión o establecer una estrategia.
El escenario irreal no utópico, aquí propuesto, no asegura que la respuesta que se elija frente a un problema sea la más óptima, pero no significa que no pueda alcanzarse una solución que satisfaga las expectativas del decisor al hacer uso de estos escenarios y que, por lo tanto, aun no siendo la respuesta más óptima deje de ser por ello óptima para el momento en que surge dentro de estos escenarios.
La adición de un séptimo escenario, como lo es el escenario irreal no utópico, entendiendo que hay seis escenarios planteados y documentados (tendencial, optimista, pesimista, catastrófico, idealista o utópico y contrastado); pudiera agregar valor a la toma de decisiones y al planteamiento de estrategias si se entiende y se respetan las características propias del escenario propuesto.
A juicio de los autores, todo aquello que sume al momento de estudiar posibles salidas y/o soluciones, sin que resulten inverosímiles o utópicas (irrealizables), puede y debe ser explorado, ya que si se amplía la visión se amplían las posibilidades de encontrar modos satisfactorios y/o aceptables de responder cualquier dilema.
El escenario irreal no utópico, aquí planteado, representa una opción al momento de requerirse una respuesta ajustada a un futuro inmediato y cuyo análisis previo de los tres escenarios tradicionales no ofrezcan soluciones que puedan considerarse ajustadas a la expectativas del problema y que, por ende, no promuevan la adopción de alguna de ellas.
El escenario irreal no utópico pudiera ser una alternativa al momento de buscar soluciones que requieren de objetividad, madurez y liderazgo frente a futuros probables e inmediatos.
Asiain, S. J. (1990). Los efectos de la «perestroika» en el sistema bancario de la Unión Soviética. Claves de la Razón Práctica (págs. 403-420). I.N.D: Academia de Ciencias Morales y Políticas. Recuperado el 15 de mayo de 2018, de http://www.racmyp.es/R/racmyp/docs/anales/A67/A67-23.pdf
Astigarraga, E. (2016). Prospectiva estratégica: orígenes, conceptos clave e introducción a su práctica. Revista Centroamericana de Administración Pública, 13-29. Obtenido de http://prospectiva.eu.
Barker, J. (Dirección). (1985). Paradigmas: El negocio de descubrir el futuro [Película].
Conill, L. Y., Hernández, J., & Chumaceiro, A. (2011). Planificación de escenarios: una herramientaestratégica para el análisis del entorno. Revista Venezolana de Gerencia, 274-290.
Godet, M. (15 de Enero de 2007). Cuadernos de LIPSOR. Prospectiva Estratégica: problemas y métodos. Recuperado el 25 de 05 de 2018, de http://www.laprospective.fr: http://www.laprospective.fr/dyn/francais/memoire/Cajadeherramientas2007.pdf
Gómez, D., Zuluaga, M., & Hoyos, S. (15 de agosto de 2009). Definición sistémica y simulación dinámica de escenarios aplicación a la economía colombiana 2002- 2027. Recuperado el 15 de mayo de 2018, de http://www.ecsim.org: http://www.ecsim.org/Vista/archivos/Metodologia%20y%20Escenarios%20Colombia.pdf
Guillén, R. (s.f.). Teoría de los Juegos - Web del Profesor. Recuperado el 10 de 05 de 2018, de webdelprofesor.ula.ve/...ii/.../teoria_de_los_juegos_completa.ppt
Levine, J. (2017). Dunkerque, la historia que inspiró la pelicula. Nashville: HarperCollins Español.
Lozano, Á. (2007). La guerra fría. Barcelona: Editorial Melusina.
Martínez, S. M. (diciembre de 2016). PROSPECTIVA TERRITORIAL: UNA MIRADA AL CASO PERUANO. Construyendo desarrollo territorial, 8-13. Obtenido de https://www.researchgate.net/publication/311765817_PROSPECTIVA_TERRITORIAL_UNA_MIRADA_AL_CASO_PERUANO
Monsalve, S. (2003). John Nash y la teoría de juegos. Lecturas Matemáticas, 137-149.
Palahniuk, C. (2001). Asfixia. Barcelona: Penguin Random House Grupo Editorial.
Ray, D. (1998). Economía del Desarrollo. Barcelona: Antoni Bosch Editor.
Sánchez, J. A. (1989). Dunkerque 1940. ¿Un error estratégico? La razón histórica, 219-226. Recuperado el 6 de junio de 2018, de http://s4d53ec6797a0383e.jimcontent.com/download/version/1385628819/module/5711308116/name/LRH%2024.16.pdf
Vasquez, J. M., & Ortegón, E. (2006). Manual de prospectiva y decisión estratégica: bases teóricas e instrumentos para América Latina y el Caribe. Santiago de Chile: Naciones Unidas - CEPAL.
Vitoriano, B. (2007). Teoría de la decisión: Decisión con Incertidumbre, Decisión Multicriterio y Teoría de Juegos. Madrid, España: Universidad Complutense. Obtenido de https://repository.unad.edu.co/bitstream/10596/5052/1/212066%20a_dt_UCM.pdf
Watson, K. (1994). TOMAS MORO (1478-1535). Perspectivas, 181-199.
Zermeño, S. D. (s.f.). Sobre los números naturales, reales, imaginarios…. Recuperado el 10 de mayo de 2018, de cienciorama.unam.mx: http://www.cienciorama.unam.mx/a/pdf/316_cienciorama.pdf
1. Ph.D. en Ciencias Administrativas. Magister en Ciencias Gerenciales. Prof. de la Facultad de Negocios y Relaciones Internacionales de la Universidad de La Salle. Email: fsocorro@unisalle.edu.co / felix.socorro@gmail.com
2. PhD en Economía para el Desarrollo / Relaciones Internacionales de la Universidad de Pittsburgh; Profesor Titular de la Universidad del Rosario, Bogotá, Colombia. Email: giovanni.reyes@urosario.edu.co
3. PhD en Ciencias Administrativas y Master of Advanced Studies de la Swiss Management Center University. Profesor catedrático de logística y planeación estratégica. Email: trujillorodri@yahoo.com
8. La idea original de la propuesta surgió con este problema, ya que, al asignar valores al azar a las letras que plantea Ray (1998) se presentó el caso que aquí se expone donde, al parecer, si se seguía la lógica del problema, ninguna familia salía realmente beneficiada sin afectar a la otra.
9. Estos valores fueron asignados sólo como un ejercicio académico y no responden a ningún planteamiento realizado por Ray (1998).