

 Vol. 39 (Nº 43) Año 2018. Pág. 7
Vol. 39 (Nº 43) Año 2018. Pág. 7
Bladismir LEAL 1; Guelvis MATA 2; Sergio MUÑOZ 3
Recibido: 23/04/2018 • Aprobado: 10/06/2018
RESUMEN: Nuestro objetivo es establecer una presentación histórica y geométrica del Teorema de Pitágoras, diferente a la presentación algebraica que suelen realizar un gran número de docentes de educación básica y media, que hace que el estudiante lo olvide rápidamente. Observando el Teorema de forma geométrica, presentamos ejemplos sencillos para motivar en los estudiantes un pensamiento lógico deductivo, sin la necesidad de conocer los números irracionales o calcular raíces cuadradas. También, mostraremos una versión geométrica para triángulos no rectángulos (Acutángulos y Obtusángulos), su historia y ejemplos con números enteros positivos de fácil aplicación. |
ABSTRACT: Our goal is to make a historical and geometric presentation of the Pythagorean Theorem, different from the algebraic presentation that a large number of primary and secondary school teachers usually perform, which makes the student forget it quickly. Observing the Theorem in a geometric way, we present simple examples to motivate in students a logical deductive thinking, without the need to know the irrational numbers or calculate square roots. Also, we will show a geometric version for triangles not rectangles (acute and obtuse triangle), its history and examples with positive integers of easy application. |
El Teorema de Pitágoras forma parte importante de un curso básico de geometría plana, además, es uno de los resultados matemáticos más recordados por los estudiantes de educación media aunque ellos en algunos casos no logran entender su contenido. Recientemente, en encuentros con profesores de educación media, en la Escuela Venezolana para la Enseñanza de la Matemática en 2016 y 2017, pudimos percibir que la gran mayoría de ellos conocían el Teorema de Pitágoras, pero lo enunciaban sin hacer referencias a figuras y lo veían como algo algebraico. En general, poco conocimiento sobre la estructura envuelta en el famoso Teorema; además, reconocieron saber muy poco sobre su historia y demostración. La misma experiencia fue obtenida por uno de los autores Leal Bladismir en los cursos dictados en la Escuela Venezolana para la Enseñanza de la Matemática en los años 2010 y 2011. Los resultados obtenidos de esos encuentros, generó preocupación en los autores quienes decidimos escribir este artículo con miras de poner nuestro grano de arena en la formación de los profesores de educación básica y media.
Hacemos una revisión histórica, para que los profesores adquieran un conocimiento amplio del tema, dejando plasmado un enunciado correcto e histórico del Teorema de Pitágoras, mostraremos un recíproco de dicho resultado, el cual fue usado inclusive muchos años antes que los mismos pitagóricos. Otra pregunta no menos importante, que tiene que ver con triángulos y la relación entre las áreas de los cuadrados construidos con sus lados, es: ¿Se mantiene la relación de igualdad para cualquier triángulo, como la del Teorema de Pitágoras?; Si la respuesta es no, entre las áreas de los cuadrados construidos con los lados de un triángulo, ¿Qué relación existe? El área de un cuadrado construido con un lado de un triángulo ¿Es siempre mayor a la suma del área de los cuadrados construidos con los otros dos lados? O ¿es siempre menor? Aunque son muy pocos los libros que muestran esta inquietud, inclusive entre los artículos consultados no vemos un abordaje a estas preguntas. Parte de nuestro trabajo aquí es responder estas preguntas para darle al docente una visión amplia de lo que sucede con el Teorema de Pitágoras y ¿Por qué esa relación vale solo para triángulos rectángulos?; Además, presentaremos una fórmula en los casos en que los triángulos no son rectángulos. Esto último no es no es una invención nuestra, veremos que ya Euclides en su segundo libro responde a esta pregunta. La forma en que abordamos la versión del Teorema de Pitágoras para triángulos no rectángulos, le da una herramienta al docente para trabajar con áreas y valores enteros, y no con longitudes irracionales, que en muchos casos hace el estudio difícil para el estudiante sobre todo si tiene escaso conocimiento de números irracionales o el nivel donde está siendo enseñado todavía no hay conocimiento para calcular raíces cuadradas.
La metodología utilizada en este trabajo fue desarrollar las inquietudes que obtuvimos de entrevistas realizadas a docentes de educación primaria y media que participaban en la Escuela Venezolana para la Enseñanza de la Matemática, acerca del conocimiento del Teorema de Pitágoras, su historia y resultados relacionados. También, se utilizó una serie de libros de historia de la matemática, es decir, una revisión bibliográfica del tema, para darle un resume al docente desde su orígenes, su creador y cómo ha evolucionado a lo largo de más de 2300 años. Para entender mejor la historia y poder responder a las inquietudes planteadas por los docentes de educación primaria y media, revisamos cuidadosamente los dos primeros libros de Euclides, por medio de una traducción hecha por la Universidad de Clark Massachusetts (2006). También, fueron revisados libros técnicos de geometría y artículos relacionados, para ver las diferentes presentaciones del Teorema de Pitágoras. Una de las preguntas realizadas por los docentes fue ¿Por qué el Teorema vale solo para triángulos rectángulos? Parte de la metodología es desarrollar el trabajo de forma histórica y geométrica para darle respuesta a las preguntas que realizaron los docentes.
El Teorema de Pitágoras tiene una relación muy estrecha con los triángulos rectángulos, lo que significa que, en su descubrimiento los matemáticos de la época ya sabían geometría plana.
El origen sobre el descubrimiento en matemáticas es una parte importante en la enseñanza de las matemáticas, pues hace que los estudiantes e inclusive los profesores, que enseñan matemáticas en nivel básico y medio, tomen mayor interés en aprender de esta disciplina. Hablar de la historia de la matemática en clase o apoyarse, en nuestro caso, en la historia del Teorema de Pitágoras es una herramienta interesante para la compresión de la clase y la convierte en un aprendizaje ameno, y no un aprendizaje técnico o abstracto sin ninguna razón de ser. Meavilla Seguí (2008) sostiene que:
Podemos dar un listado aún mayor de las razones de no dejar de lado la historia de tan importante resultado el cual es objeto de estudio en este trabajo. A menudo los educadores se encuentran con errores matemáticos en la resolución de ejercicios y problemas de sus estudiantes pero hay que incentivarlos para que sigan buscando el camino correcto. Meavilla Seguí, (2008, p 235) relata que: “La historia de las Matemáticas permite dar una visión más humana de dicha ciencia (la Matemática no es obra de los dioses, es el resultado del trabajo de hombres y mujeres que suelen equivocarse). Este hecho puede contribuir a que el alumno no se sienta frustrado ante sus errores y pueda aprender de ellos”.
En esta parte seguiremos de cerca la ideas de (Leal Bladismir, 2010), (Martins Paulo, 2006), (Gonzalez Pedro, 2008) y (Leal Bladismir, 2011). Grecia fue la civilización que dio los primeros pasos firmes en intentar explicar los fenómenos que ocurren en la naturaleza y en particular en las matemáticas, se atrevieron en saber sobre la naturaleza de los números y los objetos (geometría) sin recurrir a los antiguos dioses de la vieja mitología griega. Rompieron con la vieja creencia que todos los fenómenos naturales se debían a los dioses y le dieron paso a los métodos científicos y filósofos. Martins Paulo (2006) afirma que: “los métodos científicos y filósofos que comenzaron a nacer en Grecia muchas veces estaban errados, pero eso no los detuvo en la sed de saber y la búsqueda de conocimiento hizo de Grecia la primera nación en buscar la verdad en todo. La naturaleza para ellos debía ser explicada racionalmente y no a través de dioses ’’.
La matemática no nació con los griegos, ella ya existía en Mesopotamia, Egipto e inclusive en China, pero una cosa es cierta fueron los griegos que le dieron inicio a las demostraciones y deducciones. El trabajo de (Gonzalez Pedro, 2008) dice lo siguiente:
Una tradición muy persistente, que toma como base documental a Plutarco, Vitrubio, Ateneo, Diógenes Laercio y Proclo, atribuye el Teorema de Pitágoras al propio Pitágoras. Pero el examen arqueológico realizado en el pasado siglo de las tablillas de arcilla encontradas en Mesopotamia, pertenecientes a las civilizaciones que se desarrollaron entre los ríos Tigris y Éufrates en el segundo milenio antes de J.C., ha revelado que los antiguos babilonios conocían aspectos del Teorema, más de mil años antes que el propio Pitágoras. Algo similar se puede afirmar respecto de las culturas que aparecieron a lo largo del río Nilo, así como de la antigua civilización hindú y de las antiguas culturas chinas que surgieron en las cuencas de los ríos Yangtze y Amarillo. Pero parece ser que no lo conocían ni las grandes civilizaciones precolombinas de América ni tampoco las del continente africano, exceptuando la egipcia.
A pesar que en otras civilizaciones ya se conocía el Teorema de Pitágoras y además lo usaban para ciertos trabajos prácticos no se le puede quitar el mérito a Pitágoras ya que fue él quien demostró tal resultado para todos los triángulos rectángulos, y no para casos particulares ya conocidos.
Muchos historiadores coinciden con relativa seguridad que Pitágoras nació entre los años 582 a.C. y 569 a.C. en la Isla de Samos, era costumbre en aquella época llamar a una persona por su nombre y el lugar de donde provenía, por eso también era llamado Pitágoras de Samos. Gradolph (1997) afirma:
Con Pitágoras aparece la nueva forma de vida de una comunidad cerrada, aglutinada por reglas comunes de vida y por las mismas ideas sobre el alma y la sociedad. Pitágoras fue el primero que aglutinó en torno a sí un círculo cerrado de discípulos que participaban de su vida y su doctrina…
Con los pitagóricos comenzó un nuevo tiempo en el universo de las matemáticas, su visión mística de los números no les impidió fundar la aritmética como la ciencia de los números. A ellos se les debe las primeras verdaderas demostraciones de la historia. “Entre otros aportes, demostraron, por ejemplo que la suma interna de los ángulos internos de un triángulo mide 180°. En el estudio de los números ellos comenzaron por establecer una primera clasificación en dos categorías, los pares y los impares. También, definieron la media aritmética y geométrica” (Leal Bladismir, 2010, p11-12). La media aritmética y la media geométrica de dos números positivos 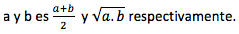
Por supuesto no hemos olvidado, tal vez, su aporte más importante como lo es el Teorema de Pitágoras.
Los Pitagóricos pensaban que toda la naturaleza se podía representar en números, bien sea de forma de números enteros o de forma de números racionales. Pero cuando el triángulo rectángulo con catetos iguales a 1 generó una hipotenusa igual a raíz de 2, trajo una profunda confusión sobre ellos, los números dejaron de explicar todo pues esta extraña diagonal podía ser trazada pero no podía ser medida.
“Se le acredita tal descubrimiento al pitagórico Hipasus de Metapontum (último cuarto del siglo V a.C.), esto produjo una profunda crisis en los fundamentos de la matemática griega y en la escuela pitagórica, pues en su filosofía todo dependía de los números enteros” (Trzaskacz y Hrentchechen, 2017, p3).
(Trzaskacz y Hrentchechen, 2017, p3) Credita-se ao pitagórico Hipasus de Metapontum (último quarto do quinto século a.C.) tal descoberta, sendo que ela produziu uma crise nos fundamentos da matemática grega e na escola pitagórica, pois na sua filosofia tudo dependia dos números inteiros. Traducción de los autores.
El Teorema de Pitágoras trajo el descubrimiento, en aquella época, de los números irracionales, aunque fue con el pasar del tiempo que se llamaron irracionales. Courant & Robbins en su libro ¿Qué es la Matemática? (1955) sostienen que:
Uno de los descubrimientos más sorprendentes de los primeros matemáticos griegos (la escuela pitagórica) fue el de que las cosas no sucedían de modo tan simple. Existen segmentos inconmensurables y, si suponemos que a todo segmento corresponde un número, como medida de su longitud con un segmento unidad, existen también números irracionales. Este descubrimiento fue un acontecimiento científico de máxima importancia. Posiblemente señala el origen de lo que puede considerarse como contribución especifica de los griegos a los procesos rigurosos de las matemáticas… La teoría de lo inconmensurable de Eudoxio, presentada en forma geométrica en los Elementos de Euclides, es una obra maestra de la matemática griega, frecuentemente omitida en las desfiguradas versiones de los Elementos.
Aunque una persona tenga un conocimiento escaso en matemáticas siempre recuerda el nombre de Pitágoras. El enunciado que vamos a presentar es una traducción del libro de Euclides realizado por la Universidad de Clark en su página web www.euclides.org. Este resultado matemático aparece como proposición 47 del primer libro de Euclides. Esta versión o este enunciado del Teorema, es el más popular y el que podemos encontrar en un gran número de bibliotecas de Matemáticas universitarias. Euclides recopiló la matemática del momento y la plasmo en 12 libros, incluyendo la matemática que hicieron los Pitagóricos.
Teorema de Pitágoras: En los triángulos rectángulos el cuadrado del lado opuesto al ángulo recto es igual a la suma de los cuadrados de los lados que comprenden el ángulo recto.
Nosotros lo enunciamos de la siguiente forma: En cualquier triangulo rectángulo, el área del cuadrado cuyo lado es la hipotenusa es igual a la suma de las áreas de los cuadrados que tienen como lados cada uno de los catetos.
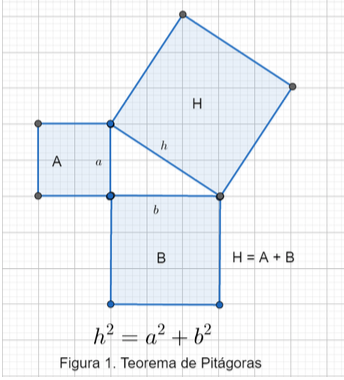
Al observar la figura 1, vemos tres cuadrados diferentes pero el área del cuadrado más grande es igual a la suma de las áreas de los otros dos cuadrados, curioso y verdadero para cuadrados formados por los lados de triángulos rectángulos, es decir, si H denota el área del cuadrado de lado h construido sobre la hipotenusa, A y B denotan el área de los cuadrados construidos sobre los catetos entonces, H=A+B.
Recomendación: si los estudiantes no están habituados con los números irracionales o no han tenido contacto con los números irracionales, la ventaja de ver el Teorema de forma geométrica es, que podemos trabajar con áreas y números enteros positivos. Por ejemplo si los catetos miden a=1 y b=2 respectivamente. ¿Cuál es el área del cuadrado H formado por la hipotenusa? En este caso (manteniendo la notación de la figura 1), el área del cuadrado generado por lado a=1 es , el área del cuadrado generado por el lado b=2 es , entonces el área del cuadrado asociado a la hipotenusa es: H=A+B=4+1=5. Otro ejemplo es, si el área del cuadrado construido por la hipotenusa es igual a H=13 y uno de los catetos mide a=2. ¿Cuál es el área del otro cuadrado generado por el cateto b? En este caso, el área del cuadrado de lado a=2 es entonces, como H=A+B, despejamos B y queda de la igualdad y resulta que B=H-A, sustituyendo los valores de H y A, por lo tanto el área del otro cuadrado es B=13-4=9. Observe que este tipo de ejemplo no necesita del conocimiento de números irracionales y no necesita saber sacar raíz cuadrada de un número.
Recíproco (del Teorema de Pitágoras). Siguiendo la traducción hecha por la Universidad de Clark Massachusetts (2006), el recíproco se enuncia de la siguiente forma:
Si en un triángulo el cuadrado de uno de los lados es igual a la suma de los cuadrados de los dos lados restantes, el ángulo comprendido por esos dos lados restantes del triángulo es recto.
En otras palabras el resultado dicta lo siguiente: Dados tres valores enteros positivos a, b y h. Si entonces, el triángulo construido con lados a, b y h es rectángulo. Por ejemplo, los valores a=3, b=4 y h=5 generan un triángulo rectángulo, pues . En muchas ocasiones usamos este resultado matemático sin darnos cuanta y pensamos que estamos usando el Teorema de Pitágoras y no es así, estamos usando su recíproco. Gonzales Pedro (2008) afirma que:
Los agrimensores egipcios utilizaban el triángulo rectángulo de lados 3, 4 y 5, llamado Triángulo egipcio, a modo de escuadra para trazar líneas perpendiculares. Así nació la profesión de arpedonapta –palabra griega traducción de otra egipcia que significa tendedor de cuerda. Fue precisamente este hecho lo que indujo al gran historiador Herodoto a escribir: " [...] A partir de esta práctica, es como se llegó al conocimiento de la Geometría en Egipto en primer lugar, de donde más tarde pasó a Grecia".
Antes de la existencia del mismo Teorema de Pitágoras los antiguos griegos ya usaban el recíproco de dicho Teorema.
La mayoría de los profesores de educación media con los que tuvimos contacto, en la Escuela Venezolana para la Enseñanza de la Matemática en 2016 y 2017, están conscientes en la deficiencia que tienen en geometría plana. La gran mayoría reconoció no entender la siguiente pregunta ¿Por qué el Teorema de Pitágoras solo vale para triángulos rectángulos? Si consideramos los cuadrados construidos por lados de un triángulo. ¿Cuál es la relación que existe entre las áreas de estos cuadrados construidos? Esta pregunta seguramente se la hizo Euclides 300 a.C. cuando escribía sus primeros libros de geometría plana ya que, en el segundo libro de Euclides aparecen dos resultados que responden a estas preguntas. Estos dos resultados son comunes en algunos libros de geometría, pero poco se mencionan del origen de dicho resultados. En la página web: www.euclides.org donde existe una traducción al español de los libros de Euclides realizada por la Universidad de Clark (2006), podemos observar que tales resultados aparecen con los nombre de proposición 12 y 13 (en el segundo libro) y dictan lo siguiente:
Proposición 12. En los triángulos obtusángulos, el cuadrado del lado opuesto al ángulo obtuso es mayor que los cuadrados de los lados que comprenden el ángulo obtuso en dos veces el rectángulo comprendido por un lado de los del ángulo obtuso sobre el que cae la perpendicular y la recta exterior cortada por la perpendicular, hasta el ángulo obtuso.
Proposición 13. En los triángulos acutángulos, el cuadrado del lado opuesto al ángulo agudo es menor que los cuadrados de los lados que comprenden el ángulo agudo en dos veces el rectángulo comprendido por uno de los lados del ángulo agudo sobre el que cae la perpendicular y la recta interior cortada por la perpendicular hasta el ángulo agudo.
En la proposición 12, triángulo obtusángulo hace referencia a un triángulo con uno de sus ángulos internos midiendo más de 90°, ya que la suma de los ángulos internos de un triángulo debe medir exactamente 180°, significa que los otros dos ángulo deben medir menos de 90° cada uno. La proposición 12 se puede enunciar de la siguiente forma: Dado un Triángulo obtusángulo, el área del cuadrado construido en el lado opuesto al ángulo obtuso (digamos A), es mayor que la suma de las áreas de los cuadrados construidos en los otros dos lados del triángulo (digamos B y C), es decir A > B+C. Observe la figura 2, los lados del triángulo miden a, b y c, donde a es la longitud del lado opuesto al ángulo obtuso. El valor de xc es área del rectángulo que se menciona en la proposición 12, el cual es el comprendido por un lado de los del ángulo obtuso sobre el que cae la perpendicular y la recta exterior cortada por la perpendicular, hasta el ángulo obtuso. Ahora si queremos una fórmula que represente el valor exacto del área A del cuadrado asociado a la hipotenusa a, la proposición 12 expresa que A= B + C +2xc. Como el valor de x no se obtiene de forma inmediata, es mejor trabajar con las áreas y la desigualdad dada anteriormente.
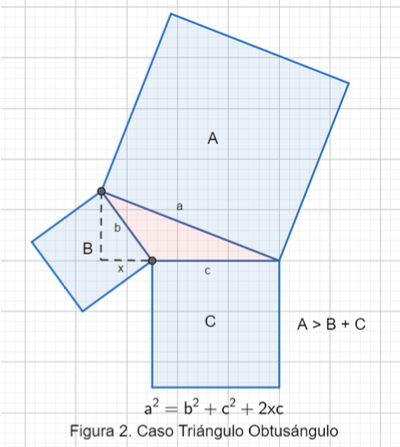
Recomendación: Hacer ejemplos sencillos donde los estudiantes pueden verificar este hecho con números enteros positivos, como por ejemplo: construir triángulos obtusángulos de lados a=5, b=3, c=3 y que el estudiante pueda verificar que es mayor que , entonces 25 > 9+9=18, es decir, A > B + C. También se puede hacer para el triángulo de lados a=6, b= 4, c=3, ya que , por otro lado, B+C= , Note que A > B+C. Otro triángulo obtusángulo es 2, 2 y 3.
En la proposición 13, triángulo acutángulo hace referencia a un triángulo con todos sus ángulos internos agudos, es decir, miden menos de 90° cada ángulo. Caso triángulo acutángulo, el área del cuadrado construido en uno de los lados del triángulo (digamos A) es menor que la suma de las áreas de los cuadrados construidos sobre los otros dos lados (B+C), esto es, A< B+C. Observe la figura 3, el triángulo acutángulo cuyos lados miden a, b y c. El valor cx significa, en la proposición 13, el área del rectángulo comprendido por uno de los lados del ángulo agudo sobre el que cae la perpendicular y la recta interior cortada por la perpendicular hasta el ángulo agudo.
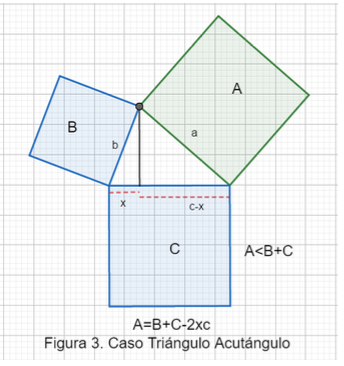
Recomendación: en este caso también podemos hacer ejemplos sencillos usando números enteros positivos, sin necesidad de recurrir a los irracionales o manipular raíces cuadradas. Por ejemplo se puede verificar el resultado para el triángulo de lados a=3, b=3, c=2, ya que y por otro lado . Por lo tanto A< B+C. Considere también el triángulo de lados 4, 5 y 6.
En el estudio pudimos constatar que el Teorema de Pitágoras se conocía mucho antes que lo conocieron los Pitagóricos. También pudimos conocer que los antiguos egipcios usaban el triángulo rectángulo de lados 3, 4, 5 de forma de escuadras para trazar rectas perpendiculares en la construcción, es decir, conocían el recíproco del Teorema de Pitágoras mucho antes que los griegos.
También observamos que gracias al Teorema de Pitágoras apareció con los Pitagóricos por primera vez los números irracionales con el descubrimiento del irracional raíz de 2, el cual trajo mucha confusión para ellos, pero fue uno de los descubrimientos más sorprendentes de los primeros matemáticos griegos (Los Pitagóricos).
En el estudio pudimos descubrir que el Teorema de Pitágoras se remonta a 400 a.c. y que aparece formalmente con el libro uno de Euclides, como proposición de 47, escrito 300 a.c. y que existe una traducción al español de este libro realizada por la Universidad de Clark Massachussets en 2006. También observamos que no es necesario conocer sobre irracionales y sobre raíces cuadradas de los números para poder hacer ejemplos. Usando el área de los cuadrados construidos sobre los lados del triángulo rectángulo, se pueden hacer varios ejemplos sencillos manipulando solo número enteros positivos. Lo que significa que puede ser planteado a estudiantes de educación primaria con un conocimiento mínimo de triángulos, rectángulos y área.
En los casos en que el triángulo no es rectángulo, nos quedan dos tipos de triángulos, Acutángulo y Obtusángulo. En el caso de triángulo acutángulo, podemos ver que el área del cuadrado sobre uno de los lados es menor que la suma de las áreas de los cuadrados sobre los otros dos lados. También, tenemos que, si el triángulo es obtusángulo, el área del cuadrado sobre el lado opuesto al ángulo obtuso es mayor a la suma de las áreas de los cuadrados sobre los otros dos lados. Esto significa que la igualdad vale solo para triángulos rectángulos. Además, nos está dando un método para saber cuándo tres valores positivos generan un triángulo rectángulo, obtusángulo o acutángulo.
Ordenadas alfabéticamente y elaboradas según la guía del siguiente enlace:
Barreto J. (2008) Deducciones del Teorema de Pitágoras a lo largo de la historia como recurso didáctico en el proceso de enseñanza-aprendizaje de la matemática. Números: Revista de la Didáctica de la Matemática N0. 69. Recuperado de: http://www.sinewton.org/numeros/numeros/69/ideas_03.pdf
Courant, R. & Robbins H. (1955) ¿Qué es la Matemática? Una Exposición Elemental de sus Ideas y Métodos. Edición Española Aguilar S.A. Ediciones. Madrid
Gonzalez, P. (2008) El Teorema Llamado Pitágoras. Una Historia Geométrica de 4000 años. Revista de Matemática Sigma No. 32, p 102-130.
Gradolph, T. M. (1997) Biografía de Pitágoras y los Pitagóricos. Recuperado de: http://thales.cica.es/rd/Recursos/rd97/Biografias/12-1-b-pitagoras.html.
Leal, B. (2010) Teorema de Pitágoras. Escuela venezolana para la enseñanza de la matemática. Universidad de Los Andes. Mérida.
Leal, B (2011) Teorema de Pitágoras y sus Aplicaciones. Escuela venezolana para la enseñanza de la matemática. Universidad de Los Andes. Mérida.
Meavilla, Seguí (2008) Revista Sigma. No.32 p 221- 238.
Paulo, M. (2006) Matemática uma Breve História. Vol. 1 Segunda Edicao. Editora Livraria da Física.
Trzaskacz, A. y Hrentchechen. Revista Espacios. Vol. 38, 2017, Número 60, Pág. 2. Recuperado de: http://www.revistaespacios.com/a17v38n60/17386002.html
Universidad de Clarck (2006) Elementos de Euclides 300 a.C. Edición 3.0. Recuperado de: http://www.euclides.org
1. Docente Ocasional Facultad de Ingeniería de la Universidad Nacional de Chimborazo, Ecuador. Profesor Agregado Dpto. de Matemáticas Universidad de Los Andes, Venezuela. lbruiz@unach.edu.ec y bladismir@gmail.com
2. Docente Investigador Facultad de Ingeniería de la Universidad Nacional de Chimborazo, Ecuador. Profesor Asociado Dpto. de Matemáticas Universidad de Los Andes. gemata@unach.edu.ec
3. Profesor Adjunto da Universidade do Estado do Rio de Janeiro, Brasil. sergiomunoz056@gmail.com