ISSN 0798 1015

Vol. 39 (Nº 35) Año 2018. Pág. 4

TEP, matemática y comunicación democrática en educación superior

TEP, mathematics and democratic communication in higher education english

Olga Lucy RINCÓN Leal 1; Mawency VERGEL Ortega 2; José Joaquín MARTÍNEZ Lozano 3

Recibido: 16/03/2018 • Aprobado: 02/05/2018

Contenido

1. Introducción

2. Metodología

3. Resultados

4. Conclusiones

Referencias bibliográficas

1. Introducción

Las tecnologías para el empoderamiento y la participación (TEP), donde los usuarios pueden interactuar y colaborar entre sí como creadores de contenido generado por usuarios en una comunidad virtual al igual que las tecnologías de información y la comunicación han permeado la comunicación digital, ya sea personal o en masas, y representan un movimiento que ha impactado sobre personas distantes (Urry, 2004). La comunicación en estas tecnologías, producto singular de herramientas y redes telemáticas avanzadas, modela relaciones dialógicas entre individuos de la era posmoderna, con implicaciones profundas en los subámbitos educativos (Cardoza- Herrera, Zafra-Tristancho, & Vergel-Ortega, 2016), culturales (Levis, 2009) y de interacción social (Castell, 1995), cambios en el carácter social, que dan lugar a nuevas necesidades e ideas (Fromm, 2000), todo ello en busca de estabilizar las acciones humanas y la generación colectiva y pluricultural de nuevo conocimiento, pero cuyo alcance se limita en el ámbito educativo a relaciones impersonales, temporales virtuales, si no se potencian las herramientas y estrategias didácticas por parte de un orientador o docente.

Un elemento significativo, en el quehacer académico de profesores y para la investigación en educación matemática, es afrontar que un considerable número de alumnos no alcanza los rendimientos esperados en ese tipo de asignatura. Ecuaciones diferenciales es una asignatura del área de matemáticas obligatoria en programas de pregrado, en la cual se presentan altos índices de reprobación debido a inconvenientes conceptuales presentes en los estudiantes que allegan a las universidades, o estudiantes cuyo sistema ha promovido para no presentar bajos índices en sistemas nacionales. De acuerdo Cuevas & Pluvinage (2003), las actividades con el uso de tecnología, deben ser estructuradas implícitamente bajo factores como la acción o importancia que el estudiante ejecute acciones mediante la resolución de problemas específicos, dosificados, a fin de construir conceptos; el problema en contexto, basado en situaciones del entorno del estudiante; el comprobar resultados, analizar nuevamente a la solución general del problema, libertad para planear métodos de solución creando el interés  y con la mínima ayuda del docente, donde los conocimientos adquiridos sean cada vez más complejos, creativos y de participación colectiva con el compromiso de elaborar producciones de diferente formato (Marcelo, y otros, 2014). La motivación por su parte, depende no sólo de factores extrínsecos como la actitud y disponibilidad del profesor para enseñar (Howard, Ma, & Yang, 2016), sino del uso de una didáctica adecuada donde el estudiante desarrolle mediante el uso de la tecnología un contexto real y práctico (Flores, Valadez, & Atencio, 2016; Mendoza, Zermeño, & Zermeño, 2013).

Según Edel-Navarro (2010), este contexto de creación constante de entornos tecnológicos para mejorar el aprendizaje tiene como consecuencia una evolución en los modelos educativos que buscan adaptarse al acelerado avance tecnológico. Así mismo, Rincón, Vergel & Ortega (2015), analizan cómo el uso de la tecnología aumenta la motivación de los estudiantes generando en ellos disposición para aprender matemáticas.

Acorde a lo anterior, los profesores deben aprovechar las ventajas que ofrece la innovación y la realidad social a la cual se enfrentan los jóvenes, siendo los teléfonos inteligentes una herramienta de comunicación permeable con la educación y el desarrollo de competencias en diferentes áreas del conocimiento. Adquirir estas habilidades digitales le ayuda a complementar tareas en el aula (Chacon-Ortiz, Camacho-Gutierrez, & Heredia-Escorza, 2017).  La proliferación de los medios sociales ha creado nuevas alternativas donde los dispositivos móviles (Smartphones y tablets), sin embargo el uso de estos dispositivos móviles puede ir más allá de estas funciones básicas (Cantillo, Roura, & Sánchez, 2012), como se puede observar en  (Lanz, 2014; Forinah & Raimon, 2012 , Vásquez, 2014) donde utilizan los teléfonos inteligentes como un laboratorio portable, estos representan una gran posibilidad para que el aprendizaje sea más accesible, relevante, colaborativo y a su vez  de bajo costo donde se incorpora  en  las universidades con  fines educativos.  Así mismo, el uso de teléfonos celulares por parte de los estudiantes, cada día se encuentra más masificado, donde esta tecnología está logrando un total dominio, lo que implica el manejo de diversas aplicaciones más allá de los usos originales del dispositivo telefónico e incorporar múltiples herramientas de intercomunicación, redes y aprendizaje (Engel & Green, 2011). Burton, Frazier & Annetta (2011)  señalan al respecto que es importante que los profesores universitarios conozcan estos cambios y orienten a sus estudiantes para emplearlo como una herramienta que favorecerá el aprendizaje en procesos de interacción y comunicación intra-aúlicos, de lo contrario se convertirán en una fuente de distracción en el aula de clase (Burns & Lohenry, 2010).

La ventaja de incorporar los aplicativos móviles en el proceso pedagógico es el trabajo colaborativo del estudiante y con la información de interés, donde se desarrollan grandes potencialidades para mejorar los procesos pedagógicos donde se fomentan el desarrollo de competencias básicas, destrezas y habilidades propias de la era digital (Sepulveda, Trejos, Arango, Bustos, & Arias, 2013).  Es así como Cuevas, Rodriguez & Gonzalez (2015) introdujo el concepto de derivada de una función real en un primer curso de cálculo diferencial a nivel superior. Se tomaron elementos del desarrollo histórico conceptual del cálculo, la aplicación de una ingeniería didáctica en particular y de manera importante el empleo de la tecnología digital. Los resultados obtenidos fueron alentadores, porque se logró que la mayoría de los estudiantes alcanzaron con éxito un grado de comprensión conceptual y operativa del concepto de derivada de una función real. Lo anterior fue uno de los factores que condujo a elevar sustancialmente el índice de aprobación, lo cual ayudó a solventar problemas de deserción en la universidad donde se experimentó, pero sobre todo a una mejor comprensión del concepto de derivada de una función real por parte de los estudiantes.

 De otra parte, Rincón & Vergel (2015) diseñaron una encuesta donde se evaluó un modelo de calidad de servicio en la enseñanza del cálculo integral a través del uso de blogs.  Las dimensiones del estudio corresponden con el modelo de calidad de servicio Servqual. Se plasmaron los perfiles de los estudiantes en función de las dimensiones del modelo evaluado, encontrando que el factor predominante con un 44% de variabilidad es la percepción de disponibilidad constante y completa de una gama de recursos didácticos como de contenidos.

En esta investigación se encontró con que el uso de la tecnología aumenta la motivación de los estudiantes generando en ellos disposición para aprender matemáticas. El blog fomenta el autoaprendizaje porque facilita la comprensión de conceptos y procedimientos que requieren dedicación y tiempo, con ello el estudiante refuerza y puede avanzar de acuerdo a su disponibilidad.

Teniendo en cuenta lo anterior la investigación planteó resolver ¿Cómo promover una mejor comprensión de los conceptos matemáticos en ecuaciones diferenciales, a través de herramientas didácticas mediadas por tecnologías para el empoderamiento y la participación (TEP)?

2. Metodología

La investigación siguió un enfoque cuantitativo, con diseño cuasi-experimental de tipo campo, donde se implementan herramientas, actividades didácticas y se aplican instrumentos Pretest y Post-test, apoyada en el enfoque cualitativo con método fenomenológico. A partir de una muestra seleccionada se buscó analizar el rendimiento académico, habilidades y competencias e identificar percepciones y determinar necesidades en estudiantes que utilizaron aplicativo móvil interactivo, en función de las características y variables objeto de estudio.

Se tomó como universo poblacional las comunidades virtuales digitales correspondientes a dos multimedios on line, de Venezuela y Colombia respectivamente, con diversas tradiciones de orden cultural, comunicativo, social, y tecnológico pero atravesadas por el vector común de la participación interactiva de usuarios integrados a una plataforma digital, procediéndose a seleccionar muestras representativas de estudiantes que utilizan redes de comunicación disponibles en las páginas web de profesores de instituciones educativas y usuarios de dispositivos móviles. La elección de países referidos estuvo fundada en criterios básicos de naturaleza estructural y de carácter episódico. El primero, acorde a las similitudes de un conjunto de patrones culturales, lingüísticos y comunicacionales que ambos países comparten y que reconocen una raíz común. El segundo, referido al emergente temático objeto de la investigación que floreció en el campo comunicacional como respuesta directa y espontánea a situaciones de crisis políticas y económicas.

La población estuvo conformada por estudiantes de diferentes Facultades, matriculados en asignaturas de ecuaciones diferenciales. El método de ajuste en el muestreo fue el método de ajuste de Politz y Simmons diseñado para disminuir los sesgos presentes en el test dado que no todos los participantes tienen la misma probabilidad de aparecer en la muestra; el análisis de varianza permitió determinar si existen diferencias estadísticamente significativas entre los grupos.

La muestra estuvo conformada por 163 estudiantes, el 57,1% de género masculino con edades entre 17 y 20 años, un 39,7% de género femenino con edades entre 21 y 24 años y un 3,2 % con edad superior a 25 años. La edad promedio del grupo fue de 20.13 años con una desviación estándar de 2,34 años.

Considerando los programas en forma particular, el programa con mayor representación fue el de biotecnología con un 27%, seguidos por los programas de ingeniería que en conjunto representan más del 65% de la muestra, y dentro de ellas, sistemas y civil, con 23% y 22% respectivamente. Los estudiantes de otros programas (veterinaria, zootecnia o pecuaria, industrial y agroindustrial) representan una minoría que no alcanza el 5%.

Se avanzó en un estudio comprensivo de la compleja y dinámica relación poder-comunicación desde las perspectivas teóricas de redes y sistemas complejos tomando como categoría central el concepto de ciudadanía digital reflejado en los espacios y foros virtuales seleccionados como unidad de análisis, se desagregó esta variable en tres dimensiones básicas donde se reconoce y manifiesta la participación cívica on line; a saber: cognición, relación, y participación. Acorde a la naturaleza del fenómeno derivado de la articulación entre comunicación, educación en el entorno de las redes digitales, resultado de la interacción dinámica de los complejos cognitivo, vincular y pragmático, se diseñó un esquema matricial el desarrollo teórico de los conceptos, categorías, recursos e interacciones para una adecuada interpretación del alcance y significado de las relaciones que se ponen en juego en la comunicación democrática de carácter multimodal.

Variables causales consideradas fueron recurso con indicador discurso dominante, mensaje, afinidad; ilocutiva con indicador interacción; creatividad con indicador cultura digital, creación de contenido, interactividad; variables dependientes habilidades con indicador conocimiento, comunicativas, interacción social; competencias con indicador resolución de problemas, aplicación de conocimiento.

 Referente al material didáctico, se diseñó aplicativo móvil “Ecuadif”, el cual contiene aplicaciones de las ecuaciones diferenciales, conceptos, módulo de generación de ecuaciones y diseños de prototipos elaborados con apoyo de los estudiantes. Para el diseño del aplicativo móvil se requirió de conocimientos básicos de lenguaje XML (necesario para el diseño de las interfaces gráficas que aparecen en el App) y lenguaje Java (necesario para programar las funciones de la App y enlazar éstas con las interfaces). Las características de la App estuvieron conformadas por seis archivos con extensión .XML y nueve archivos con extensión Java.

Instrumentos implementados como foros y guías estructuradas permitió identificar percepciones de los participantes con respecto al cumplimiento de competencias y habilidades en ecuaciones diferenciales, así como detectar necesidades al utilizar un aplicativo móvil. La guía didáctica se abordó como un instrumento adecuado para el docente como herramienta estratégica y al estudiante para la mejor comprensión, asimilación de conocimientos; la componen los elementos: nombre de la unidad, tema de las aplicaciones de las ecuaciones diferenciales, las competencias a desarrollar (cognitiva, comunicativa, habilidades y destrezas de la disciplina, proceso de aptitudes socio afectivas); marco conceptual de la aplicación de la ecuaciones diferenciales, ejemplos y análisis de situación donde se utiliza los aplicativos móviles con las ecuaciones diferenciales, videos, modelado de ecuaciones. Análisis estadísticos correspondientes para el pre test y post-test permitieron determinar diferencias significativas en rendimiento académico, cuyo test tuvo fiabilidad alta (alfa de Cronbach =0,91).   Para el desarrollo de la validez de contenido, en el análisis cuantitativo se utilizó el método de índice de validez de contenido nivelado o promedio, con una escala ordinal, teniendo en cuenta los criterios de relevancia y pertinencia. El análisis cualitativo se realizó por medio de la síntesis de las observaciones, con una muestra de 11 expertos de instituciones de educación superior con formación doctoral, El instrumento guía estructurada, tuvo una validez facial disminuida con expertos en el área, debido a que los expertos lo calificaron con un índice de acuerdo de 0,79; una validez facial calculada elevada con un índice de acuerdo de 0,88 y una validez de contenido elevada, con un índice de validez de contenido de 0,85. El análisis de la información se realizó a través el software SPSS y Nvivo. El registro se hizo respetando la naturaleza de la medición de cada una de las variables, así como también se seleccionaron las técnicas de análisis descriptivos adecuados para cada una de ellas.

Características de software

La propuesta basada en TEP incorporó el diseño e implementación de una estrategia didáctica para la enseñanza de ecuaciones diferenciales con el objeto de mejorar rendimiento y competencias en el área de matemáticas en estudiantes de ingeniería a través de aplicaciones de ecuaciones diferenciales utilizando como herramienta los aplicativos móviles, visualizando y conectando en forma dinámica.  La App Ecuadif abarca hasta el momento 6 archivos con extensión .XML y 9 archivos con extensión.JAVA, cuyo fin es:

Splash.xml: mantiene la interfaz gráfica que muestra el logo principal de la App, este tipo de interfaces tiene el nombre de “Splash screen”,

Welcome.xml: mantiene interfaces gráficas relativas al primer uso de la App, da a conocer a la las funciones de la App.

Home.xml: mantiene la interfaz gráfica principal de la App, permite observar los casos disponibles en la App para el aprendizaje de la solución de diferentes tipos de ecuaciones diferenciales.

Description.xml: mantiene la interfaz gráfica en la cual se detalla un enunciado y la deducción de la ecuación característica.

Example.xml: mantiene la interfaz gráfica relativa a la descripción de los ejemplos correspondiente a cada tema del contenido programático, es decir, aquí se describe la problemática y su solución paso a paso.

Graph.xml: mantiene la interfaz gráfica relativa a la muestra de la gráfica correspondiente a cada problema.  Cada uno de estos archivos está asociado directamente a su correspondiente archivo con el mismo nombre pero con extensión .JAVA, que se encargará de almacenar, recibir o preguntar al usuario cualquier dato necesario.  La guía se estructuró de acuerdo con el contexto teórico, ejemplos y a su vez la implementación del uso del aplicativo móvil. 

3. Resultados

Análisis cuantitativo muestra que un 87.3 % de los estudiantes poseía un dispositivo móvil (tabla 1). El 65% del conjunto cursaba la asignatura de ecuaciones diferenciales por primera vez y no tenía la condición de repitiente, un 25 % cursaba la asignatura por segunda o tercer vez.  El 89% procedían de instituciones de carácter oficial, estrato socioeconómico dos y tres. El índice de rendimiento promedio por programa de los estudiantes fue de 3,43 puntos con una desviación típica aproximada de 0,35 puntos y un intervalo de confianza del 95% la media osciló entre 3,34 y 3.51 puntos.  El 50% de los estudiantes tiene calificaciones superiores a 3.4 puntos. La diferencia entre el estudiante que tiene mayor puntaje (4.48 puntos) y el de menor puntaje (2.91 puntos) equivale a 1,57 puntos. El 50% de los estudiantes tiene índices promedios comprendidos entre 3.16 puntos (percentil 25) y 3.59 puntos (percentil 75). El cociente entre el coeficiente de asimetría entre su respectivo error estándar (0,87/0,30) e superior a 1,96 indicando que la distribución se aleja de la normalidad.

Tabla 1
Características del grupo

Fuente: Autores

Con respecto a la evaluación realizada en la fase del pretest el promedio es único en 3,13 puntos con alta variabilidad en los resultados reflejados en una desviación típica de 0,96 puntos. El intervalo de confianza del 95% para la media osciló entre 2,89 y 3,37 puntos. El 50% del grupo obtuvo puntuaciones de 3,5 puntos o menos. La diferencia entre el que mayor puntaje obtuvo (4,5 puntos) y el que menor puntaje alcanzó (2,0 puntos) fue elevada y alcanzó los 2,5 puntos. El cociente entre el valor del índice de Curtosis, que evalúa la forma de la distribución, y su respectivo error estándar (-1,52/0,59) fue superior en valor absoluto a 1,96 lo cual indicó que los datos se alejaron de la normalidad. Estos resultados permiten aseverar que las condiciones académicas del grupo al iniciar la experiencia de investigación fueron muy heterogéneas, existiendo estudiantes con altos promedios y conocimientos sobre los temas tratados y otro grupo de estudiantes con dificultades académicas serias ante los temas evaluados. No se evidenció dependencia ni relación causal de variables género y edad de los estudiantes en el rendimiento, ni asociación entre estas variables con frecuencia y uso del aplicativo móvil.

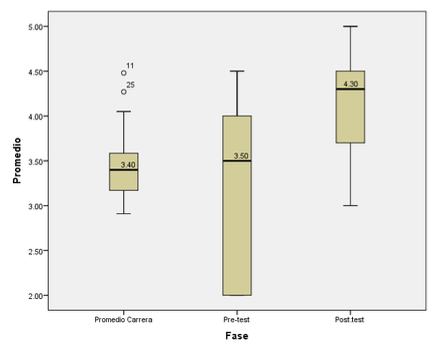
En referencia a la evaluación en la fase del post-test (figura 1), los resultados evidenciaron un mejor rendimiento con un promedio alto de 4,18 puntos y menor variabilidad (DT=0,58) en comparación con los promedios de la carrera o programa académico cursado y de la fase del pretest. El intervalo de confianza para la media en esta fase se ubicó entre 4,02 y 4,32 puntos. El 50% del grupo alcanzó puntaje superior a 4,3 puntos. La diferencia entre el puntaje máximo (5 puntos) y el de menor puntaje (3 puntos) fue de dos puntos, lo cual evidencia rendimiento superior en comparación con las fases anteriores.

Por otra parte, se evidencia puntajes superiores al considerar el intervalo entre el percentil 25 y el 75, que alcanzan valores comprendidos entre 3,7 y 4,5 puntos respectivamente. Los valores de los índices de asimetría y de la forma (Curtosis), divididos entre sus respectivos errores estándar, (-0,275/0,302=0,91) para asimetría y   (-0782/0,59=-1,32), ambos en el intervalo de ±1,96 indican que la distribución de los resultados en la fase del post-test se aproxima a la normalidad.

El diagrama de caja, mostrado en la figura 1, permite observar la relación a nivel descriptivo del promedio de la carrera y los resultados de la evaluación en ambas fases.  Existen dos puntos a destacar sobre la base de este diagrama: a) La existencia de valores extremos en el promedio de la carrera y la prueba pretest que se refleja en mayor variabilidad y que es reducido sustancialmente en la fase del post-test y b) mayor promedio en ambas fases en comparación con el promedio de la carrera y que se acentúan más, posterior a la intervención del docente a partir de la aplicación de la estrategias con el dispositivo móvil, es decir en la fase del post-test cuyo rendimiento supera en promedio los 4 puntos.                                                        

Figura 1
Diagrama de Caja con valores descriptivos del promedio de la
carrera y los resultados de la evaluación en ambas fases.

Fuente: Autores

Considerando estas 3 fases (1: Promedio de la carrera, 2: Evaluación Pretest y 3 Evaluación Post -test) como una variable categórica o factor y el promedio como una variable numérica dependiente, ¿Podemos hablar de diferencias estadísticamente significativas entre estos grupos? El resultado de la prueba F=39,73 con un  p-valor=0,00<0,05 permite rechazar la hipótesis de igualdad de promedios y concluir que existen diferencias significativas entre las distintas fases, permitiéndose concluir de esta forma la efectividad de la intervención en el proceso de enseñanza a partir de las estrategias implementadas en el aula por medio de la incorporación del aplicativo móvil en el proceso didáctico y recurso de aprendizaje en la enseñanza de las aplicaciones de las Ecuaciones Diferenciales (Tabla 2).

Tabla 2
ANOVA de un factor, considerando la fase de la
evaluación y el rendimiento promedio en cada fase.

Fuente: Autores

Análisis de las valoraciones cualitativas manifiestas en foros por parte de los estudiantes acerca de la utilización de los aplicativos móviles en la solución y generación de modelos en ecuaciones diferenciales, consideraron principalmente dos aspectos, el primero relacionado con los objetivos del aplicativo móvil dentro del contexto de la asignatura ecuaciones diferenciales y cómo son percibidos por los estudiantes. Destacaron características referidas a la comprensión de los temas de mayor complejidad con el uso de herramientas que facilitaron el desarrollo de la asignatura y el uso efectivo del aplicativo móvil en la solución de situaciones problema.

Figura 2
Objetivos alcanzados a través del aplicativo
móvil, según la perspectiva del estudiante

Fuente: Autores                   

Entre el conjunto de valoraciones que realizaron los estudiante sobre la experiencia de aprendizaje en los temas de las aplicaciones de ecuaciones diferenciales al hacer uso de los aplicativos móviles, un 36,5% destacó su utilidad para comprender los temas complejos, si a este hecho se le suma la aplicabilidad encontrada para resolver problemas donde se utilicen las ecuaciones diferenciales, un 60% los estudiantes considera que la aplicación promovió el aprendizaje significativo en conceptos abstractos de la asignatura. En segundo término, se destacó el soporte que dio la herramienta para resolver problemas relacionados con situaciones cotidianas, siendo este aspecto mencionado por un más del 20% de los estudiantes. Un 85% del grupo asoció la utilidad de la aplicación para definir y relacionar variables inmersas en la situación problemática planteada.

En cuanto al conjunto de bondades y preferencias encontradas por los estudiantes al momento de utilizar el aplicativo móvil, son muy variadas, más del 70% del grupo resalta dos aspectos fundamentales: la metodología paso a paso con soporte gráfico (42.9%) y, el amplio contenido de teoría, ejemplos y ejercicios para resolver. Estas valoraciones sin duda fortalecen y validan la iniciativa de innovación en el aula, por parte del docente; los estudiantes aprecian el detalle de la metodología para resolver los problemas, que muchas veces en las aulas de clases les cuesta visualizar y además reconocen mayor amplitud de los conceptos, contenidos y ejemplos de los cuales disponen para prepararse mejor para las evaluaciones de la asignatura. Otras características como la calidad de los ejemplos y el uso de videos tutoriales, también fueron valoradas positivamente. Categorías emergentes fueron recurso didáctico, comodidad y accesibilidad.

La infraestructura hizo referencia al conjunto de elementos y relaciones que conformaron la matriz subyacente que encauzó los flujos emergentes del proceso comunicativo, social y facilitó la comunicación sincrónica o asincrónica. En esta categoría se resaltó la sinergia y el agrupamiento espontáneo de los participantes en comunidades virtuales para la solución de problemas, heterogéneas en sus composiciones internas pero homogéneas en su patrón funcional, llevándoles a conformar un conglomerado autónomamente organizado.

Categorías emergentes que surgieron fueron la interacción y colaboración entre sí como creadores de contenido en una comunidad de aprendizaje virtual, es decir se posiciona la herramienta App dentro de las tecnologías para el empoderamiento y la participación TEP, como propuesta pedagógica en la enseñanza de ecuaciones diferenciales u otras áreas de la matemática (PP)  surgen categorías en torno a características como contextualizada (CT), didáctica (D), y fomentan el desarrollo de habilidades (H). Con implicaciones de fácil lectura y recordación a partir de gráficas y representaciones adecuadas, y con problemas aplicados en ingeniería y economía, el desarrollo de habilidades manifiestas en relacionar ecuaciones diferenciales con problemas reales, comunicar el aprendizaje y comunicación basada en el pensamiento crítico(tabla 3).

La comunicación democrática (C) (tabla 4), con profundidad en los indicadores recurso metafórico (RM), comportamiento social (CS), empatía (E). Finalmente las habilidades metacognitivas (HM) (tabla 5). Manifiesta en indicadores conocimiento (CN), estrategias (ES), competencias en matemáticas (CM) y comunicación creativa (CC).

Tabla 3
Análisis Unidad Temática 1.  Elemento referencial categoría deductiva

Fuente: Autores

----

Tabla 4
Análisis Unidad Temática 2. Elemento referencial

Fuente: Autores

-----

Tabla 5
Unidad Temática Nº 2: Habilidades meta cognitivas

Fuente: Autores

A partir del análisis es posible teorizar en torno a comunicación democrática y  habilidades metacognitivas para el aprendizaje de ecuaciones diferenciales en estudiantes: “La propuesta pedagógica basada en la implementación de aplicativos web y móviles, en el marco de las tecnologías para el empoderamiento y la participación, fomentan la comunicación democrática y permiten el desarrollo de habilidades metacognitivas para la generación de conocimiento, la planificación de estrategias de solución de problemas y el desarrollo de competencias de representación, interpretación, aplicación y comprensión matemática”.

4. Conclusiones

El complejo global de las tecnología para el empoderamiento y la participación se orientó hacia un propósito la comunicación democrática como forma de expresión resultante del diálogo social, configurada mediante un proceso de retroalimentación acumulativa y sinérgica entre los actores a través de herramientas tecnológicas y aplicativos web ( Flórez, y otros, 2017), en una configuración espacio temporal que posibilitó la interacción, la participación, la generación de contenido, la regeneración y la transformación constante del conocimiento.

La incorporación de las nuevas Tecnología con los aplicativos móviles en la enseñanza de las Ecuaciones Diferenciales mostro como el estudiante toma una actitud positiva hacia su utilización donde se logra complementar los conocimientos necesarios para comprender y mejorar sus clases , generando en los estudiantes disposición para aprender las matemáticas.

Con la ayuda del aplicativo móvil el alumno comprende más fácil los conceptos básicos de las aplicaciones de las Ecuaciones Diferenciales donde el explora, interpreta, deduce, justifica y las desarrolla, logrando así un favorable rendimiento académico como lo observado en la investigación (Vergel, Martinez, & Zafra, 2015).

La utilización de las Nuevas tecnologías rompe con los esquemas tradicionales de enseñanza, donde se fomenta el aprendizaje autónomo siendo el profesor un facilitador de acuerdo a los recursos tecnológicos disponibles donde los alumnos se forman tecnológicamente según lo expuesto por (Cabero & Llorente, 2011; Rincón Leal O. L., 2016), convirtiéndose el aplicativo móvil un recurso didáctico extremadamente favorable.

El hecho de utilizar las NTIC en el desarrollo de los contenidos en la asignatura de Ecuaciones Diferenciales promueve en el estudiante al trabajo independiente donde este es participe de su propio aprendizaje y  adquiere habilidades para el cálculo de acuerdo con (Ruiz, 2014), donde esta herramienta ayuda a complementar el trabajo docente, desarrollando así las competencias propias del área.

Se evidencia la importancia atribuida por los estudiantes al uso del aplicativo móvil donde representa un apoyo para comprender los temas complejos, destacándose la aplicabilidad encontrada para resolver problemas donde se utilicen las ecuaciones diferenciales promoviéndose así un aprendizaje significativo en la asignatura , favoreciendo la comunicación con sus compañeros de acuerdo con lo expuesto por (Ortiz, Quintero, & Díaz, 2015).

La utilización del NTIC en contextos reales, mejora la calidad didáctica de las clases recibidas (Parra & Dìaz, 2014) y disponibilidad de recursos alternativos para la enseñanza, que se traducen en un mejor rendimiento académico de los estudiantes (Sabogal, Monroy, Landero, & Molina, 2015) solidificando la intervención curricular de la asignatura con otras afines en el currículo, siendo un aporte significativo al perfil profesional del estudiante, como también lo manifiesta (Vergel, Rincón, & Martínez, 2016) .

De acuerdo con (Guacaneme & Mora, 2011; Muñoz, 2012), el docente debe adquirir una metodología un cambio de actitud hacia la enseñanza donde el estudiante es artífice de su propio aprendizaje trabajando, reflexionando y elaborando sus propios procesos del pensamiento. Por esto la incorporación de los aplicativos móviles en el aula de clase permite al estudiante hacer un seguimiento de los temas paso a paso donde se va enriqueciendo a medida que realiza la interacción colaborativa (Ramos, Herrera, & Ramírez, 2010) y lúdica donde se fortalece el desarrollo del proceso de aprendizaje, mejorando sus competencias (Vargas, Gómez, & Gómez, 2013) .

La inclusión de los dispositivos móviles en el proceso didáctico como recurso de aprendizaje en la enseñanza de las Ecuaciones diferenciales busca innovar en este proceso colocando al alcance del estudiante un complemento educativo en el aula de clase con el uso de las herramientas tecnológicas, que emplean de manera cotidiana. 

Apoyos

El artículo es resultado del proyecto de investigación “Aplicativos Móviles en la Didáctica del Cálculo”  financiado por el fondo FINU de la Universidad Francisco de Paula Santander, Contrato Nº 023-2016

Referencias bibliográficas            

Burns, S., & Lohenry, K. (2010). Cellular Phone use in Class:Implications for Teaching and Learning a Pilot Study. College Student Journal, 44(3), 805-810.

Burton, E., Frazier, W., & Annetta, L. (2011). Modeling Reality Games with Preservice Elementary and Secondary Science Teachers. Journal of Technology and Teacher Education, 9(3), 303-329.

Cabero, J., & Llorente, M. (2011). Percepciones del profesorado universitario hacia las acciones formativas apoyadas en la Red. Profesorado.Revista de Curriculum y formación del profesorado, 15(1), 211-221.

Cantillo, C., Roura, M., & Sánchez, A. (2012). Tendencias actuales en el uso de dispositivos móviles en educación. La Educ@ción Digital Magazine, 147, 1-21.

Cardoza- Herrera, C. A., Zafra-Tristancho, S. L., & Vergel-Ortega, M. (2016). Comunidades de aprendizaje, su impacto desde el lenguaje para la construcción de conocimiento matemático. Bogotá: Grupo Editorial Ibañez.

Castell, M. (1995). The Informational City: Information Technology, Economic, Restructuring and the Urban Regional Process. Madrid: Alianza.

Chacon-Ortiz, M., Camacho-Gutierrez, D., & Heredia-Escorza, Y. (2017). Conocimientos sobre aprendizaje móvil e integración de dispositivos móviles en docentes de la Universidad Nacional de Costa Rica. Revista digital de Investigación en Docencia Universitaria, 11(1), 146-162. doi:10.19083/ridu.11.507

Cuevas, C., & Pluvinage, F. (2003). Les projets d'action practique, elements d'une ingeniere d'ensigment des mathematiques. Annales de didactique et de sciences cognitives, 8, 273-292.

Cuevas, C., Rodríguez, A., & González, O. (2015). Introducción al concepto de derivada de una función real. (CINVESTAV-I.P.N., Ed.) El Cálculo y su enseñanza, 5. Septiembre 2013-Septiembre 2014, 157-164.

Edel-Navarro, R. (2010). Entornos virtuales de aprendizaje : la contribución de lo "virtual" a la educación. Revista Mexicana de Investigación Educativa , 16(14), 7-15.

Engel, G., & Green, T. (2011). Cell pones in the Classroom: are we Dialing up Disaster? Tech Trends:Linking Research and Practice to Improve Learning, 55(2), 39-45.

Flores, I., Valadez, S., & Atencio, A. (2016). La Didáctica de la matemática en contexto, promotora de la motivación matemática en ecuaciones diferenciales. Electrónica, Humanidades, Tecnología y Ciencia, 14(1), 1-5.

FLÓREZ, Marcela., AGUILAR, Andrea, J., HERNÁNDEZ, Yurley, K. , SALAZAR, Juan, P., PINILLOS, Jesús ,A.,PÉREZ, Carlos, A. Sociedad del conocimiento, las TIC y su influencia en la educación. Revista Espacios.Vol 38, Año 2017,  Número 35, Pág. 39. Recuperado de: http://www.revistaespacios.com/a17v38n35/a17v38n35p39.pdf

Forinah, & Raimond. (2012). Smartphones as portable oscilloscopes for physics labs. The Physics Teacher, 50, 242-243.

Fromm, E. (2000). El miedo a la libertad. Buenos Aires : Paidós.

Guacaneme, E., & Mora, L. C. (2011). La educación del profesor de matemáticas como campo de investigación. Papeles, 3(6), 18-25.

Howard, S., Ma, J., & Yang, J. (2016). Student rules: exploring patterns of students computer-efficacy and engagement with digital technologies in learning. Computers & Education, 101, 29-42. doi:10.1016/j.compedu.2016.05.008

Lanz. (2014). Familiarizing Students with the Basics of a Smartphone’s Internal Sensors. The Physics Teacher, 52, 557-559.

Levis, D. (2009). La pantalla ubicua: televisores, computadoras y otras pantallas. Buenos Aires: La Crujía.

Marcelo, C., Yot, C., Mayor, C., Moreno, M., Murillo, P., Rodriguez, J., & Pardo, A. (2014). Las actividades de aprendizaje en la enseñanza unversitaria:¿hacia un aprendizaje autónomo de los alumnos? Revista de Educación(1), 334-359.

Mendoza, L., Zermeño, M., & Zermeño, R. (2013). Desarrollo de habilidades cognitivas y tecnológicas con aprendizaje móvil. Revista de Investigación Educativa de la Escuela de Graduados en Educación, 3(6), 30-39.

Muñoz, S. (2012). Aportes didácticos de las Nuevas Tecnologías en Matemáticas: calculadoras, ordenadores, internet. Salamanca: Universidad Pontificia de Salamanca.

Ortiz, G., Quintero, S., & Díaz, A. (2015). Modelo de mediaciones pedagógicas y tecnológicas para incorporar adecuadamente procesos pedagógicos-comunicativos-tecnologicos de ambientes virtuales de aprendizaje en la policia naciona de Colombia. Revista Logos Ciencia & Tecnología, 6(2), 188-197.

Parra, O., & Dìaz, V. (2014). Didáctica de las matemáticas y tecnologías de la información y la comunicación. Educación y Desarrollo Social, 8(2), 60-81. doi:10.18359/reds.295

Ramos, A. I., Herrera, J. A., & Ramírez, M. S. (2010). Developing Cognitive Skills with Mobile Learning: a Case Study. Revista Comunicar, XVII(34), 201-209. doi:10.3916/C34-2010-03-20

Ramos, A. J., Herrera, J. A., & Ramírez, M. S. (2010). Desarrollo de habilidades cognitivas con aprendizaje móvil: un estudio de casos. Revista Comunicar, XVII(34), 201-209. doi:10.3916/C34-2010-03-20

Rincón , O., Vergel, M., & Ortega, S. (2015). El Blog como estrategia Didáctica Innovadora en el Aprendizaje del Cálculo. El Cálculo y su Enseñanza, 6(6), 45-70.

Rincón Leal, O. L. (2016). Tic en la Enseñanza de las Ecuaciones Diferenciales de Primer Orden. Revista Logos Ciencia & Tecnología, 8(1), 89-100. doi:10.22335/rlct.v8i1.347

Rincón Leal, O., & Vergel Ortega, M. (2015). Blogs, su influencia en la enseñanza del Cálculo Integral. En Varios, Educación Internacional Lengua y Cultura. Cali: Redipe.

Ruiz, E. (2014). La tecnología en el aula de clase: De las calculadoras graficadoras a los ambientes virtuales de aprendizaje. Lat Am J. Phys Educ, 8(2), 345-354.

Sabogal, G., Monroy, N., Landero, J. L., & Molina, Y. R. (2015). Cálculo diferencial: aprendiendo con nuevas tecnologías. Revista de Tecnología, 12(2), 42-51.

Sepulveda, P., Trejos, P., Arango, E., Bustos, A., & Arias, A. (2013). Percepciones de los estudiantes universitarios frente al aprendizaje por medio de dispositivos móviles. Revista Educación y desarrollo social, 7(2), 152-165.

Urry, J. (2004). The Complexities of the Global. Lancaster: Published by the Department of Sociology, Lancaster University. Obtenido de http://www.comp.lancs.ac.uk/sociology/papers/urry-complexitiesglobal.pdf

Vargas, L., Gómez, M., & Gómez, R. (2013). Desarrollo de habilidades cognitivas y tecnológicas con aprendizaje móvil. Revista de Investigación Educativa, 3(6).

Vázquez. (2014). Mobile Distance Learning with Smartphones and Apps in Higher Education. Educational Sciences: Theory & Practice, 14(4), 1505-1520.

Vergel, M., Martinez, J., & Zafra, S. (2015). APPS en el rendimiento académico y auto concepto de estudiantes de ingeniería. Logos Ciencia & Tecnología, 6(2), 198-208.

Vergel, M., Rincón, O., & Martínez, J. (2016). Validez de instrumento CALA para evaluar asesorías académicas virtuales. Revista Horizontes Pedagógicos, 18(1), 26-33.

1. Departamento de Matemáticas y Estadística. Universidad Francisco de Paula Santander. Licenciada en Matemáticas y Física, Magister en Educación Matemática. olgarincon@ufps.edu.co

2. Departamento de Matemáticas y Estadística. Universidad Francisco de Paula Santander. Licenciada en Matemáticas y Física, Magister en Educación, Doctora en Educación. mawency@ufps.edu.co

3. Departamento de Matemáticas . Escuela Superior de Administración Pública. Licenciado en  Biología y Química, Magister en Educación, Doctor en Educación.  checo.jf@gmail.com