ISSN 0798 1015

Vol. 39 (Nº 33) Año 2018 • Pág. 10

Evaluación de eficiencia y productividad de PyMEs productivas usando análisis envolvente de datos e índice Malmquist

Evaluation of efficiency and productivity of productive SMEs using data envelopment analysis and Malmquist index

Víctor Hipólito PUMISACHO Álvaro 1; Karla María ALVARADO Ramírez 2

Recibido: 12/03/2018 • Aprobado: 12/04/2018

Contenido

1. Introducción

2. Metodología

3. Resultados

4. Conclusiones

Referencias bibliográficas

1. Introducción

En un ambiente competitivo de negocios, las organizaciones deben recurrir a métodos y técnicas que les permita mejorar su desempeño en lo que respecta a productividad, calidad y eficiencia para alcanzar sus objetivos organizacionales y poder competir (Hayes & Pisano, 1994).  Una forma de controlar si se está avanzando hacia la dirección establecida en su estrategia es realizar mediciones continuas de sus resultados operacionales, con métodos que amplíen el espectro común de los indicadores financieros (Kaplan & Norton, 2002; Díaz-Garrido, Martín-Peña & Sánchez-López, 2011).

La evaluación del desempeño centrada en los logros sostenidos sin tener en cuenta los esfuerzos o recursos comprometidos generalmente menoscaba el verdadero estado competitivo de la organización. Por lo tanto, es necesario desarrollar una medida de desempeño que incluya simultáneamente todos los aspectos de logro considerados como pertinentes para el éxito, y los esfuerzos correspondientes para alcanzarlos (Leachman, Pegels & Shin, 2005). Según Cooper, Seiford & Zhu (2011) debe usarse enfoques nuevos "orientado a los datos" para evaluar el rendimiento de un conjunto de entidades pares denominadas unidades de toma de decisiones (Decision Making Unit - DMU) que convierten múltiples entradas en múltiples salidas.

Esta necesidad de desarrollar mejores métodos y modelos para evaluar el desempeño de DMUs ha sido la motivación de varios autores, iniciando con Farrell en 1957, quienes plantean que una manera de resolver el problema es realizar mediciones claves, para lo cual se necesita un enfoque que permita a la unidad productiva enfocarse en un pequeño número de medidas que tengan en cuenta múltiples aspectos de desempeño (Jain, Triantis & Liu, 2011). En este conjunto de medidas se incluye a la eficiencia en el uso de recursos para obtener productos o servicios con valor y la productividad (Cooper et al., 2011).

La productividad de una entidad organizacional productiva se puede concebir como la relación entre su producción y el o los factores que hicieron esto posible. En el caso de que la DMU utilice varias entradas para producir varias salidas, las salidas en el numerador deben agregarse de alguna manera razonable, al igual que las entradas en el denominador, de modo que la productividad siga siendo la razón de dos escalares (Coelli, Rao, O'Donnell & Battese, 2005). En consecuencia, el crecimiento de la productividad se resume como la diferencia entre el crecimiento del producto y el crecimiento de insumos (Fried, Lovell & Schmidt, 2008).

Banker, Charnes & Cooper (1984) al igual que Charnes, Cooper & Rhodes (1978) plantean que el desempeño de una DMU se puede expresar numéricamente a través de la evaluación comparativa con los competidores de mejor rendimiento. Es así que formulan a la eficiencia como la comparación entre los valores alcanzados y los valores óptimos. Este análisis puede involucrar la comparación de la salida observada con el máximo potencial de salida, obtenido a partir de una entrada establecida; o, la comparación de la entrada observada con la mínima entrada potencial requerida para producir la salida. En otras palabras, el análisis de eficiencia se centra principalmente en la medición de la aptitud con la que las entradas se convierten en salidas con valor, considerando a la organización como una caja negra sin revelar por qué exhibe un nivel particular de eficiencia (Fried et al., 2008). Sengupta, Venkatesh, & Sinha (2013) al igual que Cook, Tone & Zhu (2014), resaltan la necesidad de una medida de eficiencia relativa para la evaluación de DMUs que producen diferentes y múltiples productos utilizando diferentes y múltiples entradas. Eliminar o mejorar las operaciones ineficientes disminuye el costo y aumenta la productividad. La evaluación del desempeño y la evaluación comparativa ayudan a que las DMUs sean más productivas y eficientes (Zhu, 2014).

En la actualidad, las pymes juegan un papel importante en la economía de los países, contribuyendo con la provisión de empleo productivo, la movilización de recursos económicos y la estabilidad socioeconómica. Establecen la vanguardia del sector empresarial moderno y presentan la fuerza más prominente de modernización y crecimiento en las economías en desarrollo (Heilbrunn, Rozenes & Vitner, 2011). En el Ecuador, un país en desarrollo, la contribución de las pymes es significativa. Según los datos disponibles en la Superintendencia de compañías y valores (Supercias), hasta el 30 de junio de 2016, las pymes representan el 41,7% de las empresas del país, contribuyen con el 26% al producto interno bruto ecuatoriano, generan el 31% del empleo y, su aporte de generación de ingresos por ventas constituye el 39%. Sin, embargo, es una característica común en las pymes ecuatorianas, la limitación en recursos y la presencia de dificultades operacionales y de gestión. Ante esta realidad, las pymes solo podrán alcanzar éxito y liderar sus sectores, si usan sus recursos limitados de manera efectiva y orientan sus fortalezas competitivas de manera innovativa (Brophey & Brown, 2009). En este sentido se busca obtener información sobre qué empresas y sus sectores han alcanzado un nivel satisfactorio en el rendimiento empresarial (Bulak & Turkilmaz, 2014). De acuerdo a Zhu (2014) a través de la evaluación del desempeño se puede (i) revelar las fortalezas y debilidades de las operaciones comerciales, actividades y procesos, (ii) preparar mejor al negocio para satisfacer las necesidades y requerimientos de sus clientes; y, (iii) identificar oportunidades para mejorar las operaciones y procesos actuales, y crear nuevos productos, servicios y procesos.

En este contexto, el presente estudio tiene dos objetivos: (i) analizar a 164 pymes, localizadas en el Distrito Metropolitano de Quito, agrupadas en siete sectores productivos a través de su puntuación de eficiencia; y, (ii) determinar los patrones de cambio en la eficiencia de la pymes y sus sectores, durante el período 2010-2015. Para cumplir con este cometido, se utilizó el método de análisis envolvente de datos (Data Envolepment Analysis - DEA) orientado a las entradas, considerando rendimiento de escala variable. Adicional a la evaluación de la eficiencia de este segmento de las pymes ecuatorianas durante seis años, esta investigación muestra cómo las pymes pueden alcanzar una mejor eficiencia con una orientación adecuada en el uso de sus recursos, para esto se compara los puntajes de eficiencia de cada sector y se expone las acciones de mejoras necesarias para convertirse en un sector eficiente.

1.1. Análisis envolvente de datos

El análisis envolvente de datos, o simplemente DEA, es una técnica de programación lineal muy utilizada en la actualidad para medir la eficiencia de diferentes tipos de organizaciones (DMUs) o parte de estas. Está basado en los conceptos de medición de eficiencia productiva propuestos por Farrell (1957) y fue introducida por Charnes et al. (1978) como el modelo CCR. Este primer modelo DEA estaba fundamentado en la suposición de rendimientos de escala constante (Constant Return to Scale - CRS); posteriormente Banker et al. (1984) mejoraron el modelo CCR y desarrollaron el modelo BCC utilizando el concepto de rendimiento de escala variable (Variable Return to Scale - VRS).

El DEA es de naturaleza no paramétrica, que no requiere parámetros predefinidos y unidades uniformes. Puede proporcionar un índice que incorpora varias medidas con buena estabilidad y sensibilidad, siendo muy útil para evaluar la eficiencia relativa de un conjunto homogéneo de DMUs, las cuales de manera análoga producen una variedad de salidas (outputs) con el uso de múltiples entradas (inputs). Muestra además el índice de producción excesivo o insuficiente para las unidades de baja eficiencia (Liao et al., 2016). En otras palabras, la aplicación de esta forma de análisis proporciona una puntuación de eficiencia para cada unidad lo cual permite una comparación entre ellas, además de proveer una orientación de hacia dónde encauzar las acciones para mejorar su eficiencia y alcanzar la frontera eficiente (Kutvonen, 2007).

El objetivo fundamental que persigue esta técnica es determinar si una DMU es eficiente o no; es decir, de un grupo de unidades comparables, cuál o cuáles unidades conforman la llamada frontera de eficiencia y cuáles no la alcanzan (Gok & Sezen, 2011). Por lo tanto, la función objetivo de este modelo es maximizar bajo ciertas condiciones el valor de la proporción salidas sobre entradas ponderadas de un conjunto de DMUs. Según Charnes et al. (1978) el modelo matemático correspondiente para llegar a esta maximización es:

Adicionalmente, los modelos DEA de acuerdo con su orientación están divididos en dos grupos, uno orientado a las entradas (input oriented) y otro orientado a las salidas (output oriented). De acuerdo a Blackburn, Brennan & Ruggiero (2014), en un modelo input orientado, para que una unidad ineficiente llegue a ser eficiente, las acciones se orientan hacia una reducción proporcional de las entradas manteniendo el nivel actual de salidas; en cambio, en un modelo output orientado las acciones se enfoca, a incrementar las salidas de una unidad ineficiente manteniendo los niveles actuales de entradas.

Según Bulak & Turkyilmaz (2014), el método DEA en los últimos años ha sido reconocido por tener ventajas sobre otras técnicas en la medición de la eficiencia, por lo cual ha sido ampliamente usada en distintos campos que incluyen a hospitales, bancos, aerolíneas, universidades, servicios públicos, hoteles, transporte, telecomunicaciones, entre otros.

1.2. Índice de productividad Malmquist

En el análisis de la productividad de una DMU, se identifican dos orientaciones: el de la productividad parcial (Partial Productivity - PP) y el de la productividad total de los factores (Total Factor Productivity - TFP). En la perspectiva PP se compara los cambios en el producto total asociados a cambios de factores productivos específicos individuales, como el capital o el trabajo, mientras que en el enfoque de la TFP se evalúa los cambios en la producción total con los cambios en todos los factores productivos. Conceptualmente la TFP se define como el cociente entre una función que agrega las salidas y una función que agrega las entradas de los procesos productivos, y en forma práctica mide las mejoras de eficiencia en los procesos productivos y el progreso tecnológico (Diewert & Nakamura, 2005).

Actualmente, el enfoque más común para medir la evolución del desempeño de organizaciones, si se dispone de un panel de datos, es aplicar el índice Malmquist al cambio en la productividad total de factores (TFP), esto involucra la medición de cambios tanto en el nivel de salidas producidas como en el nivel de entradas usadas (Jacobs, Smith & Street, 2006).

El índice de productividad Malmquist (Malmquist Productivity Index - MPI) fue desarrollado por Caves, Christensen & Diewert (1982), fundamentados en los números índices propuestos por Malmquist (1953). El MPI se puede obtener a través de diferentes técnicas. La técnica utilizada en este estudio corresponde al uso de fronteras no paramétricas determinísticas aplicando el modelo de análisis de la actividad propuesto por Färe, Grosskopf, Norris & Zhang (1994a), quienes plantean el cálculo del MPI basándose en el en el hecho de que la función de distancia de inputs o de outputs es idéntica al inverso de la medida de eficiencia técnica de Farrell (1957) de inputs o de outputs, respectivamente. Según Marques & Silva (2006), la función distancia de inputs consiste en la reducción máxima proporcional (radial) del vector de inputs, dado un nivel de outputs predeterminado. El MPI se establece como el cociente entre funciones de distancia de fechas distintas, es decir,

La medida de los puntajes de eficiencia técnica debe estar entre 0 y 1. Por lo tanto, un valor de cambio de eficiencia técnica mayor que 1 refleja el movimiento de una unidad particular ineficiente hacia la frontera de rendimientos a escala constante, y se interpreta como una mejora de la eficiencia. En contraste, un valor de este índice menor que 1 se interpreta como el deterioro de la eficiencia. Del mismo modo, un valor de cambio técnico mayor que 1 significa progreso tecnológico o una expansión de la frontera y un valor menor que 1 representa el retroceso tecnológico o la contracción de la frontera. Finalmente, si una DMU entre los períodos t y t+1 tiene un cambio positivo de productividad, entonces el índice tfpch será mayor que 1, si ocurre un cambio negativo será menor que 1 y si no existe ningún cambio, el resultado será igual a 1 (Thayaparan & Pratheepan, 2014).

Para hallar el valor del índice MPI se debe calcular las cuatro funciones de distancia involucradas en su definición, lo que implica resolver al menos cuatro problemas de programación lineal, esto se ve facilitado con el uso de un software apropiado (Lovell, 1996).

El objeto de estudio en la presente investigación fue las pymes de sectores productivos localizadas en el Distrito Metropolitano de Quito, sectorizadas de acuerdo con la Cámara de la Pequeña y Mediana Empresa de Pichincha (CAPEIPI) en siete sectores: Alimenticio, Construcción, Gráfico, Maderero, Metalmecánico, Químico y Textil.

Los criterios para clasificar a una empresa como pyme varían en diversos países, pero por lo general, su clasificación depende del análisis de sus ingresos totales anuales y su número de colaboradores. De acuerdo con la Supercias del Ecuador, se define como pequeña empresa a las compañías que tienen menos de 50 empleados, un valor bruto de las ventas anuales entre 100.001 y 1.000.000 dólares y montos activos de 100.001 hasta 750.000 dólares; y como mediana empresa a las compañías que tienen entre 50 y 199 empleados, un valor bruto de las ventas anuales entre 100.000.001 y 5.000.000 dólares y montos activos de 750.001 hasta 3.999.999 dólares.

Para realizar la evaluación de la eficiencia de las pymes, se utilizó un panel de datos obtenido de los Balances y Estados de situación financiera del Portal de Documentos de la Supercias del Ecuador para el período 2010-2015, considerando de manera rigurosa la completitud de datos de las DMUs para todos los períodos; de tal forma que sean homogéneas y comparables todas las unidades de la muestra, habilitando un análisis estadístico adecuado y la declaración de conclusiones confiables (Kothari, 2004).

2.1. Participantes

El número de pymes pertenecientes a sectores productivos, de acuerdo con la base de datos de la CAPEIPI es de 210 empresas, el mismo que se redujo luego de la evaluación de localización y completitud de datos necesarios en la investigación. Finalmente, el estudio incluyó a 164 pymes ubicadas en el Distrito Metropolitano de Quito distribuidas en siete sectores productivos de la siguiente forma: Alimenticio (16), Construcción (41), Gráfico (18), Maderero (32), Metalmecánico (20), Químico (21) y Textil (16).

El número de pymes en cada sector productivo con los datos completos para todos los años, cumplen con el criterio sugerido por Cooper, Seifor Tone (2007):

# DMUs ≥ max {m × s, 3(m + s)} (4)

donde m es el número de inputs y s es el número de outputs en el análisis.

2.2. Recolección de datos

Las variables necesarias para el cálculo de la eficiencia relativa de las DMUs se dividen en variables de entrada (inputs) y variables de salida (outputs). La eficiencia relativa de cada DMU se define como la razón entre la suma ponderada de sus productos (outputs) y la suma ponderada de los insumos necesarios para generarlos (inputs) (Senra, L., Nanci, L., Soares de Mello, J., & Angulo-Meza, L., 2007).

Los modelos no-paramétricos como el DEA requieren una identificación y medición apropiada de los inputs y outputs a ser usados en la evaluación. Las variables seleccionadas en este estudio están acorde a la literatura y a la información disponible en la base de datos del portal de la Supercias. La Tabla 1 describe los inputs y outputs escogidos para el análisis. Las variables de entrada establecidas son (i) activos fijos, (ii) gastos operacionales y (iii) gastos de personal. La variable de salida determinada es el ingreso por ventas. Los inputs seleccionados son considerados como factores clave para la actividad productiva en una pyme (Bulak & Turkyilmaz, 2014).

Tabla 1
Inputs y Outputs calificados para el análisis de eficiencia

Fuente: Elaborado por los autores

2.3. Análisis de datos

Para cada DMU (pyme) agrupada en los siete sectores productivos se compiló anualmente el valor de cada variable, desde el 2010 al 2015. En la Tabla 2 se presenta los valores promedio anuales determinados para las variables input y output en los siete sectores productivos.

Tabla 2
Valores promedio anuales de las variables input y output.

Fuente: Elaborado por los autores

Con todos los datos recopilados se realizó la evaluación de la eficiencia y productividad a través del programa para análisis envolvente de datos DEAP V2.1. En el análisis se consideró el modelo DEA orientado a entradas, con enfoque de rendimiento a escala variable (VRS). En la orientación VRS, cualquier unidad k se compara con el 100% de unidades técnico-eficientes (Gok & Sezen, 2011). Las estadísticas descriptivas y gráficas fueron elaboradas usando el programa OriginPro 2017.

3.1. Análisis de eficiencia

La información proporcionada por el DEAP respecto a la eficiencia anual de las DMUs, analizadas por sector productivo, fueron recogidas en un gráfico tipo Box + Data Overlap, style Diamond Box, donde se puede observar la dispersión de los valores de eficiencia alcanzadas por las DMUs del sector respectivo en cada año, así mismo se presenta los valores promedio por año y el valor promedio para todo el período de estudio. Adicionalmente se muestra el número de DMUs que conformaron la frontera de eficiencia con un puntaje de 1 en cada año y el número promedio de DMUs eficientes durante los seis años analizados. En la Figura 1 se exhibe la evaluación de eficiencia para los siete sectores productivos.

Figura 1
Panel de evaluación de eficiencia por sector productivo.

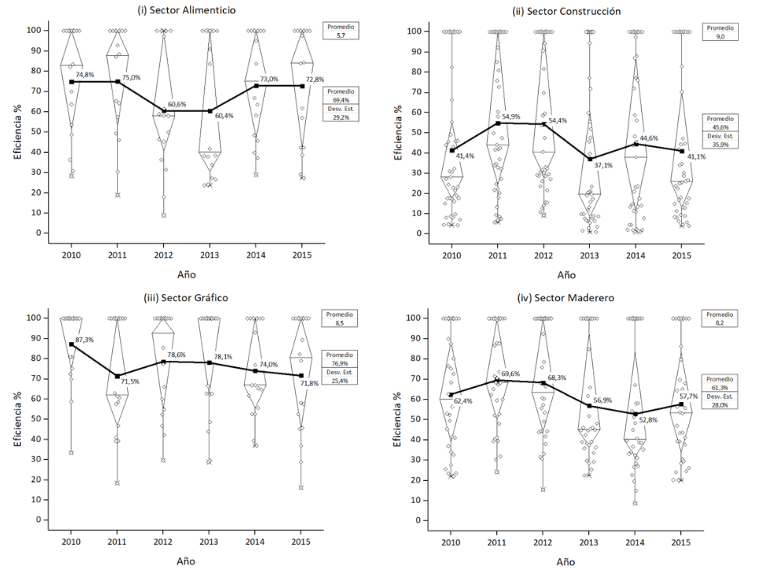
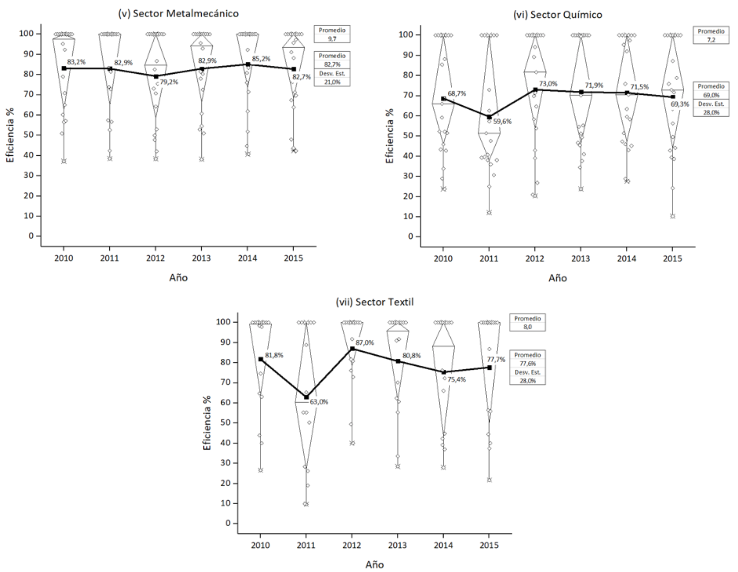
Elaborado por los autores

Según los resultados de la evaluación durante el período de estudio, de los siete sectores en análisis, el sector Metalmecánico tiene el puntaje de eficiencia promedio más alto (82.7%), seguido del sector Textil con 77.6%; por el contrario, el sector de la Construcción presenta el puntaje de eficiencia promedio más bajo (45.6%). Igualmente se observa que el sector Metalmecánico presenta una mayor estabilidad en la eficiencia durante los seis años, con una desviación estándar de la media anual del 21.0%. Otro sector estable es el Gráfico con una desviación estándar de la media anual del 25.4%. En cambio, el sector de la Construcción exhibe una alta variabilidad en la eficiencia, representada por una desviación estándar de la media anual del 35.9%.

Analizando el número de DMUs eficientes, se observa que el sector Textil y el sector Metalmecánico presentan las mejores relaciones del número promedio anual con respecto al número total de DMUs que conforman el sector, 8.0 de 16 (50.0%) y 9.7 de 20 (48.5%) respectivamente. En contraste, el sector de la Construcción exhibe la peor relación, 9.0 de 41 (21.9%).

En resumen, la evaluación de la eficiencia anual por sectores evidencia la mejor situación de los sectores Metalmecánico y Textil, y la peor situación del sector de la Construcción con respecto a los otros sectores.

3.2. Análisis de holguras

Según Novaes, Silveira & Medeiros (2010) la ineficiencia de una DMU es medida por la distancia desde el punto que representa sus valores de entrada y salida observados al punto de referencia correspondiente en la frontera de producción, por tanto, se puede decir que está causado por el uso no adecuado de entradas y/o salidas.

El análisis de holguras (slacks) de las variables en el análisis envolvente de datos (DEA), revela la dirección a seguir para reducir la ineficiencia de las DMUs a través de un mejor uso de los inputs o aumentando los outputs generados. Por tanto, un valor input slack representa las reducciones necesarias de los correspondientes inputs para convertir una DMU en eficiente. De igual forma, un valor output slack representa el nivel adicional de outputs necesarios para convertir una DMU ineficiente en una DMU eficiente (Coelli, 1996).

Las holguras de las variables de entrada: activos, gastos y salarios; y, de la variable de salida: ingresos, aplicadas en este estudio, obtenidas en la evaluación han sido resumidas y se presentan en la Tabla 3.

Tabla 3
Holguras promedio de las variables de entrada y de salida, por sector productivo.

Fuente: Elaborado por los autores

Los valores de holgura muestran que, en los inputs, los activos en todos los sectores deben disminuir, pero en mayor proporción en los sectores de la Construcción y Maderero. Igualmente, los gastos deben reducirse en todos los sectores, pero con mayor énfasis en los sectores Alimenticio y Químico. También los salarios deben contraerse principalmente en el sector de la Construcción. En el lado del output, los sectores que mayor holgura presentan son el de la Construcción y el Textil, y solo el sector Químico muestra una holgura mínima, por lo que puede ser considerado como el modelo a seguir.

La evaluación de holguras orienta las acciones a seguir para el mejoramiento de la eficiencia en todos los sectores. De acuerdo con los hallazgos presentados, el sector de la Construcción es el que presenta una situación más difícil, en su planificación de actividades de mejora deberá considerar reducir las holguras tanto en las entradas como en la salida. Por el contrario, los otros sectores deberán poner énfasis en la planificación de acciones de mejora principalmente en las entradas.

3.3. Análisis del cambio en los niveles de eficiencia durante el período 2010-2015

Para analizar el cambio en la eficiencia de una DMU entre dos o más períodos de tiempo resulta útil el uso del índice de Malmquist (MPI) y sus componentes definidos como: el índice de productividad total de los factores (tfpch), que mide la eficiencia económica o total; el índice de eficiencia (effch), que mide la capacidad de utilizar los inputs en proporciones óptimas dados sus precios respectivos, de tal forma que sólo existe una combinación de inputs que minimiza el coste de una producción determinada, es conocido también como eficiencia asignativa; y, el índice de productividad del cambio técnico (techch), que refleja la eficiencia técnica; es decir, la capacidad de obtener el máximo producto dado un conjunto de factores tecnológicos (Fried et al., 2008). Con el objetivo de analizar el desempeño de los siete sectores productivos en el período 2010-2015 se procedió a evaluar el cambio de eficiencia de estos sectores en los períodos 2010-2011, 2011-2012, 2012-2013, 2013-2014, 2014-2015, resultados que se exhiben en la Figura 2 a través de gráficas de tipo Double Y Graph, donde se muestra la evolución de la productividad total de factores (tfpch) medida con la escala vertical izquierda; y, los cambios de la eficiencia técnica (effch) y tecnología (techch) medidas a través de la escala vertical derecha.

Figura 2
Panel de la evolución de cambio de productividad, eficiencia y tecnología por sector productivo. Elaborado por los autores.

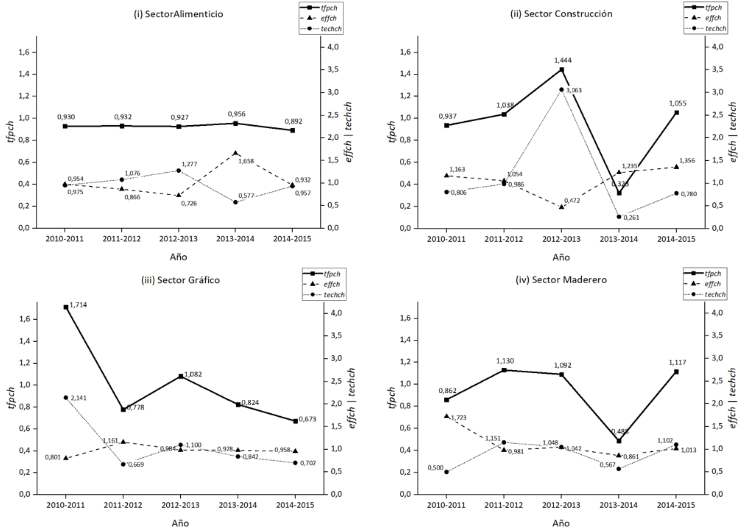
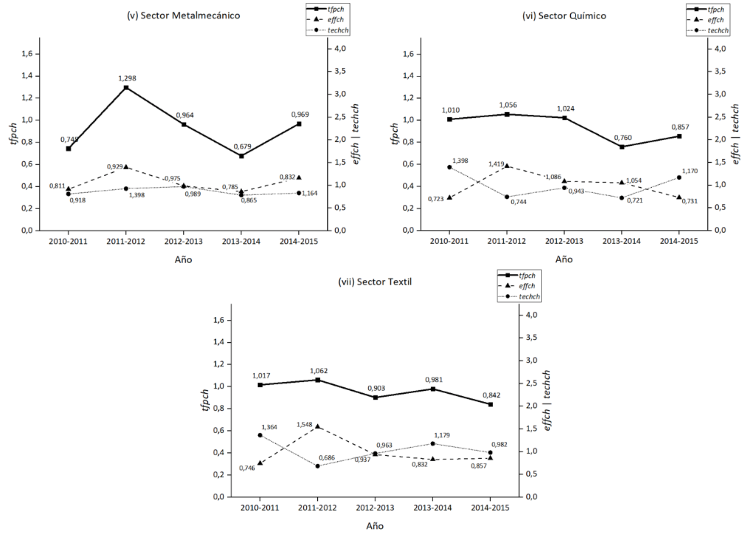
Los resultados de cambio de productividad, eficiencia técnica y eficiencia tecnológica, durante el período 2010-2015, muestran que el comportamiento de los siete sectores es muy variable. Así, el sector Alimenticio evidencia que disminuyó la productividad todos los años analizados, en cambio los otros sectores de un año a otro exhiben un aumento en la productividad por lo menos una vez, siendo los sectores de Construcción, Maderero y Químico los que lograron mejorar su productividad durante tres transiciones anuales. También se puede observar en este panel de resultados que no existe predominio del cambio de eficiencia técnica ni del cambio de eficiencia tecnológica en el comportamiento de la productividad total de los factores.

De acuerdo con la definición del índice de Malmquist, si de un período a otro el valor obtenido por una DMU es mayor que 1, ha existido un incremento en su productividad, en caso contrario si es menor que 1 ha existido una disminución en su productividad (Färe, Grosskopf, Lindgren & Roos, 1994b). En la Tabla 4, se presenta una evaluación de la productividad total por períodos de dos años, resumiendo el número de DMUs cuyo índice MPI fue mayor que 1, igual a 1 o menor que 1; es decir, que tuvieron un cambio positivo, no tuvieron cambio o tuvieron un cambio negativo respectivamente.

Tabla 4
Tabulación de DMUs de acuerdo con el cambio en su productividad.

Fuente: Elaborado por los autores.

De acuerdo con la medición de la evolución de la productividad de los sectores, a través del índice de Malmquist, el sector Alimenticio a pesar de tener un promedio de productividad total de los factores (tfpch) menor que la unidad en todos los años, al igual que el sector Químico, muestran un comportamiento más estable en el número de DMUs que tuvieron un cambio positivo. En contraste, los sectores de la Construcción, Maderero y Metalmecánico presentan una evolución más variable en el número de DMUs que mejoraron su productividad de un año a otro. La situación de los sectores Gráfico y Textil es preocupante, debido a que, en el período de estudio, el número de DMUs que han tenido un cambio positivo ha ido decreciendo año tras año. En general, se puede observar que en todos los sectores y en todos los años, el número de DMUs que tuvieron un cambio positivo es similar al número de DMUs que tuvieron un cambio negativo, es decir, redujeron su productividad.

En el presente trabajo se presenta los resultados de la medición de eficiencia y el cambio de productividad total de los factores (TFP) de pymes ecuatorianas pertenecientes a siete sectores de manufactura, en el período 2010-2015. La evaluación de la eficiencia de las pymes se realizó a través de un modelo DEA de rendimientos variables a escala (VRS) con orientación input; y, la evolución de la productividad de las pymes y sus sectores se analizó usando el Índice de Productividad de Malmquist (MPI), el mismo que exhibe, además del cambio de la productividad total de los factores (ftpch), el cambio en sus dos componentes: eficiencia técnica (effch) y cambio tecnológico (techch).

Los modelos no-paramétricos como el DEA requieren una identificación y medición apropiada de los inputs y outputs a ser usados en la evaluación. Una debilidad conocida del DEA es su baja capacidad de ordenar las DMUs, ya que cuanto mayor es el número de variables con relación al número de DMU, menor será la capacidad de ordenación por las eficiencias, debido a la tendencia de varias DMUs de quedarse en la frontera de máxima eficiencia. Una de las maneras de evitar este problema es restringir el número de variables utilizadas en el análisis. En este estudio fueron establecidas las variables acorde a la literatura y a la información disponible, fijándose como variables de entrada a: (i) activos fijos, (ii) gastos operacionales y (iii) gastos de personal; y, como variable de salida al ingreso por ventas.

De acuerdo con los resultados obtenidos durante el período 2010-2015 sobre la eficiencia, se observa la presencia de una evaluación de eficiencia marcadamente baja para el sector de la Construcción lo que le sitúa como el sector menos eficiente de todos los siete sectores. Así mismo se observa que ningún sector presenta un puntaje alto de eficiencia, lo que refleja el desempeño de las DMUs que conforman cada sector, por tanto, el campo para implementar acciones de mejora es bastante amplio. Sin embargo, los propietarios o responsables de cada pyme deberán entender los principios básicos de la eficiencia y la productividad y deberán enfocar las actividades de mejora a reducir las brechas en las variables críticas sean estas de entrada o de salida.

Los resultados de cambio de productividad, eficiencia técnica y eficiencia tecnológica, durante el período en estudio, muestran que el comportamiento de los siete sectores es muy variable. Rescatando a los sectores de Construcción, Maderero y Químico como aquellos que lograron mejorar su productividad durante tres transiciones anuales. También se pudo evidenciar que no existe predominio del cambio de eficiencia técnica ni del cambio de eficiencia tecnológica en el comportamiento inestable de la productividad total de los factores.

Del análisis de la evolución de productividad se puede resaltar además que, a pesar de las dificultades de alcanzar eficiencia, en el sector Alimenticio y Químico el número de DMUs que muestran un cambio positivo se mantiene estable. El resto de los sectores muestran que el número de DMUs que evolucionaron positivamente ha ido disminuyendo o presentan un comportamiento variable.

Una limitación del estudio es que muchas de las pymes no declaran todos los años sus estados de resultados y balances de situación, lo que impide construir paneles completos y balanceados. Además, que los ítems de información requerida en estos informes han cambiado desde el año 2012, lo que dificulta disponer de información homogénea durante todo el periodo en estudio.

Banker, R., Charnes, A., & Cooper, W. (1984). Some models for estimating technical and scale in-efficiencies in data envelopment analysis. Management Science, 30(9), 1078-1092. https://doi.org/10.1287/mnsc.30.9.1078.

Blackburn, V., Brennan, S., & Ruggiero, J. (2014). Nonparametric Estimation of Educational Production and Costs using Data Envelopment Analysis. New York: Springer US.

Brophey, G., & Brown, S. (2009). Innovation practices within small to medium-sized mechanically based manufacturers. Innovation: Management, Policy & Practice, 11(3), 327-340. https://doi.org/10.5172/impp.11.3.327.

Bulak, M., & Turkyilmaz, A. (2014). Performance assessment of manufacturing SMEs, a frontier approach. Industrial Management & Data Systems, 114(5), 797-816. https://doi.org/10.1108/IMDS-11-2013-0475.

Caves, D., Christensen, L., & Diewert, W. (1982). The economic theory of index numbers and the measurement of input, output, and productivity. Econometrica, 50(6), 1393-1414. doi: 10.2307/1913388.

Charnes, A., Cooper, W., & Rhodes, E. (1978). Measuring the efficiency of decision making units. European Journal of Operational Research, 2(6), 429-444. https://doi.org/10.1016/0377-2217(78)90138-8.

Coelli, T. (1996). A Guide to DEAP Version 2.1: A Data Envelopment Analysis (Computer) Program. CEPA Working Paper, 1-49.

Coelli, T., Rao, D., O'Donnell, C., & Battese, G. (2005). An introduction to efficiency and productivity analysis. New York: Springer.

Cook, W. D., Tone, K., & Zhu, J. (2014). Data envelopment analysis: Prior to choosing a model.

OMEGA, 44(C), 1-4. http://dx.doi.org/10.1016/j.omega.2013.09.004.

Cooper, W., Seifor, L., & Tone, K. (2007). Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software. New York: Springer-Verlag.

Cooper, W., Seiford, L., & Zhu, J. (2011). Data envelopment analysis: History, models, and interpretations. In Handbook on Data Envelopment Analysis (pp, 1-39). Boston: Springer. DOI 10.1007/978-1-4419-6151-8_1.

Díaz-Garrido, E., Martín-Peña, M.L. & Sánchez-López, J.M. (2011). Competitive priorities in operations: Development of an indicator of strategic position. CIRP Journal of Manufacturing Science and Technology, 4(1), 118-125.   DOI:10.1016/j.cirpj.2011.02.004.

Diewert, W., & Nakamura, A. (2005). Concepts and Measures of Productivity: An Introduction. In Services Industries and the Knowledge Based Economy. Calgary: University of Calgary Press.

Färe, R., Grosskopf, Sh., Norris, M., & Zhang, Zh. (1994a). Productivity Growth, Technical Progress, and Efficiency Change in Industrialized Countries. The American Economic Review, 84(1), 66-83.

Färe, R., Grosskopf, Sh., Lindgren, B., & Roos, P. (1994b). Productivity Developments in Swedish Hospitals: A Malmquist Output Index Approach. In Data Envelopment Analysis: Theory, Methodology, and Applications (253-272). New York: Springer. DOI: 10.1007/978-94-011-0637-5.

Farrell, M. (1957). The Measurement of Productive Efficiency. Journal of the Royal Statistical Society Series A (General), 120(3), 253-290. http://dx.doi.org/10.2307/2343100.

Fried, H., Lovell, C., & Schmidt, Sh. (2008). The Measurement of Productive Efficiency and Productivity Growth. New York: Oxford University Press.

Gok, M. S., & Sezen, B. (2011). Analyzing the Efficiencies of Hospitals: An Application of Data Envelopment Analysis. Journal of Global Strategic Management, 5(2), 137-146. DOI: 10.20460/JGSM.2011515804.

Hayes, R., & Pisano, G. (1994). Beyond world-class: the new manufacturing strategy. Harvard Business Review. 72(1), 77-86.

Heilbrunn, S., Rozenes, S. & Vitner, G. (2011). A DEA based taxonomy to map successful SMEs. International Journal of Business and Social Science, 2(2), 232-241.

Jacobs, R., Smith, P., & Street, A. (2006). Measuring Efficiency in Health Care: Analytic Techniques and Health Policy. Cambridge: Cambridge University Press.

Jain, S., Triantis, K.P., & Liu, S. (2011). Manufacturing performance measurement and target setting: a data envelopment analysis approach. European Journal of Operational Research, 214(3), 616-626. doi:10.1016/j.ejor.2011.05.028.

Kaplan, R., & Norton, D. (2002). Cuadro de Mando Integral. Barcelona: Gestión 2000.

Kothari, C. (2004). Research Methodology – Methods & Techniques. New Delhi: New Age International Limited.

Kutvonen, A. (2007). Ranking regional innovation policies: DEA-based benchmarking in a European setting. Research report 193. Lappeenranta, Finland: Lappeenranta University of Technology.

Leachman, Ch., Pegels, C., & Shin, S. (2005). Manufacturing performance, evaluation and determinants. International Journal of Operations & Production Management, 25(9), 851-874. https://doi.org/10.1108/01443570510613938.

Liao, J.-F., Wang, J., Liang, L., Wu, Y.-D., Huang, M.-J., Liu, T.-Q., … Wang, X.-W. (2016). An evaluation study of research efficiency of the Guangzhou institute of respiratory diseases based on malmquist index. Journal of Thoracic Disease, 8(10), 2709–2716. http://doi.org/10.21037/jtd.2016.09.51

Lovell, C. (1996). Applying Efficiency Measurement Techniques to The Measurement of Productivity Change. Journal of Productivity Analysis, 7(2/3), 329-340.

Malmquist, S. (1953). Index Number and Indifference Surfaces. Trabajos de Estadística, 4(2), 209-242. http://dx.doi.org/10.1007/BF03006863

Marques, R., & Silva, D. (2006). Análise da variação da produtividade dos serviços de água Portugueses entre 1994 e 2001 usando a abordagem de Malmquist. Pesquisa Operacional, 26(1),  145-168.  http://dx.doi.org/10.1590/S0101-74382006000100008.

Novaes, A., Silveira, S., & Medeiros, H. (2010). Efficiency and productivity analysis of the interstate bus transportation industry in Brazil. Pesquisa Operacional, 30(2), 465-485. http://dx.doi.org/10.1590/S0101-74382010000200012.

Örkcü, H., Balikçi, C., Dogan, M., & Genç, A. (2016). An evaluation of the operational efficiency of turkish airports using data envelopment analysis and the Malmquist productivity index, 2009-2014 case. Transport Policy, 48(C), 92-104.  DOI:10.1016/j.tranpol.2016.02.008.

Sengupta, A., Venkatesh, D., & Sinha, A. (2013). Developing performance-linked competency model, a tool for competitive advantage. International Journal of Organizational Analysis, 21(4), 504-527. https://doi.org/10.1108/IJOA-05-2011-0488.

Senra, L., Nanci, L., Soares de Mello, J., & Angulo-Meza, L. (2007). Estudo sobre métodos de seleção de variáveis em DEA. Pesquisa Operacional, 27(2), 191-207. http://dx.doi.org/10.1590/S0101-74382007000200001.

Thayaparan, A., & Pratheepan, T. (2014). Evaluating total factor productivity growth of commercial banks in Sri Lanka: An application of Malmquist index. Journal of Management Research, 6(3), 58-68. DOI: 10.5296/jmr.v6i3.5513.

Zhu, J. (2014). Quantitative Models for Performance Evaluation and Benchmarking: Data Envelopment Analysis with Spreadsheets. New York: Springer.

1. Profesor. Departamento de Ciencias Administrativas. Escuela Politécnica Nacional. Magister en Ingeniería Industrial. victor.pumisacho@epn.edu.ec

2. Profesora. Departamento de Ciencias Administrativas. Escuela Politécnica Nacional. Maestra en Administración. karla.alvarado@epn.edu.ec