

Vol. 39 (Nº 16) Año 2018 • Pág. 23
GÓMEZ-MONTOYA, Rodrigo A. 1; CANO, Jose A. 2; CAMPO, Emiro A. 3
Recibido: 20/12/2017 • Aprobado: 21/01/2018
2. Descripción y formulación del problema
4. Planificación del experimento
RESUMEN: En este artículo se modela el slotting de mínimo costo en centros de distribución, considerando múltiples SKU y sistemas de almacenamiento heterogéneos. Para esto, se implementa un método de optimización, un metaheurístico de búsqueda tabú y una regla empírica. Como resultado de un diseño de experimentos, se obtiene que el tamaño de lista de acomodo tiene un efecto significativo sobre el slotting, y que el método de optimización genera una reducción en costos de mano de obra respecto al metaheuristico. |
ABSTRACT: In this article, the minimum slotting cost in distribution centers is modeled, considering multiple SKUs and heterogeneous storage systems. For this, an optimization method, a taboo search metaheuristic and an empirical rule are implemented. As a result of a design of experiments, it is obtained that the slotting list size has a significant effect on the slotting process, and that the optimization method generates a reduction in labor costs compared to the metaheuristic. |
En el ámbito empresarial, las cadenas de suministro están conformadas por proveedores, empresas ancla y clientes, las cuales gestionan flujos de información, productos y dinero, que se generan por procesos logísticos y organizaciones según los modelos de negocio establecidos (Cano, Panizo, García, & Rodríguez, 2015a; Rojas, Guisao, & Cano, 2011). Estos procesos logísticos pueden agruparse principalmente en sistemas de abastecimiento y compras (Rodrigo A Gómez, Cano, & Campo, 2016), sistemas de producción y manufactura (Arango, Cano, & Alvarez, 2012), sistemas de almacenamiento (Rodrigo A Gómez, Giraldo, & Campo, 2016), sistemas de distribución y transporte (Cano, Panizo, García, & Rodríguez, 2015b), y sistemas de devoluciones y flujos inversos (R. Gómez, Zuluaga, & Correa, 2014; Rodrigo Andrés Gómez, 2010).
Los Centros de Distribución (CEDI), y en general los almacenes son un proceso logístico clave en la cadena de suministro, que permiten administrar inventarios, regular la oferta y demanda, así como atender los requerimientos internos y externos de las empresas. Inclusive, el CEDI es un proceso clave en la agilidad de la cadena de suministro, el cumplimiento de los niveles de servicio, entregas OTIF (On Time, In Full), entre otros indicadores claves de desempeño (Cortes et al., 2017).
Un CEDI comúnmente, se conforma por componentes estratégicos, tácticos y operativos. En el componente estratégico y táctico, se considera el plan maestro, la programación e indicadores claves de desempeño. En tanto, el componente operativo está compuesto por operaciones tales como: recepción, acomodo, preparación de pedidos y despacho. Debe resaltarse, que el desempeño de las diferentes operaciones impacta en la eficiencia, capacidad de respuesta y nivel de servicio del CEDI (Bartholdi y Hackman, 2008; Gómez et al., 2016)(Salazar, Gomez, & Cano, 2017).
La asignación de posiciones de almacenamiento (slotting) es una decisión que impacta transversalmente las operaciones de acomodo, almacenamiento y preparación de pedidos. El slotting impacta al acomodo porque este determina en qué posiciones de almacenamiento deben ubicarse los productos, considerando factores como las características de los SKU (Stock Keep Units), el sistema de almacenaje, entre otros. Del mismo modo, el almacenamiento se relaciona con el slotting respecto a la gestión del inventario (físico y documental); y así mismo las decisiones de asignación de posiciones de almacenamiento impactan en la eficiencia y velocidad de la operación de preparación de pedidos (order picking), ya que influye en la ubicación de los productos con más popularidad o rotación en posiciones de almacenamiento de fácil acceso, que permitan reducir los tiempos de recorrido a través de rutas o tours de mínima distancia (Cano, Gomez, & Salazar, 2017).
A partir de una revisión de la literatura, se identifican artículos de slotting enfocados en la implementación de métodos de optimización (Kutzelnigg, 2011; Heragu et al., 2005; Hou et al., 2010; Takahama et al., 2002) y metaheurísticos (Kim y Smith, 2012; Muppanimuppant y Adil, 2008). Una limitante de los artículos revisados es que se modelan decisiones de slotting considerando SKUs y sistemas de almacenamiento con características homogéneas. Por lo tanto, de la revisión de la literatura no se detectan artículos científicos que modelen simultáneamente las especificaciones de los SKU (largo, alto, ancho y peso) y los sistemas de almacenamiento, así como su integración con tecnologías de información y comunicación (TIC) tales como el WMS (Warehouse Management System) que permitan una gestión eficiente de la operación (Correa, Gómez, & Cano, 2010).
Por los motivos expuestos, el presente artículo tiene como objetivo modelar la decisión de slotting de mínimo costo en CEDI considerando SKU y sistemas de almacenamiento con características heterogéneas, e integración con TIC como el WMS que permitan una ejecución efectiva. Para la solución del problema se considera un método de optimización, un metaheurístico de búsqueda tabú, y una regla empírica.
El resto del artículo, se divide en las siguientes secciones. En la segunda sección, se presenta la descripción y formulación del problema de slotting considerando parámetros, función objetivo, restricciones, entre otros. En la tercera sección, se presenta el método de solución cuantitativo que se implementa para el problema considerando SKU y sistemas de almacenamiento heterogéneos, así como la integración con un WMS. En la cuarta sección, se desarrolla un diseño de experimentos estadístico que permite comparar el desempeño del método cuantitativo para el slotting respecto a un método empírico empresarial. En la quinta sección se presentan los resultados del diseño de experimentos, que permiten detectar estadísticamente cuales factores tienen mayor impacto sobre el costo total de la operación. Finalmente, en la sexta sección, se presentan las conclusiones y trabajos futuros que se generan del desarrollo del artículo.
En esta sección, se presenta la descripción y formulación del problema de asignación de posiciones de almacenamiento (slotting) de mínimo costo en un sistema de almacenaje de cajas.
El área de forward pick en un CEDI es modelado para el problema de asignación de posiciones de almacenamiento (slotting). El sistema de almacenamiento se conforma por un conjunto de cuerpos (bay) de estanterías de cajas (carton rack). Cada cuerpo de estantería se compone de varios niveles de altura y de una capacidad de almacenamiento según dimensiones (alto, largo y ancho) y volumen. Los productos almacenados en la zona de reserva (bulk storage area) son abastecidos a los cuerpos de estantería de cajas del área de forward pick según la política de reabastecimiento fijada, la cual es información de entrada en el presente problema.
La asignación de posiciones de almacenamiento considera restricciones asociadas a las estanterías de cajas y los productos a ser almacenados. Debe tenerse en cuenta, que los productos tienen un peso, volumen, dimensiones (largo, ancho y alto), así como condiciones de contaminación cruzada con otros productos. Por este motivo, los productos que se asignan a una posición de almacenamiento deben cumplir con las restricciones físicas del sistema de almacenamiento y con la capacidad de almacenamiento disponible para garantizar una solución factible al problema.
El problema de asignación de posiciones de almacenamiento, consiste en determinar en qué posiciones disponibles de los cuerpos de estantería deben ser ubicados los productos, con el fin de obtener los menores costos de mano obra en el área de forward pick, cumpliendo así con las restricciones establecidas. Debe tenerse en cuenta, que este problema es clasificado en la categoría de modelos de optimización de asignación.
Para la formulación matemática de un modelo lineal que permita hallar minimizar los costos totales que genera el acomodo en un CEDI, se tienen en cuenta los parámetros de la Tabla 1.
Tabla 1
Parámetros para la modelación del acomodo en CEDI
Parámetro |
Descripción |
n |
Cantidad de SKU que se almacenan en el CEDI |
i |
Índice para identificar cada SKU, donde i = (1,2,3,…..n) |
vi |
Fracción de espacio o volumen asignado al SKU i |
pi |
Número pronosticado de recogidas del SKU i para atender los pedidos de los clientes |
c2 |
Costo promedio por recogida desde el área de bulk storage |
cr |
Costo de reabastecimiento de un SKU al área de forward pick desde el área de bulk storage |
ci |
Costo de recoger el SKU i desde el área de forward pick |
vi |
Volumen del SKU i gestionado en el área de forward pick |
fi / vi |
Número de reabastecimientos por año para cada SKUi |
Como variable de decisión se define la variable binaria Xi, la cual toma valores iguales a 1 cuando un SKU es almacenado y recogido desde el área de forward pick, y toma un valor de 0 en otros casos. Para expresar la función objetivo y las restricciones del modelo matemático se expresan a través de la ecuación (1-4).

En esta sección, se presentan las etapas que se implementan para solucionar el problema de slotting. En la Figura 1, se representan las etapas que conforman el enfoque de solución establecido, y que se explican a detalle a continuación.
Figura 1
Etapas de enfoque de solución del problema de slotting
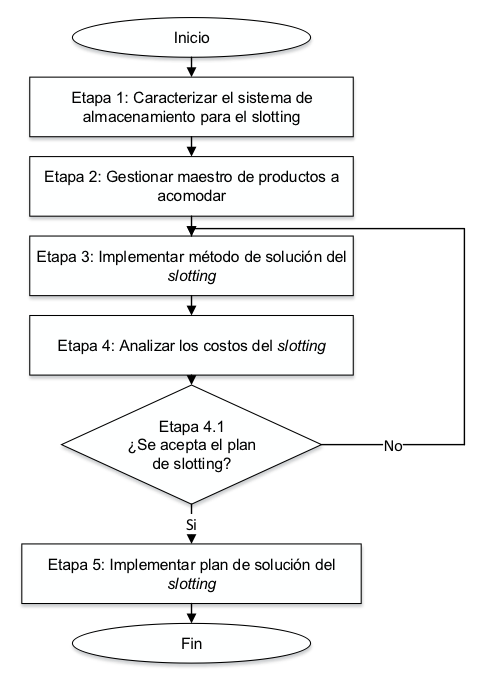
En esta etapa se caracteriza el sistema de almacenaje de cajas, que incluye la cantidad y capacidad de las posiciones almacenamiento (volumen), y sus dimensiones (largo, ancho y alto). Además, se establece la cantidad de cuerpos de estanterías (bays) que la conforman, así como su distribución física en el almacén.
En esta etapa se caracteriza el maestro de productos que deben ser asignados a las posiciones de almacenamiento utilizando el método de slotting. La caracterización del maestro considera información relacionada con dimensiones (largo, ancho y alto del producto), orientación de almacenamiento (hacia arriba o cualquier orientación), volumen, y restricciones de almacenamiento cruzado. Adicionalmente, se establece en qué posiciones de almacenamiento se puede almacenar los SKU i según la clasificación ABC (información que se asume de entrada en el problema).
Se ejecuta uno de los enfoques de solución del problema de slotting. El primer enfoque es un modelo de optimización matemática, que genera la mejor solución posible de slotting. Su limitación es el tamaño del problema, ya que permite modelar máximo 1.000 SKU y 50 cuerpos de estanterías de 4 niveles. El segundo enfoque, es un metaheurístico de búsqueda tabú que genera soluciones seudo-óptimas pero no tiene restricciones en la cantidad de SKU y cuerpos de estanterías en el problema de asignación de almacenamiento. Este enfoque se basa en una estrategia de exploración de vecindarios utilizando memorias del corto plazo durante un número de iteraciones. Finalmente, el tercer enfoque es una regla empírica que consiste en asignar los productos a las posiciones de almacenamiento utilizando la regla (FIFO - First In First Out) y la clasificación ABC de las zonas del almacén, considerando el criterio que hace que los productos de mayor rotación se ubiquen cerca de la zona de consolidación de pedidos y despacho.
En esta etapa se miden y analizan los costos del plan de slotting generados por el método de solución implementado. Los resultados de los costos obtenidos, se comparan con la meta fijada, y se define si se acepta el plan de slotting o se implementa nuevamente el método. Esta etapa, se ejecuta durante un número de iteraciones.
El plan seleccionado, se implementa en el WMS para ejecutar la operación de acomodo en el CEDI. El plan es el informe de salida de la solución del problema de slotting.
En esta sección, se realiza la planeación del experimento que permite evaluar el efecto estadístico de los factores del slotting sobre el costo total que estos generan en el CEDI. Entre los factores que se evalúan se considera la ubicación del depot (punto de inicio y final de la operación de acomodo), método de solución (método de optimización óptima respecto a metaheuristico de búsqueda tabú y regla empírica) y tamaño de lote de productos a acomodar.
Para desarrollar la experimentación, se selecciona un DOE (Design of Experiment) factorial completo 3x2x3, ya que no existen restricciones a la aleatorización con los niveles de los factores modelados para el problema de slotting en el CEDI. La estructura del DOE que se plantea se presenta en la Tabla 2.
Tabla 2
Future research trends for the order picking optimization problem
DOE Factorial Completo 3x2x3 |
Tratamientos |
Replicas |
Corridas |
|||
18 |
4 |
72 |
||||
Variable respuesta |
Costo total de mano de obra en el CEDI debido al slotting |
|||||
Factor |
Niveles |
|||||
1 |
2 |
3 |
|
|||
Método de solución |
Solución óptima
|
Metaheurístico (Búsqueda Tabú) |
Regla empírica |
|||
Depot |
Central |
Left |
|
|||
Tamaño de lote de productos a acomodar |
150 unidades |
250 unidades |
500 Unidades |
|||
Método de optimización |
Se implementa el modelo de optimización utilizado en el software de carton slotting desarrollado por Georgia Tech. El software fue diseñado en JAVA ® y ejecutado Netbeans, IDE 7.0.1, disponible para Windows ® en un computador con procesador Intel Pentium 4 de 3.20GHz y memoria RAM de 1 Gb. |
|||||
Parámetros de la Búsqueda Tabú |
|
|||||
En esta sección, se presentan los resultados obtenidos de la solución del problema de slotting. En la Tabla 3, se presenta el análisis de varianza (ANOVA) que permite identificar cuáles efectos principales e interacciones de los tres factores representados para el problema de slotting tienen un efecto significativo sobre el costo total de mano de obra en la gestión de almacenes (variable de interés).
Tabla 3
ANOVA del problema de slotting
Fuente |
GL |
SC Ajust. |
MC Ajust. |
Valor F |
Valor p |
Modelo |
17 |
5,36E+11 |
3,1521E+10 |
92,28 |
0,000 |
Lineal |
5 |
5,22E+11 |
1,04E+11 |
305,88 |
0,000 |
Método solución |
2 |
6,639E+10 |
3,3195E+10 |
97,18 |
0,000 |
Depot |
1 |
32591033 |
32591033 |
0,1 |
0,759 |
Tamaño de lote |
2 |
4,56E+11 |
2,28E+11 |
667,48 |
0,000 |
Interacciones de 2 términos |
8 |
1,3326E+10 |
1665803220 |
4,88 |
0,000 |
Método solución*Depot |
2 |
77566180 |
38783090 |
0,11 |
0,893 |
Método solución*Tamaño de lote |
4 |
1,3068E+10 |
3267015582 |
9,56 |
0,000 |
Depot*Tamaño |
2 |
180797248 |
90398624 |
0,26 |
0,769 |
Interacciones de 3 términos |
4 |
108209944 |
27052486 |
0,08 |
0,988 |
Método solución*Depot*Tamaño de lote |
4 |
108209944 |
27052486 |
0,08 |
0,988 |
Error |
36 |
1,2297E+10 |
341584777 |
|
|
Total |
53 |
5,48E+11 |
|
|
|
De la ANOVA de la Tabla 3, se detecta que la interacción doble del factor “método de solución” (optimización, metaheurístico y regla empírica) con el factor tamaño de lote de acomodo tiene un efecto significativo sobre el costo total de mano de obra en la gestión de almacenes (variable respuesta), ya que su valor p es menor a 0,05. De otra parte, el factor depot no tiene efecto significativo sobre la variable respuesta de interés, de allí, que sea indiferente ubicarlo en el centro o izquierda del almacén en el problema de slotting.
Para analizar las diferencias entre las combinaciones de los niveles de la interacción doble del enfoque de solución y tamaño de lote de acomodo, a continuación se presenta en la Figura 2 el gráfico de los costos de mano de obra promedio en la gestión de almacenes.
Figura 2
Gráfico de los costos de mano de obra promedio
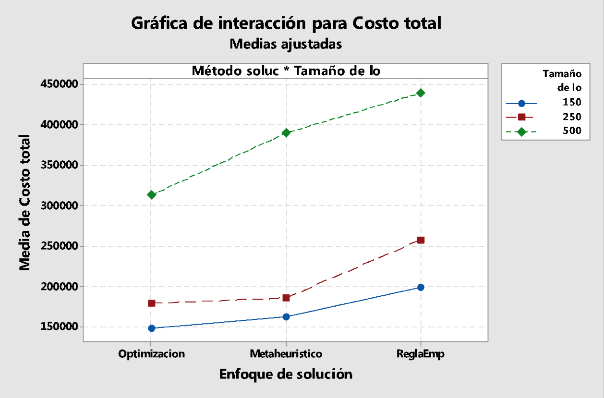
Del gráfico de interacción doble de la Figura 2, se identifica que el enfoque de solución método de optimización genera los menores costos de mano obra promedio para los diferentes tamaños de lote para el acomodo (150, 250 y 500 productos), siendo los menores costos promedio de mano de obra de $150.000, $170.000 y $200.000 respectivamente. Adicionalmente, la reducción en los costos de mano de obra promedio que genera el método de optimización respecto al metaheurístico de búsqueda tabú para los distintos tamaños de lotes de acomodo (150, 250 y 500) es de 10%, 4% y 24% respectivamente; mientras que la reducción de costos del método de optimización respecto a la regla empírica es de 34%, 44% y 40% respectivamente.
De otra parte, estos resultados muestran estadísticamente que el desempeño del metaheurístico de búsqueda tabú es adecuado para tamaños de lotes inferiores a 250 productos mientras que su desempeño es bajo para tamaños de lotes de 500 productos. Se debe resaltar que el metaheurístico de búsqueda tabú presenta mayor eficiencia computacional y mayor capacidad de solución de problemas de slotting de gran tamaño (más de 1.000 productos), lo cual genera ventajas respecto al método de optimización que se limita a problemas de menor tamaño. Esta situación es especialmente relevante en ambientes de almacenamiento donde constantemente se deba calcular la operación de acomodo en un mismo turno de trabajo. Finalmente, se resalta el bajo desempeño de la regla empírica para la solución del problema de slotting, debido a que el método de optimización generan reducciones de costos promedio de mano de obra entre 34% y 44%.
Del artículo se detecta que el problema de slotting no solo impacta en la operación de acomodo sino también en la gestión de la preparación de pedidos para atender los requerimientos de los clientes. De allí, la importancia de las decisiones de esta operación para gestionar adecuadamente la gestión de almacenes considerando costos, nivel de servicio y la eficiencia en general.
El problema de slotting considera diferentes factores que deben incluirse en su modelamiento tales como características del sistema de almacenamiento (volumen en m3) y de los productos (ancho, alto, largo, peso y volumen en m3). Por lo tanto, el problema requiere considerar las restricciones y condiciones logísticas buscando soluciones factibles en la gestión de almacenes.
De la implementación de los enfoques de solución para el problema de slotting, denominados método de optimización, metaheurístico de búsqueda tabú y regla empírica, se identifica del ANOVA que la interacción de doble del factor de método de solución (optimización, metaheurístico y regla empírica) con el factor tamaño de lote de acomodo tiene un efecto significativo sobre el costo total de mano de obra. Adicionalmente, el factor depot no tiene efecto significativo sobre la variable respuesta de interés, de allí, que sea indiferente ubicarlo en el centro o izquierda del almacén en el problema de slotting. Además, la reducción en los costos de mano de obra promedio que genera las combinaciones de los niveles del método de optimización respecto al metaheurístico para los distintos tamaños de lotes de acomodo (150, 250 y 500) son de 10%, 4% y 24% respectivamente. Mientras que la disminución del costo con el método de optimización respecto a la regla empírica es de 34%, 44% y 40% respectivamente.
Finalmente, como trabajo futuro se sugiere integrar otros problemas de gestión de almacenes al slotting, tales como la conformación de lotes con ruteo en el acomodo, buscando así un modelamiento efectivo de la gestión de almacenes. Adicionalmente, considerar otros factores como congestión, y flotas de equipos de manejo de materiales heterogéneos que consideren las características de los productos a manipular.
ARANGO, M., CANO, J. A., & ALVAREZ, K. (2012). Modelos de sistemas MRP cerrados integrando incertidumbre. Revista EIA, 1(18), 61–76.
BARTHOLDI, J. J., & HACKMAN, S. T. (2008). Allocating space in a forward pick area of a distribution center for small parts. IIE - Transactions, 40(11), 1046.
CANO, J. A., GOMEZ, R. A., & SALAZAR, F. (2017). Routing policies in multi-parallel warehouses: an analysis of computing times. Revista Espacios, 38(51), 23. Retrieved from: http://www.revistaespacios.com/a17v38n51/17385123.html
CANO, J. A., PANIZO, C. A., GARCÍA, F. H., & RODRÍGUEZ, J. E. (2015a). Estrategias para el mejoramiento la cadena de suministro del carbón en Norte de Santander, Colombia. Boletín de Ciencias de la Tierra, 1(38), 65–74.
CANO, J. A., PANIZO, C. A., GARCÍA, F. H., & RODRÍGUEZ, J. E. (2015b). Desarrollo de Estrategias Competitivas para la Industria del Carbón en Norte de Santander. Revista Espacios, 36(15), 5. Retrieved from: http://www.revistaespacios.com/a15v36n15/15361506.html
CORREA, A. A., GÓMEZ, R. A., & CANO, J. A. (2010). Gestión de almacenes y tecnologías de la información y comunicación (TIC). Estudios Gerenciales, 26(117), 145–171.
CORTÉS, P., GÓMEZ-MONTOYA, R. A., MUÑUZURI, J., & CORREA-ESPINAL, A. (2017). A tabu search approach to solving the picking routing problem for large- and medium-size distribution centres considering the availability of inventory and K heterogeneous material handling equipment. Applied Soft Computing, 53, 61–73.
FRAZELLE, E. H. (2015). Inventory Strategy: Maximizing Financial, Service and Operations Performance with Inventory Strategy (1st edition). Georgia: McGraw Hill Professional.
GÓMEZ, R. A. (2010). Logística inversa un proceso de impacto ambiental y productividad. Producción + Limpia, 5(2), 63–76.
GÓMEZ, R. A., CANO, J. A., & CAMPO, E. A. (2016). Selección de proveedores en la minería de oro con lógica difusa. Revista Venezolana de Gerencia (RVG), 21(75), 530–548.
GÓMEZ, R. A., GIRALDO, O. G., & CAMPO, E. A. (2016). Conformación de Lotes Mínimo Tiempo en la Operación de Acomodo Considerando k Equipos Homogéneos usando Metaheurísticos. Información Tecnológica, 27(6), 53–62.
GÓMEZ, R., ZULUAGA, A., & CORREA, A. (2014). Propuesta De Sistema De Logística Inversa Para El Sector Hospitalario: Un Enfoque Teórico Y Práctico En Colombia. Ingenierías Usbmed, 5(1), 35–52.
GÓMEZ-MONTOYA, R. A., CORREA-ESPINAL, A. A., & HERNÁNDEZ-VAHOS, J. D. (2016). Picking Routing Problem with K homogenous material handling equipment for a refrigerated warehouse. Revista Facultad de Ingeniería Universidad de Antioquia, (80).
HOU, J.-L., WU, Y.-J., & YANG, Y.-J. (2010). A model for storage arrangement and re-allocation for storage management operations. International Journal of Computer Integrated Manufacturing, 23(4), 369–390.
HERAGU, S. S., DU, L., MANTEL, R. J., & SCHUUR, P. C. (2005). Mathematical model for warehouse design and product allocation. International Journal of Production Research, 43(2), 327–338.
KIM, BYUNG SOO AND JEFFREY S. SMITH. 2012. “Slotting Methodology Using Correlated Improvement for a Zone-Based Carton Picking Distribution System.” Computers & Industrial Engineering 62(1):286–95.
KUTZELNIGG, R. (2011). Optimal allocation of goods in a warehouse: Minimizing the order picking costs under real-life constraints. In Logistics and Industrial Informatics (LINDI), 2011 3rd IEEE International Symposium on (pp. 65–70). IEEE.
MUPPANI, V. R., & ADIL, G. K. (2008). Efficient formation of storage classes for warehouse storage location assignment: a simulated annealing approach. Omega, 36(4), 609–618.
ROJAS, M., GUISAO, E., & CANO, J. A. (2011). Logística Integral: Una propuesta práctica para su negocio. Medellín: Universidad de Medellín.
SALAZAR, F., GOMEZ, R. A., & CANO, J. A. (2017). El problema de carga de pallets en centros de distribución utilizando diseño de mezclas. Revista Espacios, 38(2), 2. Retrieved from: http://www.revistaespacios.com/a17v38n02/17380202.html
TAKAHAMA, HISANORI, TATSUSHI NISHI, MASAMI KONISHI, & JUN IMAI. 2002. “A Determination Method of Product Allocation Schedule for Warehouse Management.” Pp. 1004–7 in SICE 2002. Proceedings of the 41st SICE Annual Conference, vol. 2. IEEE.
1. Politécnico Colombiano Jaime Isaza Cadavid, Colombia. Ingeniero Industrial, PhD en Ingeniería, Industria y Organizaciones. ragomez@elpoli.edu.co
2. Universidad de Medellín, Colombia. Ingeniero Industrial, Magister en Ingeniería Administrativa. jacano@udem.edu.co
3. ESACS – Escuela Superior en Administración de Cadena de Suministro, Colombia. Ingeniero Industrial, Magister en Ingeniería Industrial. emiroa86@hotmail.com