ISSN 0798 1015

Vol. 39 (Nº 15) Año 2018. Pág. 11

Efecto de la Estrategia Instruccional Resolución de Problemas desde una Perspectiva Heurística en el Rendimiento Académico de Cálculo II

Effect of the Instructional Strategy Problem Solving from a Heuristic Perspective on the Academic Performance of Calculus II

Víctor Hugo MERIÑO Córdoba 1; Yamarú del Valle CHIRINOS Araque 2; Carmen Ysabel MARTINEZ de Meriño 3; Claudia Milena PEREZ Peralt 4

Recibido: 29/11/2017 • Aprobado: 19/12/2017

Contenido

1. Introducción

2. Desarrollo

3. Metodología

4. Resultados

5. Conclusiones

Referencias bibliográficas

1. Introducción

En los últimos años la educación Latinoamericana  está inmersa en una profunda crisis, que se refleja en el bajo rendimiento estudiantil, que afecta a todas las instituciones educativas en general, en este sentido los países de América Latina y el Caribe, presentan algunas características similares en el aspecto educativo, todos en común, según el informe de la Organización de Naciones Unidas para la Educación, la Ciencia y la Cultura (Unesco, 2012), tienen problemas de altas tasas de repitencia, exclusión. Ante esta problemática, el Banco Mundial (2009), sostiene que el Sistema Educativo Colombiano no escapa de ella, específicamente en áreas como las ciencias básicas, donde constituye un motivo de preocupación permanente, para todos los que de una u otra forma tienen que ver con el proceso enseñanza – aprendizaje de estas ciencias. Situación a la que tampoco es ajeno el subsistema de educación superior, especialmente en los primeros años de estudios de las carreras, donde se observa que, en los semestres iniciales, en las cuales se estudian asignaturas teórico - práctico como la matemática y las ciencias naturales los resultados son bajos.

En este sentido, Meriño, Taboda & Meriño (2017), afirman que cuando se analiza el proceso instruccional de las ciencias básicas, se observa que confluyen en él, un conjunto de elementos que de alguna manera afectan el aprendizaje de los alumnos, de los cuales se pueden nombrar: (a) las características personales de los estudiantes; (b) las características personales del docente y (c) el enfoque tradicional. Siendo éste último donde el facilitador se considera como poseedor absoluto de la verdad y su misión es transmitirla. El profesor es presionado por los programas y los objetivos previamente establecidos y coloca el acento en los contenidos, descuidando los procesos cognitivos y la capacidad de pensamiento de los alumnos, la cual en lugar de desarrollarse se inhibe y se reduce a solo ejercitar la memorización (Solaz, & Sanjosé, 2008).

Según la evaluación, hecha a 510.000 jóvenes de 15 años, de 65 países, el 74 por ciento de los estudiantes colombianos, es decir, tres de cada cuatro, no tienen las competencias matemáticas básicas para desarrollar las actividades que exige la sociedad contemporánea (Banco Mundial, 2009). En estos resultados se expresa la inexistencia de la capacidad para resolver problemas científicos en nuestros estudiantes, deficiencias directamente relacionadas con el poco, o casi nulo, desarrollo de destrezas mentales de los alumnos en la formación de las ciencias. Tomando en consideración lo antes expuesto, Martínez, Chrinos, & Meriño (2017), sostienen que el aprendizaje de los alumnos del nivel superior, debería organizarse de un modo que prevea el docente un balance entre el que enseña, cómo y para qué, especialmente en algunas asignaturas, de carácter teórico práctico, como es el caso de las ciencias, caracterizada por altos porcentajes de aplazados a nivel nacional.

Como evidencia de la afirmación anterior, diversos organismos del país han emitido juicios e informaciones estadísticas en relación a la calidad de la educación, medida por los resultados de las pruebas de aprendizajes tanto nacionales como internacionales, muestra algunos signos de mejora. Los resultados de las pruebas PISA para los años 2006 y 2009 registran aumentos en las tres áreas (matemáticas, lectura y ciencias).  No obstante, el país se ubica en los rangos inferiores entre los países participantes y por debajo de países latinoamericanos como Chile, México y Argentina (OECD, 2010).

Como dato complementario a lo anterior, podemos señalar un análisis del PISA de 2006, que muestra que el desempeño de Colombia es pobre y está por debajo de su potencial en relación con su nivel de ingresos. Colombia se desempeñó muy abajo del promedio general entre los 57 países participantes de este Programa y por debajo de la media entre los países de América Latina y el Caribe, aunque sus resultados fueron mejores que Argentina en lectura y parejos con Brasil en matemáticas. Estos resultados pueden no sorprender, ya que los ingresos nacionales per cápita tienden a correlacionarse con el desempeño y teniendo en cuenta que Colombia fue sólo uno de los seis países de ingresos medianos bajos en participar en el PISA (Banco Mundial 2009). En este orden de ideas, Marín, Nieles, Sarmiento & Valbuena (2017), identifican que el informe PISA, centró su atención en evaluar las competencias que desarrollan los jóvenes, asociadas a sus capacidades para concebir la lectura como vía que posibilita su acceso al logro de metas e intereses personales; de los resultados se desprende que el 47 % de los estudiantes colombianos no alcanzó el nivel 2 (mínimo esperado); situación similar se presenta en cuanto al razonamiento lógico – matemático, así como también la resolución creativa de problemas cotidianos, con complejidad variada, en un contexto global. 

Por todo lo anterior, el análisis del PISA de 2006 se concentró en el estudio del desempeño en matemáticas, ya que son éstas las que permiten medir la aptitud para resolver problemas, uno de los atributos más importantes en el aprendizaje (Banco Mundial 2009). Como puede notarse, en la misma vía de análisis de la situación de los alumnos, con respecto al aprendizaje de matemática, hay una persistencia de la problemática, aún entre estudiantes, considerados con promedios globales, que están en la jerarquización de los exigibles para presentar pruebas de opción de ingreso en la referida institución considerada exigente. Esto pudiese constituir un reflejo de las condiciones en las cuales se encuentra el aprendizaje de la matemática no sólo se evidencia a nivel internacional, nacional sino también regional (Villalobos, 2008).

En este mismo orden de ideas, una de las asignaturas donde mayor se refleja la situación de angustia que vive el docente, por el bajo rendimiento estudiantil,  es sin lugar a dudas el cálculo II y la Corporación  la Universitaria del Caribe (CECAR), no escapa a esta problemática, según se refleja en la estadística de la Dirección de Admisiones, Registro y Control Académico de la Corporación,  en la cátedra cálculo II,  donde se  han  inscrito 398 alumnos desde 2014 hasta el primer periodo de 2016, de los cuales han aprobado  298, lo que representa el 74,87%, pero con un promedio de 3,23 puntos, donde la nota mínima aprobatoria es 3 puntos y la máxima puntuación es 5 puntos. Notándose un bajo rendimiento estudiantil. Está situación obliga a las distintas dependencias de esta institución a estudiar las causas de este fenómeno, para determinar según los resultados, el grado de eficacia de los planes, programas, estrategias, técnicas y recursos utilizados en los aprendizajes de la asignatura, para así introducir cambios o ajustes convenientes.

Al respecto, Meriño, Taboda & Meriño (2017), exponen,  que  los alumnos manifiestan quejas frecuentes de cambios constantes de actitud por parte de algunos docentes y la utilización de estrategias instruccionales que abruman al estudiante porque no estimulan a desplegar la autonomía, el uso de la imaginación, a aprender a aprender, sino que se limitan a la transmisión y repetición memorística de la información, coadyuvando  que el estudiante se comporte como ente pasivo dentro del proceso enseñanza - aprendizaje y subordinado totalmente a la autoridad del profesor quien se considera poseedor absoluto de la verdad.

En este sentido, González (2014), expresa que con el método memorístico el alumno aprende a recitar contenidos matemáticos, pero esto no significa que han aprendido matemática puesto que el aprendizaje en esta asignatura se mide por la capacidad para resolver problemas, lo que trae como consecuencia un bajo rendimiento académico en vista de que no se produce un verdadero aprendizaje de los contenidos.

Al respecto, se puede decir que, aunque es necesario memorizar muchas ideas, conceptos y principios para resolver problemas, más importante es saber las condiciones como se han aprendido, haciendo énfasis en los procesos internos del organismo en interacción con factores externos para llegar a esa última etapa donde se han desarrollado aprendizajes en forma jerárquica (Alcalde, Aguilar, Navarro & López, 2002). Así mismo, según Martínez, Chirinos & Meriño (2017), el aprendizaje se activa por medio de una variedad de clases de estimulación procedente del ambiente del estudiante, la cual es la energía absorbida por los procesos de aprendizaje cuya potencia generada constituye una modificación del comportamiento que se observa como una actuación humana. Se hace entonces impostergable introducir cambios que permitan al docente y alumno asumir nuevos roles dentro del proceso enseñanza-aprendizaje de la matemática, desarrollar estrategias tanto de enseñanza como de aprendizaje que se correspondan con el carácter activo y práctico de la Matemáticas y con la forma constructiva, creadora y significativa que tiene el hombre de aprender. Ante esta situación planteada y teniendo en cuenta la complejidad del fenómeno educativo y la serie de factores que pudieran estar incidiendo en el aprendizaje de la matemáticas referidas (al alumno, el docente, y el medio), se hace necesario poner en práctica estrategias de aprendizaje en función de los objetivos de la disciplina, características de los estudiantes, ámbito socio-económico, ambiental y cultural, disponibilidades matemáticas y presupuestarias; orientada a la misma hacia el enfoque activo y práctico del aprendizaje así como a la forma de aprender constructiva del hombre.

Como alternativa de solución al problema antes descrito, se considera pertinente para el aprendizaje de la matemáticas otro enfoque diferente al tradicional así como lo considera González (2014), al señalar que los aprendizajes de la matemáticas con la “estrategia instruccional resolución de problemas desde una perspectiva heurística”, constituye un proceso mediante la cual, los estudiantes exploren ideas matemáticas a través de actividades centradas en ellos (descubrimiento o indagación de conceptos, principios y patrones, demostración, estudios individualizado o en grupos, solución de problemas), sin apartar la función indispensable de la participación de docente como: planificador, organizador, evaluador, facilitador y orientador del proceso; aplicando combinadas técnicas, (dinámicas grupales, demostración resolución de problemas), con otro enfoque adecuado al acto educativo.

Bajo esta concepción, el salón de clases, no es sólo un ambiente físico, sino un modo de abordar la enseñanza y el aprendizaje de las matemáticas. Con la aplicación de la estrategia instruccional resolución de problemas desde una perspectiva heurística, se pretende mantener motivado al alumno de matemáticas, logrando aprendizajes integrales, debido a que con su participación activa en el proceso, no solamente explorará, descubrirá y desarrollará conocimientos, habilidades intelectuales, estrategias cognoscitivas sino que alcanzará progresivamente destrezas y actitudes ligadas a sus necesidades e intereses y los de la sociedad, formando el hombre integral ideal que requiere nuestra sociedad.

1.1. Objetivo general

Determinar los efectos de la aplicación de la estrategia instruccional resolución de problemas desde una perspectiva heurística en el rendimiento académico de los estudiantes de cálculo II de ingeniería industrial de la Corporación Universitaria del Caribe, durante el primer período de 2016

2. Desarrollo

2.1. Estrategia instruccional resolución de problemas desde una perspectiva heurística.

Se considera la heurística como un método para resolver problemas matemáticos, en esta línea de pensamiento, la estrategia instruccional resolución de problemas desde una perspectiva heurística permite al sujeto seleccionar dentro de que límites mantendrá su búsqueda. La heurística es un método no riguroso para obtener soluciones de problemas, que deben ser sometidas a comprobación (Alonso & Martínez, 2003).

Santos (2007), señala que un descubrimiento resuelve un gran problema, pero en la solución de todo problema, hay un cierto descubrimiento. El problema que se plantea puede ser modesto; si pone a prueba la curiosidad que induce a poner en juego las facultades inventivas, si se resuelve por propios medios, se puede experimentar el encanto del descubrimiento y el goce del triunfo. Experiencias de este tipo, a una edad conveniente, pueden determinar una afición para el trabajo intelectual e imprimirle una huella imperecedera en la mente y en el carácter.

Al respecto, Alcalde, Aguilar, Navarro & López (2002), sostienen que, un estudiante cuyos estudios incluyan cierto grado de matemáticas tiene también una particular oportunidad, ésta se pierde, claro está, si ve la matemática como una materia de la que tiene que presentar un examen final y de la cual no volverá a ocuparse una vez pasado éste, la oportunidad puede perderse incluso si el estudiante tiene un talento natural para las matemáticas, ya que él, como cualquier otro, debe descubrir sus capacidades y sus aficiones; no puede saber si le gusta el pastel de frambuesas si nunca lo ha probado. Puede descubrir, sin embargo, que de un problema de matemática puede ser tanto o más divertido que un crucigrama, o que un vigoroso trabajo intelectual puede ser un ejercicio tan agradable como un ágil juego de tenis. Habiendo gustado del placer de las matemáticas, ya no las olvidará fácilmente, presentándose entonces una buena oportunidad para que la matemática adquieran un sentido para él, ya sean como un pasatiempo o como herramienta de su profesión, o su profesión misma o la ambición de su vida. 

La heurística tiene múltiples ramificaciones: los matemáticos, los logísticos, los psicólogos, los pedagogos e incluso los filósofos, pueden reclamar varias de sus partes como pertenecientes a su dominio especial. Una experiencia que resulta a la vez de la solución de problemas y de la observación de los métodos del prójimo, constituye la base sobre la cual se construye la heurística. La heurística coadyuva a una mejor comprensión de las operaciones mentales típicamente útiles en la solución de un problema, puede en efecto, influir favorablemente en los métodos de la enseñanza, en particular en lo que se refiere a las matemáticas (Sepúlveda, Medina, & Sepúlveda, 2009). En este sentido, Alonso & Martínez (2003), enfatizan que la estrategia instruccional desde una perspectiva heurística, proporciona al estudiante el hecho de seleccionar las alternativas mediante un razonamiento provisional plausible que facilite el descubrimiento de la solución. El alumno puede ser guiado o el mismo decidir a donde llevar la búsqueda, cuando planifica la solución del problema. La estrategia instruccional resolución de problemas desde una perspectiva heurística, conduce al estudiante a trabajar resolviendo problemas usando discriminaciones, conceptos y principios. Analiza los procesos empleados comprendiendo su razonamiento de solución.

En relación con el aprendizaje de la matemática, utilizando la estrategia instruccional desde una perspectiva heurística, facilita los siguientes alcances: 1. Individualiza y personaliza el aprendizaje por los alumnos. 2. Logra un llamado a la actividad personal y a la participación en el aprendizaje. 3. Entrena para aprender por sí mismo. 4. Hace sentir la unidad estructural de los problemas. 5. Permite comprender la matemática al mismo tiempo que logra ciertos algoritmos y la heurística. 6. Se aprecia el conocimiento como algo a la vez abstracto y una herramienta útil para alcanzar la realidad. 7. Facilita el desarrollo de la inteligencia y del pensamiento creador y crítico. 8. Se logran plantear problemas pertinentes a la sociedad y en los cuales el conocimiento adquirido en nivel superior, pueda ser útil (Castro, 2008).

Para resolver problemas aplicando esta estrategia instruccional, es importante que el estudiante lea en voz alta y con la adecuada inflexión del problema en los términos planteados. No sólo debe aprender a leer, a comprender los problemas, para lograr que sea capaz de detectarlos, plantearlos en términos comprensibles para otros (Pérez, & Ramírez, 2011).

Según, Meriño, Taboda & Meriño (2017), para solucionar un problema, se debe planificar de la siguiente manera:

Comprensión del problema: es la regla uno, el estudiante aprende a comprender el problema a través de las siguientes interrogantes: ¿cuál es la incógnita? ¿Cuáles son los datos? ¿Cuál es la condición? ¿Es la condición suficiente para determinar la incógnita? ¿Es suficiente? ¿Redundante? ¿Contradictoria?

Concepción de un plan: comprendido el problema, debe lograr programar lo que debe hacer para alcanzar la solución y por lo tanto concibe un plan a través de las siguientes interrogantes: ¿se ha encontrado con un problema semejante? ¿O ha visto el mismo problema planteado en forma ligeramente diferente? ¿Conoce un problema relacionado con éste? ¿Conoce algún teorema que le pueda ser útil?, mire atentamente la incógnita y trate de recordar un problema que le sea familiar y que tenga la misma incógnita o similar, ¿podría usted utilizarlos? ¿le haría falta algún elemento auxiliar a fin de poder utilizarlo? ¿Puede enunciar el problema de otra forma? ¿Ha intentado todos los datos? ¿Ha considerado usted todas las nociones esenciales (datos, conceptos y principios) concernientes al problema?

Ejecución del plan: una vez concebido el plan de acción dividido el problema en sub-problemas, organizada una secuencia de solución y compruebe cada uno de los pasos, ¿puede ver claramente que el procedimiento es correcto? ¿Puede usted demostrarlo?

Visión retrospectiva: esta etapa, es sin duda, la que convierte esta metodología en una óptima alternativa de solución de las estructuras del pensamiento, pues, se trata de auto-analizar su actividad y lograr una visión retrospectiva a través de las siguientes interrogantes: ¿puede usted verificar el resultado? ¿Podría verificar el razonamiento? ¿ha empleado el método en otro problema?

Figura 2
Estrategia resolución de problemas desde una perspectiva heurística

Fuente: elaboración propia.

La estrategia resolución de problemas desde una perspectiva heurística, se puede resumir en cuatro pasos:

1. Comprensión del problema: familiarizarse con el problema

1. ¿por dónde debo empezar?, empieza por el enunciado del problema.
2. ¿qué puedo hacer?  trata de visualizar el problema como un todo, tan claramente como pueda. No se preocupe, preocúpese por los detalles, por el momento.
3. ¿qué gano haciendo esto?, comprenderá el problema se familiarizará con él, grabando su propósito en su mente, su memoria y prepararla para recoger los puntos importantes.

2. Concebir un plan: en busca de una idea útil

1. ¿por dónde empezar?, empiece por considerar los elementos principales del problema. Comience cuando dichas partes estén, por usted, claramente dispuestas y concebidas, gracias a su trabajo previo.
2. ¿qué puedo hacer?, ¿considere el problema desde varios puntos contactos con sus conocimientos previamente adquiridos? Vea el problema desde distintos ángulos. Subraye las diferentes partes, examine los distintos detalles, revise los mismos repetidamente, pero de modo variado, combine entre sí, éste de diversas maneras, abórdelos de diferentes lados. Trate de ver algún nuevo significado en cada detalle, de alguna interpretación del conjunto.
3. Busque puntos de contacto con sus conocimientos previamente adquiridos, trate de acordarse de lo que ayudó en el pasado ante circunstancias análogas. Reconozca algo familiar en lo que examina y de encontrar algo útil en lo que reconoce.
4. ¿Qué puedo encontrar?, una idea que le sea útil, quizás ésta le muestre de golpe como llegar a la solución misma del problema.
5. ¿Cómo puede ser útil una idea?, haciéndole ver el conjunto del razonamiento ó una parte de él. Le sugiere más o menos claramente cómo puede proceder. Es una suerte tener una idea sea cual fuere ésta.
6. ¿Qué puedo hacer con una idea incompleta?, la debe considerar. Si parece ventajosa, la debe tomar en cuenta más a fondo. Si es para digna de confianza, usted debe averiguar la situación. Puede que cambien gracias a su idea útil. Considere la nueva condición desde varios puntos de vistas y busque las partes de contacto con sus conocimientos adquiridos anteriormente.
7. ¿Qué gano haciendo esto nuevamente?, puede usted tener la suerte de encontrar alguna otra idea. Quizás su nueva intención lo conduzca directamente al camino de la solución. Tal vez requiere usted algún esbozo más. Incluso, alguna de éstas ideas le desvía a usted el camino correcto. No obstante, debe alegrarse todo nuevo plan que surja, también por la poca importancia o confusa, y por consiguiente los proyectos suplementarios que añaden alguna precisión a una intensión confusa o permitan la corrección de una idea menos afortunada. Incluso si por cierto tiempo no se le presenta un nuevo esbozo verdaderamente bueno, considérese afortunado si su concepción del problema se torna completa o más coherente, más homogénea o mejor equilibrada.

3. Ejecución del plan

¿Por dónde debo empezar?, empiece por la feliz idea que le conduce a la solución, comience cuando esté seguro de tener correcto punto de partida y esté confiado de poder suplir los detalles menores que puedan necesitarse.

¿Qué puedo hacer?, asegúrese de que tiene plena comprensión del problema. Efectúe en detalles todas las operaciones algebraicas o geométricas que previamente ha reconocido como factibles adquiere la convicción de la exactitud de cada paso mediante un razonamiento formal o por discernimiento intuitivo o por ambos medios, si es posible. Si su problema es muy complejo, usted puede distinguir “grandes” pasos y “pequeños” procedimientos, estando compuesto cada proceso de varios pequeños. Compruebe primero los grandes pasos y después considere los menores.

¿Qué gano haciendo esto?, una presentación de la exactitud y corrección de cada paso no ofrece duda alguna.

4. Visión retrospectiva. (Evaluación)

¿Por dónde debo empezar?, por la solución completa y correcta en todos los detalles.

¿Qué puedo hacer? Considerar la solución desde varios puntos de vista y buscar los puntos de contacto con sus conocimientos previamente adquiridos. Considere los detalles de la solución y trate de hacerles tan sencillos como pueda; reconsidérelos más extensamente y logre condensarlos; para abarcar de un vistazo la solución completa. Trate de modificar, en beneficios de ellas, tanto las partes principales como las secundarias y mejore la solución en su conjunto de tal modo que se adivine por sí misma y que quede grabada, en forma natural, en el cuadro de sus conocimientos previos examine atentamente el método que le ha llevado a la solución, capte su razón de ser y de aplicarlo a otros problemas similares.

¿Qué gano haciendo esto?, puedo encontrar una solución mejor y diferente, descubrir nuevos hechos interesantes. En todo caso, si toma el hábito de reconsiderar las soluciones y examinarlas muy atentamente, adquiere usted una serie de conocimientos correctamente ordenados, utilizables en cualquier momento, a la vez que desarrolla su aptitud en la resolución de problemas.

2.2. Rendimiento académico

El rendimiento académico puede considerarse como indicador de la productividad de un sistema educativo donde se interrelacionan operadores o prestantes: docentes, administradores, obreros o usuarios: estudiantes, comunidades y unas condiciones espacio - temporales de operación o de contexto del proceso, el cual es de carácter socioinstitucional, ya que abarca influencias provenientes de la estructura de la sociedad y de la estructura institucional Meriño, Taboda & Meriño (2017). En tal sentido, se analizan los factores que determinan el rendimiento académico:

a.- Características del estudiante

Son todos aquellos rasgos que determinan las diferencias individuales y son inherentes al participante. Entre estos pueden mencionarse los siguientes: 1.- Conductas de entrada o pre-requisitos que el estudiante posee al abordar la experiencia de aprendizaje.  2.- Habilidades generales para el aprendizaje y capacidades de autodirección para el estudio. 3.- Grado de implicación en el proceso, el cual depende de la motivación y desarrollo de la autonomía.

b.- Características de los docentes

Comprenden los rasgos profesionales, personales y académicos- docentes del facilitador. Entre ellos: 1.- Dominio del contenido de las asignaturas que imparten. 2.- Dominio de la Tecnología Educativa (diseño curricular, planificación, metodología de enseñanza-aprendizaje, evaluación, recursos   instruccionales, comunicación didáctica. 3.- Formación interdisciplinaria, humanística, profesional social. 4.- Grado de implicación psico- afectiva en el proceso. 5.- Habilidades de Comunicación a nivel profesional y grupal. 6.- Rasgos del docente y etapas del proceso educativo.

c.- Contexto instruccional

Comprende ambiente espacio temporal, reglamentos, normas que se transforman en marco referencial para las relaciones facilitador- participante, docente- docente, estudiante- estudiante. Incluye: 1.- Política–planes y programas de la institución. 2.- Desarrollo Curricular. 3.- Soporte Administrativo.  4.- Servicios de apoyo al estudiante.

d.- Factores propios del estudiante que determinan sus logros académicos

Muchas veces nos preguntamos, el por qué los estudiantes rinden en forma tan variada, y cuáles elementos intervienen en esa diversidad de respuestas, es decir, que factores determinan sus logros académicos. Al respecto, Meriño, Taboda & Meriño (2017), establecen una serie de factores que influyen en el rendimiento académico de los estudiantes: 1.- Factores ambientales.  2.- Características del Estudiante.  3.-características Docentes. Para una mayor y mejor visualización de estos factores se presenta la siguiente ilustración:

Figura 1
Factores que afectan al rendimiento estudiantil

Fuente: Meriño, Taboda & Meriño (2017)

Según Meriño, Taboda & Meriño (2017), el rendimiento estudiantil en Colombia, se mide por medio de las calificaciones obtenidas por el participante durante su recorrido por la Universidad, es decir, desde que se inicia en el primer semestre hasta que culmina su último semestre aprobado, dentro de una escala de cero (0) a cinco (5) puntos. Esta variable presenta algunos aspectos que condicionan los resultados académicos tales como: la preparación del docente, dominio de los recursos instruccionales, conocimiento de la asignatura que dicta, grado de interacción e integración entre los facilitadores y participantes y el nivel socioeconómico de los participantes.

Estrategia resolución de problemas desde una perspectiva heurística y el rendimiento académico

Las estrategias que ofrezca el facilitador, pueden surtir efectos en el estudiante y por consiguiente en su rendimiento académico (Puig, 2008). No se puede desligar el rendimiento académico de la eficacia del docente, porque una es consecuencia de la otra. Si el profesor no maneja las estrategias adecuadas y no está actualizado con las innovaciones que en el campo educativo se han producido no podrá alcanzar el nivel de preparación que la sociedad le demanda para insertarse en el desarrollo. Al respecto, Meriño, Taboda & Meriño (2017), sostienen que el rendimiento estudiantil podrá entenderse como el resultado del proceso enseñanza- aprendizaje, mediante el cual el docente puede determinar si el conocimiento que él ha transmitido ha sido comprendido y asimilado por el alumno. Por consiguiente, puede considerarse el rendimiento académico como el resultado del proceso de aprendizaje, a través del cual el asesor puede determinar en qué cantidad y calidad, el aprendizaje facilitado ha sido internalizado por el participante. Al respecto, Meriño, Taboda & Meriño (2017), afirman que el rendimiento estudiantil podrá entenderse como el resultado del proceso enseñanza- aprendizaje, mediante el cual el docente puede determinar si el conocimiento que él ha transmitido ha sido comprendido y asimilado por el alumno.

Por consiguiente, puede considerarse el rendimiento académico como el resultado del proceso de aprendizaje, a través del cual el asesor puede determinar en qué cantidad y calidad, el aprendizaje facilitado ha sido internalizado por el participante. Por lo tanto, el objetivo principal del rendimiento académico en este caso es comparar los objetivos propuestos en el material instruccional con los resultados del aprendizaje alcanzado por el participante. Para llevar a cabo tal comparación para juzgarla con propiedad y poder utilizar los resultados, el asesor debe recurrir a una serie de medios que le permitan evaluar y registrar las características y aprovechamiento académico del participante.

3. Metodología

3.1. Tipo de investigación

Esta investigación se clasificó siguiendo diversos criterios. Por su propósito,  es de carácter aplicada, debido a que “se le dará solución al problema formulado en un lapso corto de tiempo” (Chávez, 2014).por el período en el que se recolectó la información, se considera prospectiva, en razón a que “todos los datos recolectados  se procesaron de acuerdo con los criterios establecidos por el investigador, previa planificación del estudio” (Méndez, Moreno, Nanhira & Sosa, 2014); por la comparación de las muestras, se tipifica como comparativo, porque “se efectúan comparaciones de los efectos entre las variables y niveles de éstos”.  Según el método de investigación, es de tipo cuasi experimental, porque “se manipulará la variable independiente: la aplicación de la estrategia instruccional resolución de problemas desde una perspectiva heurística, aunque no se seleccionaron aleatoriamente los sujetos de la muestra, se ubicaron respectivamente en los grupos de control y experimental y se controlaron algunas variables que pudieron contaminar el efecto de la variable experimental” (Chávez, 2014).

3.2 Población

La población objeto de estudio estuvo constituida por 104 estudiantes cursantes del I semestre académico del año 2016, de la asignatura cálculo II correspondiente al segundo semestre de la Facultad de Ciencias Básicas, Ingeniería Industrial y Arquitectura, de la Corporación Universitaria del Caribe, ubicada en el Municipio Sincelejo, Departamento de Sucre, Colombia.

3.3 Muestra

Dos secciones de 52 alumnos cada una, una fue el grupo experimental y la otra el grupo control.

3.4 Diseño de la investigación

El diseño de la investigación seleccionado correspondió a uno cuasi-experimental, con Pre-test y Post-test y dos grupos de comparación; el experimental o de comparación y el de control.

Tabla 1
Análisis del rendimiento académico de los grupos experimental y control después
de la aplicación de las estrategias resolución de problemas desde una perspectiva
heurística y tradicional a los estudiantes de cálculo II

Fuente: elaboración propia.

En cuanto a la variable rendimiento académico, los estudiantes del grupo experimental lograron mayor rendimiento académico que los del grupo control, es decir, los estudiantes del grupo experimental tienen un promedio de   = 4,28 puntos y los estudiantes del grupo control tienen un promedio de   = 3.23 puntos.

Tabla 2
Análisis del Post test de los grupos experimental y control después de la aplicación
de las estrategias resolución de problemas desde una perspectiva heurística
y tradicional a los estudiantes de cálculo II

Fuente: elaboración propia.

Se puede evidenciar que en todos los indicadores los valores de t–Student calculados superan al valor crítico positivo interpolado, lo cual demuestra que hay diferencias altamente significativas entre el grupo experimental y el grupo control para un nivel de significación de 0.05. A la vez se verifica que los valores calculados caen en la región de rechazo cola a la derecha, lo que significa que los estudiantes del grupo experimental resuelven mejor los problemas que los estudiantes del grupo control al comprobarse que la media aritmética del grupo experimental es mayor que la del grupo control, es decir, los estudiantes: a) casi siempre se disponen a comprender un problema, b) siempre pueden concebir un plan para resolver un problema. c) siempre pueden ejecutar el plan concebido para resolver un problema y d) casi siempre pueden evaluar el proceso antes, durante y después de resolver un problema

Para comprobar la validez de las anteriores aseveraciones se procede a aplicar un análisis de varianza por dimensión.

Las hipótesis son las siguientes:

Tabla 3
Análisis de varianza de los Grupos experimental y control después de la aplicación
de las estrategias resolución de problemas desde una perspectiva heurística
y tradicional a los estudiantes de cálculo II

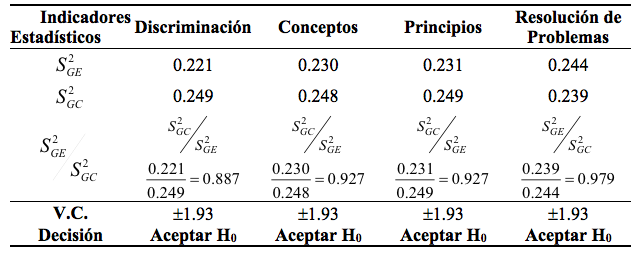
Fuente: Elaboración propia.

Por tanto, de acuerdo a lo establecido en el cuadro anterior, se evidencia en todas las dimensiones que el valor F calculado es menor al valor crítico, aceptando H0, en consecuencia, las pruebas t–Student son válidas.

Después de analizar los resultados obtenidos atendiendo a los objetivos propuestos se llegó a las siguientes conclusiones: 

Se determinó que con la aplicación de la estrategia instruccional resolución de problemas desde una perspectiva heurística, los alumnos del grupo experimental tienen pocas dificultades para: descubrir conceptos, descubrir reglas y principios y resolver problemas, caso opuesto los participantes del grupo control que tienen muchas dificultades para: descubrir conceptos, descubrir reglas y principios y resolver problemas.

Con respecto a los resultados que se obtuvieron en el rendimiento académico de los estudiantes cálculo II del grupo experimental, lograron ubicarse en un promedio de 4.28; mientras que los pertenecientes a los del grupo de control, se lograron ubicar en un promedio de 3.23.

En general, en el grupo experimental se observó una supremacía, estadísticamente hablando, con la aplicación de la estrategia instruccional resolución de problemas desde una perspectiva heurística y en el rendimiento académico en cálculo II, se presume que este resultado es producto de la aplicación la aplicación de la estrategia instruccional resolución de problemas desde una perspectiva heurística, no así en el grupo control, a los cuales se le administró la estrategia tradicional de enseñanza.

Alcalde, C.; Aguilar, M.; Navarro, J. & López, J. (2002). Pensamiento formal y resolución de problemas matemáticos. Psicothema, España, p. 382-386.

Alonso, I. & Martínez, N. (2003). La resolución de problemas matemáticos. Una caracterización histórica de su aplicación como vía eficaz para la enseñanza de las matemáticas. Revista pedagogía universitaria, 8 (3).

Banco Mundial (2009).   La   calidad   de   la educación en Colombia: un análisis y   algunas    opciones   para   un programa de política.  Editorial del Banco Mundial, USA

Castro, E. Resolución de problemas. (2008).  Ideas, tendencias e influencias en España., Actas del XIII Simposio de la SEIEM. Badajoz-España, p. 93-111.

CECAR (2015). Análisis de la situación estudiantil en ciencias básicas. Sincelejo, Sucre, Colombia.

Chávez, N. (2014). Introducción a la investigación educativa. 2da. Edición. Maracaibo: Editorial ARS Gráfica Maracaibo.

González, F. (2014). La enseñanza de la matemática con un enfoque de laboratorio. Maturin. Venezuela

Marín, F; Nieles, M.; Sarmiento, M. & Valbuena, S. (2017). Mediación de las tecnologías de la información en la comprensión lectora para la resolución de problemas aritméticos de enunciado verbal. Vol. 38 (Nº 20), Año 2017. Pág. 19. Recuperado de: http://www.revistaespacios.com/a17v38n20/17382020.html

Martínez, C., Chirinos, Y. & Meriño, V. (2017). Innovaciones educativas en la educación básica. En Meriño, V., Chirinos Y., Camejo. L., & Martínez, C. (Ed.) Gestión del Conocimiento Perspectiva Multidisciplinaria. (36 – 58). Coro. Venezuela: Fondo Editorial Servando Garcés.

Méndez, I; Moreno, L; Namhira, D. & Sosa, C. (2014). El protocolo de investigación: lineamientos para su elaboración y análisis. Editorial Trillas. México.

Meriño, V., Taboda, R. & Meriño. (2017). Estrategia con un enfoque laboratorio en el rendimiento académico del álgebra lineal. En Meriño, V., Chirinos Y., Camejo. L., & Martínez, C. (Ed.) Gestión del Conocimiento Perspectiva Multidisciplinaria. (73 – 103). Coro. Venezuela: Fondo Editorial Servando Garcés.

OCDE. (2010).  Panorama de la educación: Indicadores de la OCDE.

Pérez, Y. & Ramírez, R. (2011). Estrategias de enseñanza de la resolución de problemas matemáticos: Fundamentos teóricos y metodológicos. Revista de Investigación, 35(73), 169-194. Recuperado en 30 de marzo de 2016, de http://www.scielo.org.ve/scielo.php?script=sci_arttext&pid=S1010-29142011000200009&lng=es&tlng=es.

Puig, L. (2008). Resolución de problemas: 30 años después. Actas del XIII Simposio de la SEIEM. Badajoz-España, p.93-111

Santos, M. (2007).  La resolución de problemas matemáticos. Trillas. México.

Sepúlveda, A., Medina, C. & Sepúlveda, D. (2009). La resolución de problemas y el uso de tareas en la enseñanza de las matemáticas. Educación matemática, 21(2), 79-115. Recuperado en 16 de noviembre de 2017, de http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S1665-58262009000200004&lng=es&tlng=es.

Solaz, J. & Sanjosé, V. (2008). Conocimiento previo, modelos mentales y resolución de problemas. Un estudio con alumnos de bachillerato. Revista Electrónica de Investigación Educativa, 10 (1). Consultado el día 16 de noviembre de 2017 en: http://redie.uabc.mx/vol10/no1/contenido-solaz.html

UNESCO (2012). Informe educación para todos. USA.

Villalobos, X. (2008). Resolución de problemas matemáticos: un cambio epistemológico con resultados metodológicos. REICE. Revista iberoamericana sobre calidad, eficacia y cambio en educación, Madrid, España, p. 36-58.

Citation

MERIÑO, Víctor H; CHIRINOS, Yamarú, Del V; MARTINEZ, Carmen Y; y PEREZ, Claudia M. Efecto de la estrategia instruccional resolución de problemas desde una perspectiva heurística en el rendimiento académico de cálculo II. Revista Espacios. Vol 39, Año 2018, Numero 15, Pagina.11. Recuperado de: http://www.revistaespacios.com

1. Licenciado en Matemática de la Universidad del Zulia, Magister en Docencia Universitaria de la Universidad Nacional Experimental Rafael María Baralt, Doctor en Educación de la Universidad Privada Dr. Rafael Belloso Chacín. Investigador Senior categorizado por Colciencias. Docente- investigador del grupo: GORAS. Universidad Católica Luis Amigó. Medellín – Colombia. Email victor.merinoco@amigo.edu.co   ORCID ID. 0000-0001-8911-7202

2. Licenciada en Administración Industrial, de la Universidad Nacional Experimental Rafael María Baralt Magister en Docencia Universitaria, de la Universidad Nacional Experimental Rafael María Baralt, Doctora en Gestión de la innovación, de la Universidad Privada Dr. Rafael Belloso Chacín. Investigadora Asociada categorizada por Colciencias. Docente- investigador del grupo: GORAS. Universidad Católica Luis Amigó.  Medellín – Colombia. Email yamaru.chirinosar@amigo.edu.co   ORCID ID. 0000-0003-0471-9859.

3. Licenciada en Comercio del Instituto Universitario Pedagógico Monseñor Arias Blanco, Magister en Docencia Universitaria de la Universidad Nacional Experimental Rafael María Baralt, Doctora en Educación de la Universidad Privada Dr. Rafael Belloso Chacín. Investigadora Categorizada Asociada por Colciencias. Docente Investigador Universidad Católica Luis Amigó.  Medellín – Colombia. Email cimartinezunermb@gmail.com ORCID ID. 0000-0002-8134-2306.

4. Magister en Economía, de la Universidad de Manizales, Magister en Negocios Internacionales e Integración de la Universidad Tecnológica de Bolívar y Magister en Educación de la Universidad de Sucre. Investigadora Categorizada Junior por Colciencias. Docente Investigador Email milena.claudia@gmail.com ORCID ID.  0000-0002-3799-9642