

Vol. 39 (Nº 13) Año 2018 • Pág. 29
Julian PAREJA Vasseur 1; Julio Aníbal BAENA A. 2
Recibido: 19/11/2017 • Aprobado: 12/12/2017
RESUMEN: Este artículo se fundamentó en estimar de manera experimental, el coeficiente de aversión al riesgo utilizando la función de aversión relativa al riesgo constante (constant relative risk aversion o CRRA). La metodología utilizada fue mediante el método de pares de loterías aleatorias en grupos a pequeña escala. Los resultados permitieron estimar el coeficiente de aversión al riesgo mediante la calibración de la función CRRA. Para futuras investigaciones se promueve el uso de otro tipo de funciones. |
ABSTRACT: This article was based on estimate on an experimental basis, the coefficient of risk aversion using the constant risk aversion (CRRA). The methodology used was by the method of pairs of random lotteries in groups on a small scale. The results allowed to estimate the coefficient of risk aversion through the calibration of the CRRA. For future research promotes the use of another type of functions. |
En economía, al momento de construir la teoría del consumidor es posible encontrar múltiples supuestos, entre ellos, uno considera al individuo como un ser que desea mediante su conducta, elegir entre diferentes cestas de consumo, las cuales le permiten obtener el mayor bienestar y por lo tanto maximizar su utilidad.
La literatura relaciona autores como Cohn, Lewellen, Lease y Schlarbaum (1975), quienes desarrollaron los axiomas de preferencia de la racionalidad, que se consideran como una primera aproximación para entender el comportamiento racional del individuo; su idea básica parte de comparar dos cestas de consumo, cuyas respectivas combinaciones proporcionan el mismo nivel de bienestar y son las que terminan dando origen a las curvas de indiferencia. En este orden de ideas, una manera de cuantificar el bienestar, medido a través de dichas curvas, corresponde la construcción matemática conocida como función de utilidad, la cual se define como una abstracción numérica que permite medir la satisfacción que obtiene un agente económico, a través del consumo de determinada cantidad de bienes. Alchian (1953) explicó la relevancia de medir dichas funciones como resultado de las preferencias del individuo; por lo que es plausible argumentar que cada persona posee una función de utilidad que mide su bienestar, la cual estara representada por la canasta de bienes y servicios que su capacidad de compra le permite adquirir. De este modo, cuando se habla de la función de utilidad se refiere al instrumento para asignar un número a todas las cestas de consumo posibles, de tal forma que las que se seleccionan tengan un valor más alto, que aquellas que se prefieren poco o que no se seleccionan (Varian, 2011). Al asignar un valor a todas las curvas de indiferencia es posible cuantificar y medir los gustos y preferencias del consumidor o inversionista, así como encontrar las reglas de asignación matemática que permitan hallar una función que represente las características propias de dichos agentes (Cohn, Lewellen, Lease & Schlarbaum, 1975).
En estudios realizados por Kallberg y Ziemba (1983), Yu, Pang, Troutt y Hou (2009) y, Cipu y Gheorghe (2015) demostraron que el uso de funciones de utilidad permiten describir y modelar las preferencias de los agentes y de esta forma encontrar su portafolio óptimo. Es evidente entonces, en el contexto de incertidumbre, poder describir cuantitativamente las decisiones que de acuerdo a las preferencias, representen de la mejor manera la elección que se hace frente al riesgo.

Todas estas funciones de utilidad fueron aplicadas por Kahneman y Tversky (1979), Harrison (1986), Viscusi y Evans (1990), Viscusi (1993) y Norstad (1999), quienes no solamente investigaron la función de utilidad que mejor representara el comportamiento de los agentes, sino que también estimaron el riesgo implícito en la toma de decisiones, empleando la EU. En igual forma, estas funciones fueron y son utilizadas en el campo de la macroeconomía, en la teoría del crecimiento y en el mercado de capitales, donde modelan el comportamiento de los agentes en sus decisiones, teniendo como objetivo, por ejemplo, el nivel de consumo de un país, ademas que permiten comparar la tasa de crecimiento respecto a otros países (Rebelo, 1990; Christensen, Jorgenson & Lau, 1975; Xie, 2002).
En muchas ocasiones se habla de incertidumbre y riesgo indistintivamente; sin embargo, son conceptos diferentes y de ahí la importancia de tener clara su definición. La incertidumbre se refiere a hechos que no son posibles de cuantificar o medir, es decir, las probabilidades de ocurrencia son desconocidas y no existe información suficiente. El riesgo, por su parte, corresponde a aquellos hechos que mediante variables aleatorias se pueden medir o conocer su probabilidad. En general, en situaciones de incertidumbre importan las decisiones donde los individuos pueden conocer su probabilidad de ocurrencia (Nicholson, 2005). Knight (2012) argumentó que la incertidumbre y el riesgo son situaciones aleatorias, pero se diferencian fundamentalmente en el desconocimiento de las probabilidades que no son posibles de estimar en condiciones de incertidumbre (Tarapuez, Zapata & Agreda, 2008). La Tabla 1 muestra algunas equivalencias entre estos dos conceptos.
Tabla 1
Equivalencias entre el riesgo e incertidumbre
Riesgo |
Incertidumbre |
Es observable |
No observable |
Existe información para estimarlo |
La data disponible no es precisa |
Estimación objetiva |
Estimación subjetiva |
Incertidumbre de primer grado |
Incertidumbre de segundo grado |
Puede ser estimada estadísticamente |
Es difícil, requiere tiempo y esfuerzo propio |
Fuente: adaptado de Haahtela (2007, p. 5).
La metodologia de toma de decisiones se considera una forma de medir el riesgo desde la conducta de los consumidores; en ella, es de gran importancia no sólo cuantificar la evaluación de los resultados inmersos en el riesgo, sino que tambien, la utilidad que genera dichas elecciones (Dixit & Pindyck, 1994; Rubinfeld & Pindyck, 2013).
Bajo la condición anterior, la EU se convierte un concepto fundamental, porque no sólo permite revelar las preferencias de los agentes, sino asignar un número, es decir, una función de utilidad que la representa. Uno de los primeros autores en conceptualizar sobre EU fue Bernoulli, quien en 1713 planteó la paradoja de San Petersburgo, luego para 1730, demostró que al individuo más que el valor en dinero, es la utilidad la que lo representa (Bernoulli, 1954). Mas tarde, Von Neuman y Morgensten en 1947, desarrollaron la teoría de la EU, teniendo como base los axiomas de la racionalidad de los agentes, para explicar el comportamiento en situaciones de riesgo e incertidumbre, definiendo el riesgo como una lotería, precisando que corresponde a un activo que posee un riesgo de pago, de la cual, el individuo escoge la opción óptima en sentido estocastico, de un conjunto de loterías (Von Neumann & Morgenstern, 2007).
La teoria de Neumann-Morgestern planteó el uso de cuatro axiomas para describir las preferencias de los individuos en sus elecciones bajo incertidumbre, las cuales son: a) la completitud, b) la transitividad, c) la continuidad, y d) la independencia. Mas tarde, Luce y Raiffa (2012) basados en la misma teoria, amplíaron los axiomas a seis, con el objetivo de representar de una mejor manera, las preferencias y el comportamiento racional de un individuo en condiciones de riesgo, estos axiomas se describen a continuacion:
Estos axiomas permiten, en particular el de continuidad, encontrar la función de utilidad que representa el comportamiento del individuo según sean sus preferencias, donde elige y jerarquiza las elecciones teniendo en cuenta su probabilidad, asignando un número que representa la maximización de la EU.

Dadas las características de crecimiento y concavidad de las funciones, y teniendo en cuenta que la aversión absoluta al riesgo decrece con el bienestar; por la existencia de la aversión en las decisiones; que existe evidencia que los individuos no son neutrales al riesgo y mas aún si se presenta continuamente propensión al mismo a largo plazo, se genera quiebra financiera (Maya & Pareja, 2014), bajo un analisis de las funciones anteriormente mencionadas, se descarta la cuadrática, la cubica y la exponencial porque generan aversión al riesgo absoluto creciente y constante respectivamente, la exponencial negativa dado que presenta aversión al riesgo absoluto constante y aversión al riesgo relativo creciente (Pratt, 1964). Lo anterior, permite indicar que la función que modela de manera apropiada el comportamiento de los agentes respecto a su aversión al riesgo, corresponde a la CRRA, debido a que permite diferenciar las preferencias de los agentes deacuerdo con diferentes niveles de concavidad, ademas que asegura retornos de equilibrio y permite la existencia de un crecimiento equilibrado balanceado debido a la su elasticidad intertemporal de sustitucion (Mehra & Prescott, 1985; Suen, 2009)
La estructura de la función de utilidad que se utilizó en esta investigación es:

Multiples son las investigaciones que han utilizado esta función para medir el índice de aversión al riesgo, entre ellas están, Eckel y Grossman (2008), Campo, Guerre, Perrigne y Vuong (2011) y, Harrison, Lau y Rutström (2007). Holt y Laury (2002) en su investigación, encontraron que los agentes son aversos al riesgo y estos se ubicaron en un intervalo entre 0.41 y 0.61, mientras que Harrison, Lau, Rutström y Sullivan (2005), por su parte, obtuvieron que para una población adulta de Dinamarca el coeficiente de aversión al riesgo fue de 0.67. Por su parte, Harrison y Rutström (2008) replicaron los trabajos de Hey y Orme (1994) y el de Holt y Laury (2002), en ellos se utilizaron las metodologías de pareja de loterias aleatorias (random lottery pairs o RLP) y método de diseño de listado de precios multiples (multiple price list design o MPL) respectivamente, pero los resultados indicaron que mientras se estimo un valor de 0.53 para el índice de aversión al riesgo bajo las condiciones del primer trabajo referenciado, al replicar el segundo, el mismo autor estimo un indice de 0.61 bajo la función CRRA; Finalmente Harrison, Johnson, McInnes y Rutström (2003), estimaron el índice de aversión al riesgo, definiendo un intervalo entre -0.5 y 1.25, siendo este ultimo valor, el correspondiente a muy averso al riesgo.
En esta sección se definen el concepto de lotería, seguidamente, se explica el diseño del experimento realizado y al final, se reseñan las investigaciones que sirvieron de base para el desarrollo de este estudio y que justifican la metodología utilizada como elemento comparativo para hallazgos.
Para modelar las elecciones en condiciones de incertidumbre se utiliza el concepto de lotería, definida como:

En la literatura es común encontrar investigaciones, no sólo en el campo económico, que utilizan el juego de loterías como estrategia para medir el comportamiento de un individuo frente a decisiones en situaciones de incertidumbre y riesgo. LaPlante, Gray, Bosworth y Shaffer (2010) publicaron una amplia bibliografía de trabajos realizados en diferentes ciencias. En igual forma, existe una extensa gama de estudios que miden experimentalmente medir el grado de aversión al riesgo y la función de utilidad que lo representa; entre estos estudios, existen dos relevantes para esta investigacion, como son el de Hey y Orme (1994) que recurrieron a un juego binario de lotería utilizando RLP; en su investigación emplearon varias sesiones, cada una de veinticinco preguntas para indagar sobre las generalidades de las preferencias en algunas funciones de utilidad, mientras que Holt y Laury (2002) utilizaron el MPL para medir el grado de aversión al riesgo, utilizando un híbrido de la función de utilidad expo-power mediante incentivos reales e hipotéticos, encontrando que el comportamiento es más errático en los casos hipotéticos en comparación con los reales.
La importancia del experimento planteado radica en poder encontrar evidencia empírica del índice de aversión al riesgo en la función tipo CRRA, elemento clave para investigaciones de toma de decisiones en situaciones de incertidumbre, donde las personas valoran de forma diferente las pérdidas y ganancias en contra de la predicción de la teoría estándar (Brandts, 2009). En el diseño del experimento, de acuerdo a la economía experimental, se hace necesario cumplir con aspectos importantes, Juberías y Cotanda (2004) destacan basados en Smith (1994), como los más significativos los siguientes: el entorno, los recursos iniciales, las preferencias, los costes, las instituciones, el método y las normas como ejes articuladores que mueven el experimento. Atendiendo a lo anterior, en esta investigación en específico, para que el diseño tuviera la suficiente validez y soporte, se hizo necesario que existiera una recompensa para inducir en los sujetos una serie de características importantes, teniendo como objetivo que las particularidades inherentes de los sujetos no fueran relevantes. Smith (1982) propuso las siguientes propiedades para inducir dichas características que deberia cumplir todo experimento: a) monotonicidad, b) prominencia y, c) dominancia. En terminos generales, las anteriores condiciones buscan que el sujeto prefiera más recompensa a menos y que no se preocupe por la recompensa que pueden obtener los demás. Representando lo anterior, de una forma mas estructural, con una función de utilidad dada y unas preferencias inducidas se tiene que:

El experimento de esta investigación cumplió a cabalidad las características presentadas por Juberías y Cotanda (2004) quienes retomaron a Hey (1996); ademas se tuvo en cuenta la estructura general para este tipo de experimentos, que cuenta con tres partes fundamentales: la construcción de la lotería, la encuesta demográfica y el experimento en sí. Las loterías seleccionadas fueron dos de tipo simples, la Tabla 2 muestra las probabilidades utilizadas en las 25 preguntas que se estimaron, donde PD corresponde a las probabilidades de la lotería de la derecha y PI a las de la izquierda.
Tabla 2
Probabilidades asignadas a cada pregunta del experimento

Fuente: elaborada por el autor con base en Holt y Laury (2002) y, Hey y Orme (1994).

Para la realización del experimento se utilizaron dos grupos con el fin de comparar similitudes y diferencias entre ellos, ambos de pertenecientes a Finanzas de la Universidad EAFIT, el primero de ellos de la especialización de la sede en Bogotá y el segundo a nivel de pregrado en la sede en Medellín, con la participación de 21 y 20 estudiantes respectivamente. Se utilizaron computadores portátiles donde los participantes realizaron la encuesta, la cual habia sido enviada minutos antes a los respectivos correos electrónicos, mediante un link que los direccionaba a la encuesta y a las instrucciones; en tal sentido la plataforma que se utilizó para todo este procedimiento fue Qualtrics.
El experimento se dividio en dos partes o momentos, el primero de ellos consistió en completar la encuesta demográfica con los datos solicitados y luego una segunda etapa, el sujeto de prueba debia decidir y elegir, entre dos alternativas en cada una de 25 pares de loterías con premios fijos de 0.3, 0.6 y 1. La Figura 1 muestra el ejemplo que se suministró a los estudiantes en las instrucciones, antes que procedieran a realizar las escogencias.
Figura 1
Ejemplo entregado a los estudiantes

En este ejemplo, si se elige la opción A puede ganar una bonificación de 0.6 con una probabilidad de 30% o una bonificación de 0.30 con probabilidad de 30% o finalmente, 1 con una probabilidad de 40%. Si elige la opción B podrá ganar una bonificación de 1 con una probabilidad de 20%, una bonificación de 0.3 con probabilidad de 40% o 0.6 con una probabilidad de 40%.
Dada las limitantes de tiempo y de restricción presupuestaria para la ejecucion del experimento se hace necesario indicar que se presentaron los siguientes inconvenientes: el primero de ellos estaba en función del espacio y del tiempo, pues no fue posible realizarlo con más de treinta personas pues la disponibilidad de tiempo de los estudiantes era bastante limitada y dependía exclusivamente de su interés real de participar en el experimento y de conocer de forma individual cual era su nivel de aversion frente al riesgo; en segundo lugar, no se contaba con los suficientes recursos económicos para realizar a cabalidad el experimento, por lo cual se optó por encontrar otro tipo de incentivo como obtener una bonificación extra en la nota final de determinada materia, lo cual permitió no afectar las condiciones del experimento, y lo más importante, que la recompensa se considerara motivadora para los participantes e indujera a las características preestablecidas. En tal sentido, la literatura argumenta a traves de Read (2005), que el incentivo en dinero no es ni suficiente ni necesario para lograr los objetivos de una investigación; mientras que resultados obtenidos por Melo (1993) indicaron que en diversos experimentos desarrollados sin incentivos económicos se encontraron resultados útiles y apropiados, en donde a pesar de que los valores generales en cada experimento fueron diferentes, las conclusiones se conservaron.
Finalmente, para la realización de este experimento se tuvieron en cuenta las condiciones y procedimientos planteados en los trabajos tradicionales en temas de economia experimental, como los de Harrison, Martínez-Correa y Swarthout (2014) quienes utilizaron diferentes juegos de loterías para medir la aversión al riesgo para la función CRRA, mientras que los trabajos de Harrison y Rutström (2008) y, Harrison y Rutström (2009) sirvieron como elemento guía y base fundamental para la metodología, gracias a su facilidad en la comprensión para los participantes del experimento y como replica de sus trabajos.
En esta sección se describe la estructura y el proceso para estimar el parámetro que subyace en la funcion tipo CRRA y que permite modelar el comportamiento o preferencias de un agente economico.

Como parámetros se utilizan los valores dados en la Tabla 3.
Tabla 3
Coeficiente de aversión al riesgo en la
funcion CRRA y su respectiva definición

Fuente: Aliaga Lordemann, J. & Oropeza, A. (2015)
en base a Holt y Laury (2002)
Los calculos y resultados de la presente investigacion se estimaron utilizando en el software Stata. Para el experimento realizado con el grupo de Bogotá, el índice medio de aversión al riesgo estimado fue de A = 0.56, lo que significa que los integrantes de este grupo son aversos al riesgo. Ahora bien, los resultados del grupo de la Sede Medellín, arrojaron un índice medio de aversión al riesgo estimado de A=0.68, lo que implica que se encuentra en el intervalo de muy averso al riesgo, pero es de notar que ambos, como lo estima la teoría, son aversos frente riesgo y que la diferencia entre medias, se estima no estadisticamente significativa (véase Tabla 4 y 5).
Tabla 4
Estimación del parámetro para el grupo de estudiantes de Bogotá

-----
Tabla 5
Índice de aversión al riesgo, estudiantes del grupo de Medellín

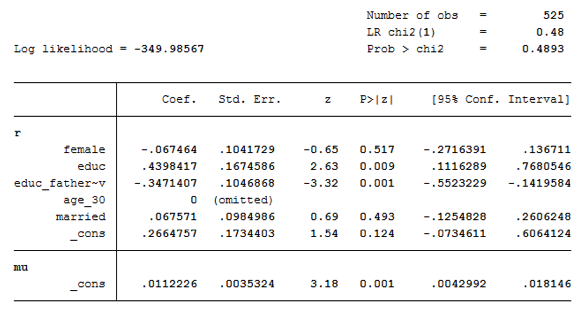
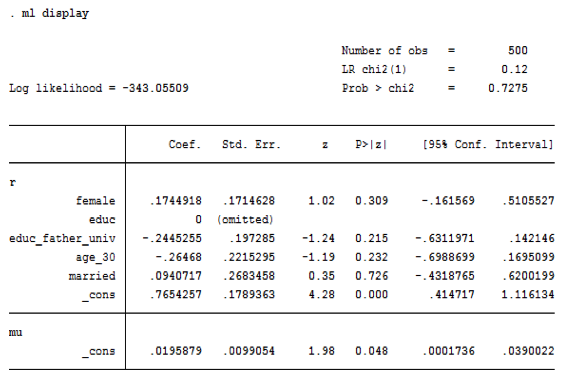
Con respecto a los resultados obtenidos al incluir en la estimación las variables demográficas en el grupo de Bogotá (ver Tabla 6), se encontro que las variables significativas con un nivel de confiabilidad de 95% son educ, que equivale a la educación del estudiante, y educ_father~v que representa la educación del padre con un p-value de 0.009 y 0.001 respectivamente. Adicionalmente, en la variable educación del estudiante, referida a si este poseia un titulo de especialización, se observo que los individuos que cumplian don dicha caracteristica eran menos aversos, con un coeficiente cercano a 0.43, en comparación al grupo en general. En lo que se refiere al grupo de Medellín (véase Tabla 7), no se observaron efectos significativos en ninguna de las variables medidas con un nivel de confiabilidad del 95%. Asimismo, para una muestra pequeña, como en este caso, las variables demográficas no afectan la decisión de los individuos frente a su aversión al riesgo, como lo refieren los trabajos de la misma línea y que fueron referenciandos anteriormente.
Tabla 6
Coeficientes de las variables demográficas para el grupo de Bogotá
-----
Tabla 7
Coeficientes de las variables demográficas para el grupo de Medellín.
------

Al revisar la función de densidad por género, en las figuras 2a y 2b, y basados en la Tabla 3, se encontró que en el grupo perteneciente a la ciudad de Bogotá, los hombres son más aversos al riesgo que las mujeres, sin desconocer que algunos de ellos se ubicaron en el nivel de ligeramente aversos, lo cual se observa en la gráfica de la curva de línea continua. En el grupo de Medellín, por el contrario, las mujeres resultaron más aversas al riesgo que los hombres, lo anterior indica, y como lo soporta la tabla de variables demográficas, que no existe diferencia en la aversión por genero.
Con respecto a la función de aversión al riesgo, la curva cóncava estimada confirma que ambos grupos son aversos al riesgo, tal y como lo plantea la teoria, resultado que se refleja en las figuras 3a y 3b:
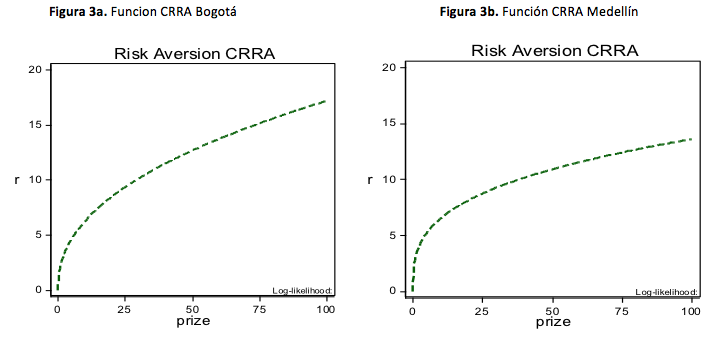
Finalmente, se confirmo que a la luz de los resultados, que ambos grupos arrojaron un índice de aversión al riesgo parecido, el cual indicó presencia de aversión al riesgo, sin embargo, al ver la distribución de los datos, presentados en la Figura 4, fue posible identificar que existe asimetría en la distribución de cada uno de ellos; en el grupo de Bogotá los valores de la CRRA se ubicaron, en su mayoría, por debajo de 0.4 y por encima de 0.6; en cambio, en el grupo de Medellín los valores de la CRRA mostraron valores más cercanos a la media encontrada, obviamente lo anterior debido al tamano de la muestra utilizada.

El presente articulo propuso el uso de la metodologia EU y de función de utilidad para la evaluacion del coeficiente de aversión al riesgo que se estimó para la funcion tipo CRRA, la cual se empleó debido al comportamiento de los agentes respecto a su aversión frente al riesgo, además de que cumple con una serie de características importantes como son la aversión absoluta al riesgo decreciente y la posibilidad de diferenciar las preferencias de los agentes a partir de distintos niveles de concavidad, mostrando que los individuos no son neutrales al riesgo.
La investigación permitió evaluar las decisiones de los individuos en las que se involucra el factor riesgo con base en la teoría de la EU; en este orden de ideas, nuestro principal aporte fue que se logró estimar el grado de aversión mediante el coeficiente Gamma que subyace en la función tipo CRRA, utilizando para ello un experimento con dos grupos de individuos bajo diferentes contextos; en él se da cuenta del comportamiento de los individuos en la toma de decisiones bajo riesgo e incertidumbre, lo cual está a la par de lo que plantea la teoría económica.
Para la implementacion de la metodología se apropiaron una serie de técnicas, que incluyeron el juego de loterías bajo dos métodos RLP y MPL; vale la pena resaltar que su utilización resulta simple y fácil de implementar con todo tipo de individuos y permite encontrar resultados óptimos y coherentes.
En cuanto a los resultados del experimento, se logró calibrar y estimar a cabalidad el coeficiente de aversión al riesgo, donde la media para ambos grupos es similar y su diferencia no es estadisticamente significativa; con respecto a las variables demográficas se encontró que la edad, el ingreso y el género se presentaron como no significativas, es decir, las condiciones particulares del experimento no influyen sobre las elecciones de los individuos. En función de lo anteriormente mencionado vale la pena indicar que las muestras fueron pequeñas, lo que no permite llegar a una conclusión para su uso generalizado, pero que permitió alcanzar resultados positivos y satisfactorios.
Finalmente, se exhorta que para futuras investigaciones se puedan utilizar otros tipos de funciones para fines comparativos, como puede ser el uso de la función expo-power, la cual exhibe características similares para medir la aversión al riesgo, además de su importante condición de flexibilidad para modelar cualquier tipo de agente. Ademas tambien se considera importante, ampliar la base de individuos sobre los cuales se hacen este tipo de experimentos con el fin de encontrar unos resultados que se puedan generalizar.
Alchian, A. A. (1953). The Meaning of utility measurement. The American Economic Review, 43(1), 26-50.
Aliaga J. & Oropeza, A. (2015). Análisis experimental de la Curva de Laffer y la evasión fiscal en Bolivia. Revista Latinoamericana de Desarrollo Económico, (24), 121-153.
Beedles, W. L. (1978). On the use of certainty equivalent factors as risk proxies. Journal of Financial Research, 1(1), 15-21.
Bernoulli, D. (1954). Exposition of a new theory on the measurement of risk. Econométrica: Journal of the Econometric Society, 22, 23-36.
Brandts, J. (2009). La economía experimental y la economía del comportamiento. En J. C. García-Bermejo (ed.), Sobre la economía y sus métodos (pp. 125- 142). Madrid: Trotta.
Campo, S., Guerre, E., Perrigne, I. & Vuong, Q. (2011). Semiparametric estimation of first-price auctions with risk-averse bidders. The Review of Economic Studies, 78(1), 112-147.
Capinski, M. J., Kopp, E. & Ski, M. J. C. (2014). Portfolio theory and risk management. Cambridge, Reino Unido: Cambridge University Press.
Christensen, L. R., Jorgenson, D. W. & Lau, L. J. (1975). Transcendental logarithmic utility functions. The American Economic Review, 65(3), 367-383.
Cipu, C. & Gheorghe, C. (2015). Some applications in economy for utility functions involving risk theory. Procedia Economics and Finance, 22, 595-600.
Cohn, R. A., Lewellen, W. G., Lease, R. C.& Schlarbaum, G. G. (1975). Individual investor risk aversion and investment portfolio composition. The Journal of Finance, 30(2), 605-620.
Dixit, A. K. & Pindyck, R. S. (1994). Investment under uncertainty. Princeton, Estados Unidos: Princeton University Press.
Eckel, C. C. & Grossman, P. J. (2008). Forecasting risk attitudes: An experimental study using actual and forecast gamble choices. Journal of Economic Behavior & Organization, 68(1),1-17.
Haahtela, T. (2007). Separating ambiguity and volatility in cash flow simulation based volatility estimation. Recuperado de http:// papers.ssrn.com/sol3/papers.cfm?abstractid=968226
Harrison, G. W. (1986). An experimental test for risk aversion. Economics Letters, 21(1), 7-11.
Harrison, G. W., Johnson, E., McInnes, M. M. & Rutström, E. E. (2003). Individual choice and risk aversion in the laboratory: A reconsideration. Department of Economics Working Paper, 3-18.
Harrison, G. W., Lau, M. I. & Rutström, E. E. (2007). Estimating risk attitudes in denmark: A field experiment. The Scandinavian Journal of Economics, 109(2), 341-368.
Harrison, G. W., Lau, M. I., Rutström, E. E. & Sullivan, M. B. (2005). Eliciting risk and time preferences using field experiments: Some methodological issues. Field Experiments in Economics, 10, 125-218.
Harrison, G. W., Martínez-Correa, J. & Swarthout, J. T. (2014). Eliciting subjective probabilities with binary lotteries. Journal of Economic Behavior & Organization, 101, 128-140.
Harrison, G. W. & Rutström, E. E. (2008). Risk aversion in the laboratory. En J. C. Cox & G. W. Harrison (eds.), Risk Aversion in Experiments. Bingley, Reino Unido: Emerald, Research in Experimental Economics.
Harrison, G. W. & Rutström, E. E. (2009). Expected utility theory and prospect theory: One wedding and a decent funeral. Experimental Economics, 12(2), 133-158.
Hey, J. D. (1996). Experimentos en economía. México D. F., México: Fondo de Cultura Económica.
Hey, J. D. & Orme, C. (1994). Investigating generalizations of expected utility theory using experimental data. Econometrica: Journal of the Econometric Society, 1291-1326.
Holt, C. A. & Laury, S. K. (2002). Risk aversion and incentive effects. American Economic Review, 92(5), 1644-1655.
Juberías, E. F. & Cotanda, J. M. R. (2004). Una introducción a la metodología experimental en economía. Cuadernos de Economía: Spanish Journal of Economics and Finance, 27(75), 7-36.
Kahneman, D. & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica: Journal of the Econometric Society, 47(2), 263-291.
Kallberg, J. G. & Ziemba, W. T. (1983). Comparison of alternative utility functions in portfolio selection problems. Management Science, 29(11), 1257-1276.
Knight, F. H. (2012). Risk, Uncertainty and Profit. Massachusetts, Estados Unidos: Courier Corporation.
LaPlante, D. A., Gray, H. M., Bosworth, L. & Shaffer, H. J. (2010). Thirty years of lottery public health research: Methodological strategies and trends. Journal of Gambling Studies, 26(2), 301-329.
Luce, R. D. & Raiffa, H. (2012). Games and Decisions: Introduction and Critical Survey. Massachusetts, Estados Unidos: Courier Corporation.
Maya, C. & Pareja, J. (2014). Valoración de opciones reales a través de equivalentes de certeza. Revista Ecos de Economía, 18(39), 49-72.
Mehra, R., & Prescott, E. (1985). The equity premium: A puzzle. Journal of monetary Economics, 15(2), 145-161.
Melo, L. (1993). Los incentivos monetarios en la economía experimental: Un estudio de caso. Desarrollo y Sociedad, 31, 9-120.
Meyer, D. J. & Meyer, J. (2005). Relative risk aversion: What do we know?. Journal of Risk and Uncertainty, 31(3), 243-262.
Nicholson, W. (2005). Teoría microeconómica: principios básicos y ampliaciones. Madrid, España: Ediciones Paraninfo.
Norstad, J. (1999). An introduction to utility theory. Recuperado de http://homepage. mac. com/j. norstad
Pareja, J. & Cadavid, C. (2016). Valoración de patentes farmacéuticas a través de opciones reales: equivalentes de certeza y función de utilidad. Contaduría y Administración, 61(4), 794-814.
Pratt, J. W. (1964). Risk aversion in the small and in the large. Econometrica: Journal of the Econometric Society, 32(1/2), 122-136.
Rebelo, S. T. (1990). Long run policy analysis and long run growth. Technical Report, National Bureau of Economic Research, s.d.
Read, D. (2005). Monetary incentives, what are they good for?. Journal of Economic Methodology, 12(2), 265-276.
Rubinfeld, D. & Pindyck, R. (2013). Microeconomics. Nueva Jersey, Estados Unidos: Pearson Education.
Smith, V. L. (1982). Microeconomic systems as an experimental science. The American Economic Review, 72(5), 923-955.
Smith, V. L. (1994). Economics in the laboratory. The Journal of Economic Perspectives, 8(1), 113-131.
Suen, R. (2009). Bounding the CRRA utility functions.
Tarapuez, E., Zapata, J. A. & Agreda, E. (2008). Knight y sus aportes a la teoría del emprendedor. Estudios Gerenciales, 24(106), 83-98.
Varian, H. R. (2011). Ejercicios de microeconomía intermedia. Barcelona, España: Antoni Bosch.
Viscusi, W. K. (1993). The value of risks to life and health. Journal of Economic Literature, 31(4), 1912-1946.
Viscusi, W. K. & Evans, W. N. (1990). Utility functions that depend on health status: estimates and economic implications. The American Economic Review, 353-374.
Von Neumann, J. & Morgenstern, O. (2007). Theory of Games and Economic Behavior, Estados Unidos: Princeton University Press.
Xie, D. (2002). Power risk aversion utility functions. International Finance.
Yu, B. W. T., Pang, W. K., Troutt, M. D. & Hou, S. H. (2009). Objective comparisons of the optimal portfolios corresponding to different utility functions. European Journal of Operational Research, 199(2), 604-610.

1. PhD (c) en Administración Estratégica de Empresas de Centrum Católica de Perú, Profesor Asociado de Finanzas de la Universidad EAFIT, adscrito a la Escuela de Economía y Finanzas. Correo electrónico: jparejav@eafit.edu.co
2. Licenciado en Matemáticas y Física, Universidad de Antioquia. Correo electrónico: mailto:jbaenaa@eafit.edu.co