ISSN 0798 1015

Vol. 38 (Nº 30) Año 2017. Pág. 8

Ensino da matemática financeira para alunos do 8º e 9º ano do ensino fundamental: uma proposta na perspectiva da educação matemática crítica

The teaching of financial math to students in the 8th and 9th grade from the elementar school: A proposal in the perspective of the critical mathematical education.

Soliane MOREIRA 1; Juliana de Fatima Holm BRIM 2; Nilcéia Aparecida Maciel PINHEIRO 3; Sani de Carvalho Rutz DA SILVA 4

Recibido: 25/02/2017 • Aprobado: 08/03/2017

Conteúdo

1. Introdução

2. Educação matemática crítica e matemática financeira

3. A proposta

4. Considerações finais

Referências bibliográficas

1. Introdução

A área de pesquisa da Educação Matemática recebe contribuições de novas perspectivas teóricas que tratam de diferentes olhares relacionados às questões de ensino e aprendizagem. Inúmeras pesquisas, como dos autores Skovsmose(2000,2001), D’Ambrosio(2000, 2005), Borba(2004), Moura(2012), Lenzi(2008), Frederico(2014), Biembengut(2009), vêm tratando sobre novas metodologias para o ensino cuja finalidade é dar significado aos conhecimentos, procurando associar conhecimentos científicos com conhecimentos práticos.  Além disso, existem outros estudos que apontam quais e como abordar os conhecimentos matemáticos em sala de aula, importantes e necessários aos alunos para que atuem de forma critica na sociedade.

Este trabalho traz uma proposta para se trabalhar um conteúdo em sala de aula abordando as duas perspectivas mencionadas acima. Para isso, usou-se a abordagem da Educação Matemática Crítica no ensino da Matemática Financeira, buscando assim conexões entre aspectos teóricos e práticos no desenvolvimento de uma postura investigativa, reflexiva e crítica do aluno. Pois vive-se em uma sociedade globalizada, que é caracterizada pelo acúmulo de informações e pela necessidade de tomada de decisões em situações de incerteza.

A opção pela Matemática Financeira fundamenta-se pela sua abordagem a temas da realidade, vastamente contemplados pela mídia e que requerem atenção especial, conforme possibilitam avaliar e resolver situações relacionadas no dia a dia.

O objetivo deste trabalho além da elaboração de uma proposta metodológica para se trabalhar o ensino da matemática financeira na perspectiva da Educação Matemática Crítica, é também com isso auxiliar professores a desenvolver suas aulas de forma significativa para os alunos. Para isso, apresentamos a seguir uma discussão sobre as teorias abordadas nesse artigo.

2. Educação matemática crítica e matemática financeira

Os objetivos dos PCN de Matemática do Ensino Fundamental indicam que os alunos devem ser capazes de: “questionar a realidade formulando-se problemas e tratando de resolvê-los, utilizando para isso o pensamento lógico, a criatividade, a intuição, a capacidade de análise crítica, selecionando procedimentos e verificando sua adequação”(BRASIL, 1998 p. 8). Muitos podem dizer ou pensar que a matemática não tem responsabilidade sobre isso, que o ensino da matemática se reduz aos conteúdos escolares e listas de exercícios. E para contrariar ainda mais a visão tradicionalista do ensino, outro objetivo é “saber utilizar diferentes fontes de informação e recursos tecnológicos para adquirir e construir conhecimentos”(BRASIL, 1998 p. 8). Esses objetivos perpassam sobre o papel da matemática na sociedade. E também como deve ser o comportamento dos estudantes, pensando na postura deles em relação aos problemas sociais.

Não se pode pensar nos objetivos acima mencionados desvinculados do propósito de dar sentido aos conhecimentos matemáticos. Nessa perspectiva, no que tange a educação matemática, o aluno deve ser um sujeito crítico e reflexivo, que é um dos pressupostos da Educação Matemática Crítica.

Passos (2008, p. 42) declara que “um dos mais importantes objetivos da Educação Matemática Crítica é o desenvolvimento de novas atitudes com relação aos papéis realizados pelos conhecimentos matemáticos na sociedade”.

Dentro desse contexto, as pessoas que não dispõe do conhecimento matemático, apresentariam muitas dificuldades em julgar as decisões que estão sendo tomadas, e de sustentar uma maneira crítica em meio a um ambiente em que a matemática está presente. Dessa maneira, a alfabetização matemática tem uma função extremamente significativa na formação de cidadãos atuantes e no desenvolvimento da competência democrática destes cidadãos, bem como o conhecimento tecnológico e o conhecer reflexivo.

Na perspectiva da Educação Matemática Crítica (EMC), o ensino da matemática deve ter significado para o aluno, necessita direcioná-lo a fazer uma reflexão crítica da realidade social que está incluído, acarreta educar de maneira democrática, permitindo que todos envolvam-se ativamente, como sujeitos, na sociedade. Nas obras de Skovsmose (2008), esta se caracteriza como uma das principais inquietações em suas reflexões acerca do tema: a Educação Matemática não se reduz à técnica de ensinar matemática, entretanto se configura como uma ação de educar matematicamente para a vida.

Diante dos desafios que configuram o ensino de matemática hoje nas escolas, os PCN indicam que a matemática deve ser trabalhada de forma a suscitar o desenvolvimento e a obtenção de competências e habilidades imprescindíveis para que o aluno, como cidadão, venha associar-se à sociedade, transformando e aperfeiçoando a realidade social. (BRASIL, 1999b). Pressupõe-se sair do ensino tradicional para novas metodologias e estratégias para o ensino da matemática.

O mesmo autor classifica de tradicional, as práticas baseadas na resolução de exercícios estruturados como uma série de ordens: resolva, efetue, calcule, etc, essas atividades são descontextualizadas e o material didático é pouco variado. Ressalta ainda, que a estimava de que, em sua vida escolar, os alunos do ensino fundamental ao ensino médio, são expostos a aproximadamente 10.000 exercícios, na sua maioria, baseados em comandos (SKOVSMOSE, 2007).

Skovsmose (2001, 2008) fez uma diferenciação entre dois tipos de organização das aulas de matemática que são o paradigma o exercício, ensino tradicional, e os cenários para investigação. Em outro texto, apresenta uma proposta de exploração matemática e justificação, feita pelos estudantes, cujo objetivo principal é o de criar uma contraposição ao que ele denomina paradigma do exercício (SKOVSMOSE, 2000), as diferenças são mostradas suscintamente na quadro 1.

Quadro 1 – Exercícios x cenários de investigação 1

Fonte: Skovsmose (2001, 2008)

Com relação às atividades,

Um cenário para investigação é aquele que convida os alunos a formularem questões e procurarem explicações. O convite é simbolizado pelo “O que acontece se...?” do professor. O aceite dos alunos ao convite é simbolizado por seus “Sim, o que acontece se...?”. Dessa forma, os alunos se envolvem no processo de exploração. O “Por que isto...?” do professor representa um desafio e os “Sim, por que isto...?” dos alunos indicam que eles estão encarando o desafio e que estão procurando por explicações. (SKOVSMOSE, 2000, p. 73).

A finalidade de Skovsmose (2000), ao apresentar os cenários para investigação, correlaciona-se com a Educação Matemática Crítica, que se importa, dentre outras coisas, com o desenvolvimento da materacia, ideia também discutida por D’Ambrosio (1999). Materacia não se trata somente das habilidades matemáticas, assim como da competência de interpretar e atuar numa circunstância social e política estruturada pela matemática. (SKOVSMOSE, 2000, p. 68).

A partir das ideias já mencionadas sobre o paradigma do exercício x cenários de investigação, Skovsmose (2000) diferencia seis modelos que advém da combinação das referências: matemática pura; semi-realidade; realidade, cujo objetivo é fazer com que os alunos elaborem significados para os conceitos e as atividades.

A quadro 2 a seguir mostra de forma resumida as seis possibilidades apresentadas por Skovsmose.

Quadro 2 - Exercício x cenários de investigação

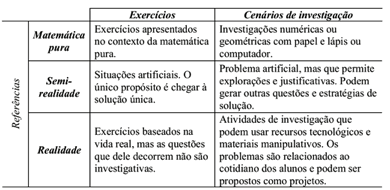
Fonte: Skovsmose (2001, 2008)

Diante do exposto acima, na quadro 2, espera-se que o professor prepare suas aulas com o objetivo que seus alunos desenvolvam suas capacidades e que estas, propiciam intervir na realidade a fim de transformá-la. Para isso, o dialogo deve ser um elemento essencial em sala de aula, podendo assim nas discussões abranger os problemas do cotidiano e para que tomem consciência dos aspectos sociais, que muitas vezes passam despercebidos por eles. Assim transformando reflexão em ação e nesse sentido utiliza-se das contextualizações para abordar diversos conteúdos, dentre eles a Matemática Financeira.

E ensinar esse conteúdo na perspectiva da EMC é explorar uma Matemática Financeira que desenvolva competências, que os estudantes se tornem mais participativos e críticos no modo como esses conhecimentos realizam-se em suas vidas. Como exemplo pode-se citar os PCN:

Para compreender, avaliar e decidir sobre algumas situações da vida cotidiana, como qual a melhor forma de pagar uma compra, de escolher um financiamento etc. é necessário trabalhar situações-problema sobre a Matemática Comercial e Financeira, como calcular juros simples e compostos e dividir em partes proporcionais pois os conteúdos necessários para resolver essas situações já estão incorporados nos blocos.(BRASIL, 1998 p. 86)

Diante desta reflexão apresenta-se a seguir uma proposta de ensino da matemática financeira na perspectiva da EMC para alunos do 9º ano do ensino fundamental.

3. A proposta

A matemática financeira está presente no cotidiano de todas as pessoas. Em diversas situações do dia a dia é possível encontrar problemas envolvendo tomadas de decisões à respeito das melhores taxas de juros, formas de pagamento, empréstimos financiamentos e etc. Algo tão presente nas vidas dos cidadãos, ainda é pouco tratado dentro das salas de aula.

Os livros didáticos, quando trazem a matemática financeira, a tratam superficialmente sem relaciona-la com a realidade da maioria dos estudantes. Esse conteúdo acaba sendo transmitido sem o desenvolvimento crítico dos alunos, o que os levaria a serem futuros cidadãos a tomarem decisões corretas no mercado financeiro e também ao consumo consciente. Alguns professores priorizam conteúdos, que por eles são considerados mais importantes, como equações, logaritmos, médias e acabam perdendo a oportunidade de trabalha-los em problemas básicos da matemática financeira. Conforme Sá (2011 p. 68)

Muitas vezes, em nossas aulas de  matemática, ensinamos aos alunos do ensino médio o que são progressões, mostramos as fórmulas, resolvemos exercícios de aplicação e, normalmente, não aproveitamos a oportunidade para trabalhar o conceito de juro, bem como suas aplicações em situações de empréstimos ou investimentos.

Trabalhar a matemática financeira abordando situações do cotidiano, gerando simulações em relação ao mercado financeiro é uma ótima maneira de tornar as aulas atrativas e proveitosas sem deixar os conteúdos importantes de lado.  Os parâmetros curriculares enfatizam que se deve procurar relacionar os conteúdos ministrados com o dia a dia das pessoas. Além disso, o professor ao levar tais questões para sala de aula, permitindo a participação crítica dos alunos, estará também contribuindo para a formação de cidadãos ativos e pensantes na sociedade. A matemática financeira e comercial é fundamental no processo de constituição de cidadãos críticos (D’Ambrosio 2002), ter o conhecimento financeiro possibilita compreender situações, intervir e tomar decisões.

Ao relacionar a matemática financeira ao cotidiano do aluno faz-se necessário pensar qual o tipo de problema seria o ideal para a turma em que se pretende trabalhar, levando em consideração a faixa etária desses alunos e quais produtos comerciais os interessam. Trazer exercícios, que não apresentam sentido algum aos alunos é característica do ensino tradicional da matemática o qual conforme Skovsmose (2015) não ajuda a desenvolver a criatividade matemática e pode fazer com que se preserve uma visão equivocada da sociedade. A educação matemática critica tem uma abordagem investigativa, os problemas trazidos devem ser um convite aos alunos a formularem questões e procurarem explicações que o levem as possíveis soluções.

Uma tendência matemática pertinente à abordagem da matemática financeira na perspectiva da educação matemática critica é a resolução de problemas. Na tendência matemática de resolução de problemas, os problemas são abertos, muitas vezes provenientes de situações reais, que levam os alunos a refletir, despertando a criatividade, invenção e iniciativa. Conforme Silveira e Miola (2008) trabalhar com essa tendência requer a seleção de problemas que realmente exigem dos alunos alguma habilidade na busca de estratégias de solução e as operações matemáticas ocorrerão por necessidade na busca pela solução apropriada.

Na sequencia é apresentada uma proposta que pode ser trabalhada conciliando a matemática financeira com situações do cotidiano. A atividade utiliza a tendência resolução de problemas no contexto da Educação Matemática Crítica.

3.1 Atividade 1

Público alvo: 9º ano, ensino fundamental.

No comércio é comum encontrar várias propagandas anunciando os mais diversos tipos de produtos e formas de pagamento. Muitas vezes as propagandas mostram valores atrativos ao anunciar um produto sendo vendido à prazo, porém não mostram o valor do juro embutido nas prestações. A área da matemática financeira que trabalha com os juros inseridos nas parcelas em compras à prazo ou financiamentos é denominada “amortizações compostas” que geralmente é trabalhada no ensino médio porem é possível introduzir esse conteúdo  no 9º ano do ensino fundamental desde que o número máximo de prestações seja dois.

É possível também abordar o sistema Price, que trabalha com parcelas fixas e os juros embutidos, bem como as parcelas que são compostas de amortização e juros. A escolha do tema do problema é voltada para a aquisição de celulares, objeto tecnológico que atualmente faz parte do cotidiano dos alunos nessa faixa etária. Segue o problema elaborado para a proposta:

Uma loja de aparelhos celulares apresenta as seguintes condições de pagamento:

Figura 1 – Anuncio: venda de celular
Fonte: Elaborada pelas autoras

Qual a taxa de juro sobre o saldo devedor esta sendo cobrado pela loja?

Ao analisar o problema e buscar a solução o aluno tem a tendência em resolvê-lo da seguinte maneira:

Preço à prazo 2 x de R$ 490,00 o que resulta em R$980, como o preço à vista é R$950,00,  fazendo a diferença entre R$980,00 e R$950,00, obtém-se R$ 30,00 que seria o total de juros pago. Calculando a porcentagem à partir da divisão de R$30,00 por R$ 950,00, obtém-se aproximadamente 0,0315 que corresponde a taxa de juros de 3,15% ao mês.

Porém a solução acima esta incorreta. O erro aparece ao somar valores que estão em datas diferentes. Neste momento o professor pode mostrar aos alunos como funciona o sistema de amortizações compostas, o chamado “juros sobre juros”, que no contexto brasileiro na grande maioria das negociações financeiras é o que impera. Dentro do sistema de amortizações compostas solução correta, esperada seria:

Na compra a prazo, considerando  i a taxa de juros, em um primeiro momento ao sair da loja, sem realizar nenhum pagamento deve-se:

950 + 950.i = 950 (1 +  i)

 ( 1 + i ) é o fator de acréscimo, que nesse sistema aparecerá em todas as parcelas. Chamando (1 + i) de F, em um segundo momento, ao realizar o primeiro pagamento tem-se a seguinte situação:

950.F – 490

Deve-se ainda:

(950.F – 490).F

Em um terceiro momento ao realizar o segundo e ultimo pagamento tem-se a seguinte situação:

(950.F – 490).F – 490 = 0

950.F² – 490.F – 490= 0

Resolvendo a equação do segundo grau e desconsiderando a raiz negativa, obtemos F é aproximadamente 1,0209 o que corresponde a taxa de juros de 2,09% ao mês.

Na sequência da atividade os alunos poderão construir juntamente com o professor a tabela Price que mostra como é dada a composição das parcelas em relação a amortização e juro:

Tabela 1 – Composição das parcelas: juro e amortização

Fonte: Elaborada pelas autoras

Mostrar aos alunos que a diferença em centavos dada na última linha da tabela 1 é devido ao arredondamento da taxa de juros para facilitar os cálculos.

Espera-se com a proposta trazer problemas do cotidiano do aluno para a sala de aula promover cenários de investigação que proporcione momentos de reflexão em relação as melhores formas de pagamento, juros, sistema de amortização e que auxiliem os alunos a entenderem o sistema financeiro ao qual estão inseridos.

3.2 Atividade 2

Público alvo: 8º ano ensino fundamental.

Nessa segunda atividade, o objetivo geral é mostrar aos alunos qual é o juro cobrado e de que forma os cálculos são efetuados nos produtos que são vendidos à prazo, ou que pedem uma entrada e parcelam o restante. Muitas vezes as propostas de vendas das lojas em geral são tentadoras, pois apresentam formas de pagamento acessíveis, porém, basta refletir um pouco na proposta e o consumidor irá verificar que o juro é exorbitante, isso é bem comum, principalmente em financiamentos de bens com altos valores aquisitivos como automóveis e imóveis.

A atividade a seguir é simples, pois trabalha com produto de valor aquisitivo razoavelmente baixo, para melhor entendimento por parte dos alunos, considerando que estes  estão no 8º ano, mas é válida pois promove uma simulação de compra e venda, onde através desse cenário de investigação, eles estarão refletindo e aprendendo a ter consciência ao   adquirir um bem futuramente, seja de qual for o valor. A finalidade dessa atividade é despertar nos alunos futuros consumidores conscientes e sábios em tomar suas decisões financeiras além de mostrar os conceitos matemáticos em situações do cotidiano das pessoas. No 8º ano, os alunos já se apropriaram do conteúdo porcentagem, porém ainda não aprenderam resolver equações do segundo grau, sendo esse conteúdo programado para o 9º ano, portanto a atividade se restringe a apenas uma prestação.

O cenário de investigação apresentado é dado através do seguinte anuncio de venda da figura 2, a seguir, a escolha do produto deve ser de acordo com o interesse da faixa etária dos alunos do 8º ano. Para que se torne um cenário de investigação atrativo é necessário, criar um anuncio com ilustração impresso para ser entregue aos alunos.

Uma loja de aparelhos eletrônicos anuncia a venda de um fone de ouvido, com duas possibilidades de pagamento:

Figura 2 – Anuncio: venda de fone de ouvido
Fonte: Elaborada pelo autor

Com intuito de promover a reflexão sobre o anuncio da figura 2, lança-se a seguinte questão aos alunos: Quanto você pagaria de juros se adquirisse o produto utilizando a segunda opção de pagamento?

Para provocar a reflexão sobre a questão apresentada o professor pode mostrar a solução que a maioria das pessoas que desconhecem cálculos financeiros daria:

30% de R$ 250,00 é igual a R$ 75,00 então 250,00 – 75,00 = 175,00, ou seja, após a entrada de 30% o saldo devedor seria R$ 175,00, como o anuncio diz que seria R$ 190,00 para 30 dias, fazendo a subtração 190,00 – 175,00 = 15,00,  sendo assim R$ 15,00 de juro, sendo que a taxa do juro cobrado poderia ser obtida pelo calculo 15: 250 = 6%.

A proposta é que o professor deixe, por alguns minutos, que os alunos reflitam sobre a solução apresentada deixando-os livres para concordarem ou discordarem, após esse momento de reflexão, o professor, como mediador do conhecimento, irá mostrar a maneira correta de se resolver à questão proposta:

Ao pagar a entrada de 30%, que seria R$ 75,00, o comprador assume uma divida de  R$ 175,00, e é sobre esse valor, que é denominado saldo devedor, que os cálculos devem ser realizados. Os juros cobrados devem ser calculados considerando o aumento R$ 175,00 para R$ 190,00. O juro cobrado, levando em consideração os R$ 15,00 cobrados a mais será 15: 175 = 0,085, ou seja aproximadamente 8%. É possível ainda utilizar o fator de correção, sendo 190 : 175 = 1,08, onde 1,08 corresponde ao acréscimo de 1,08 – 1  = 0,08 ou seja 8%.

O professor deve mostrar a diferença obtida ao calcular o juro da primeira e da segunda maneira, onde na primeira maneira se obteve 6% e na segunda maneira se obteve 8% e evidenciar aos alunos que os juros são calculados com base no saldo devedor.

4. Considerações finais

O professor precisa estar em constante formação, buscando sempre contribuições e estratégias metodológicas que visem aprendizagem e a formação de cidadãos ativos e críticos, pois afinal formar cidadãos é uma das funções do professor. Na disciplina de matemática é necessário levar em consideração problemas que envolvem o cotidiano dos alunos, que os levem a refletir, investigar, buscar soluções e participarem criticamente no processo do ensino e aprendizagem, isso contribuirá para que esses alunos possam tomar decisões corretas e interferir positivamente na sociedade. Atividades matemáticas sem sentido algum aos alunos faz parte do ensino tradicional, que nos dias de hoje não convém trabalhar.

A matemática financeira vai muito além de desenvolvimento de cálculos e fórmulas, trabalha-la na perspectiva da educação matemática crítica permite promover a participação dos alunos na sociedade e refletir sobre questões econômicas, tomadas de decisões e o consumo consciente. Ao apresentar a referente proposta espera-se que as aulas se tornem investigativas, provocativas, que possam integrar os alunos e que eles passem ouvintes a participantes e que os levem a refletir sobre o sistema financeiro ao qual estão inseridos.

Referências bibliográficas

BIEMBENGUT, Maria. Salett. 30 Anos de Modelagem Matemática na Educação Brasileira: Das propostas primeiras às propostas atuais. Alexandria. Revista de Educação em Ciências e Tecnologia, Florianópolis, V. 2, n. 2, p. 7-32, 2009.

Borba, M. C. Dimensões da Educação Matemática à Distância. In: Bicudo, M. A. V. & Borba, M. C. (Org.) Educação Matemática: pesquisa em movimento. São Paulo: Cortez 2004.

BRASIL. Secretaria de Educação Fundamental. Parâmetros curriculares nacionais: Matemática. Brasília : MEC / SEF, 1998. 148 p.

BRASIL. 1999b. Parâmetros Curriculares Nacionais 5ª a 8ª Série. Online, http://www.mec.gov.br, 14/10/1999.

D’AMBROSIO, U. Educação para uma sociedade em transição. Campinas, SP: Papirus 1999.

D’AMBROSIO, U. Educação Matemática: da teoria à prática. 7. ed. Campinas: Papirus, 2000.

D’AMBROSIO, U. Etnomatemática: elo entre as tradições e a modernidade. São Paulo: Autêntica, 2002.

D’AMBROSIO, U. Sociedade, cultura, matemática e seu ensino. Educ. Pesqui. v.31 n.1 São Paulo jan./mar. 2005. ISSN 1678-4634.

FREDERICO, Fernando Temporini. GIANOTO, Dulcinéia Ester Pagani. Ensino de ciências e matemática: utilização da informática e formação de professores. Zetetiké, Campinas, v. 22, n. 42, jul/dez. 2014. Disponível em: http://ojs.fe.unicamp.br/ged/zetetike/article/view/4364/5870. Acesso em: 10 de dezembro de 2016.

LENZI, Giovana da Silva. Prática de ensino em Educação Matemática: a constituição das práticas pedagógicas de futuros professores de Matemática. 2008, 106 f. Dissertação (Mestrado em Educação) - Programa de Pós-Graduação em Informática na Educação, Faculdade de Educação, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2008.

MOURA, Adelina. Mobile learning: tendências tecnológicas emergentes. In.: CARVALHO, Ana Amélia A. (Org.). Aprender na Era Digital: jogos e mobile-learning. Santo Tirso, Portugal: De Facto Editores, 2012.

PASSOS, C. M. DOS. Etnomatemática e Educação Matemática Crítica: Conexões teóricas e prática. Data da defesa: 19/06/2008. Total de folhas: 154. Dissertação de Mestrado. Belo Horizonte.

SÁ, I, P. Matemática Financeira para Educadores e Críticos, Rio de Janeiro: Editora Moderna Ltda, 2011.

SILVEIRA, E; MIOLA, R,J. Professor pesquisador em Educação Matemática. Curitiba: Ibpex, 2008.

SKOVSMOSE, O. Cenários para investigação. BOLEMA – Boletim de Educação Matemática, Rio Claro, n. 14, p. 66-91, 2000.

SKOVSMOSE, O. Educação Crítica: Incerteza, Matemática, Responsabilidade. Tradução de Maria Aparecida Viggiani Bicudo. São Paulo: Cortez Editora, 2007. 304 p.

SKOVSMOSE, O. Desafios da Educação Matemática Crítica. São Paulo: Papirus. 2008

SKOVSMOSE, O. Um convite à educação matemática crítica. São Paulo: Papirus, 2015.

SKOVSMOSE, O. Competência democrática e o conhecer na Matemática. In: _____. Educação Matemática Crítica: a questão da democracia. Campinas: Papirus Editora. 2001ª cap. 3 p. 65-96

SKOVSMOSE, O. Educação Matemática versus Educação Crítica. In: _____. Educação Matemática Crítica: a questão da democracia. Campinas: Papirus Editora. 2001ª cap. 1 p. 13-36

1. Mestranda do Programa de Pós Graduação em Ensino de Ciência e Tecnologia (UTFPR). Intérprete de Libras na Universidade Tecnológica Federal do Paraná. E-mail:mailto:solimatematica@gmail.com

2. Mestranda do Programa de Pós Graduação em Ensino de Ciência e Tecnologia (UTFPR). E-mail: mailto:julianafhbrim@gmail.com

3. Doutora em Ciência dos Materiais pela Universidade Federal do Rio Grande do Sul (UFRGS). Professora da Universidade Tecnológica Federal do Paraná. Email: sani@utfpr.edu.br

4. Doutora em Educação Cientifica e Tecnológica (UFSC). Professora da Universidade Tecnológica Federal do Paraná. E-mail: nilceiaamp@gmail.com