ISSN 0798 1015

Vol. 38 (Nº 24) Año 2017. Pág. 34

El tiempo necesario para alquilar una vivienda en Boston en 2015: Una aplicación de Regresión de Poisson Geográficamente Ponderada

The time required to rent a home in Boston in 2015: An application Geographically Weighted Poisson Regression

Jorge Enrique AGUDELO Torres 1; Diego Fernando MARTÍNEZ Montoya 2; Oscar Alonso OSPINA Espinoza 3

Recibido: 24/11/16 • Aprobado: 25/01/2017

Conteúdo

1. Introdução

2. Metodología

3. Caso de estudio

4. Resultados

5. Conclusiones

Referencias

1. Introdução

Desde las últimas décadas del siglo pasado, los trabajos relacionados con el sector inmobiliario comenzaron a utilizar modelos de precios hedónicos para tratar de explicar el precio de los inmuebles, particularmente, luego de la nueva aproximación a la teoría del consumidor propuesta por Lancaster (1966)  y de los modelos de precios hedónicos desarrollados por Rosen (1974).

En años posteriores, autores como Can (1992), Sheppard (1999), Basu y Thibodeau (1998) perfeccionaron los modelos de precios hedónicos aplicados al mercado inmobiliario reduciendo los problemas asociados a la omisión de variables relevantes. En 1998 Anselin difundió la existencia de problemas asociados a la relación espacial de los datos y a la heterogeneidad espacial.

En los inicios del nuevo milenio, Fotheringham, Brundson y Charlton (2002) desarrollaron la técnica de las regresiones geográficamente ponderadas (GWR), que facilita el desarrollo de “n” ecuaciones para “n” datos, generando múltiples ecuaciones con múltiples coeficientes, de manera que cada una de las características cuenta con un parámetro que varía de acuerdo con la ubicación en el espacio de cada dato, de manera que se minimizan los problemas relacionados con la relación espacial de los datos y con la heterogeneidad espacial.

Respecto a la utilización de modelos de Poisson con un enfoque espacial en el mercado inmobiliario, su uso ha sido restringido y se reduce a unos pocos artículos entre los que se destacan, entre otros, el realizado por Rosenthal (2011) en el que se desarrolla un modelo de precios para el mercado inmobiliario, considerando ofertas de compra que se desarrollan siguiendo un modelo de Poisson y el realizado por Cheung, Yau y Hui (2004) el que analizan el efecto de los atributos de las viviendas sobre los patrones de ventas repetidas.

En el caso de la técnica GWR, su utilización en el mercado inmobiliario ha sido poco, particularmente en Colombia, toda vez que la recolección de datos no es fácil dada la situación de seguridad del país que incentiva a los propietarios a mantener bajo reserva los valores de los inmuebles en oferta de venta o de arrendamiento.

En este trabajo se utilizan regresiones geográficamente ponderadas para buscar evidencia empírica acerca de la influencia del parque del barrio Boston, en los cánones de arrendamiento de las viviendas ubicadas en el barrio, de manera que dicha cercanía constituye una externalidad positiva para las viviendas de la zona.

Después de esta introducción, en este artículo se presenta la metodología de regresión de Poisson geográficamente ponderada, luego se explican las características del caso de estudio y de los datos utilizados y finalmente se presentan los resultados, su interpretación y algunas conclusiones relevantes.

2. Metodologia

En el caso de la Regresión Geográficamente Ponderada de Poisson, el modelo se calcula a través de un procedimiento que se conoce como mínimos cuadrados iterativamente ponderados.

Inicialmente se parte de la función de máxima verosimilitud de la distribución de Poisson para n variables:

3. Caso de estudio

3.1. Contexto

Boston es un barrio de estrato medio ubicado en la comuna La Candelaria, situada en el centro oriente de la ciudad de Medellín, Colombia, que según datos de la alcaldía de la ciudad para 2.010 contaba con 5.649 viviendas, de las cuales el 87% estaban catalogadas como estrato cuatro, el 12% como estrato tres y el restante porcentaje como estrato dos. Los datos más recientes indican que en la comuna 12, en donde se ubica el barrio, habitan 30.488 hogares, de los cuales  13.989 ocupan una vivienda en arriendo o subarriendo.

La estructura urbana del barrio es heterogénea y está conformada por viviendas bifamiliares y trifamiliares antiguas, así como por multifamiliares antiguos y algunos más recientes. De igual forma, por estar ubicado en el centro de la ciudad, el barrio cuenta con una cantidad importante de comercio en los primeros niveles de las edificaciones, aunque en su mayoría es comercio de barrio. El barrio limita al norte con el barrio Los Ángeles, al occidente con los barrios La Candelaria y Villanueva, al sur con el barrio Bomboná y al oriente con los barrios Enciso, Sucre y Caicedo.

El barrio Boston cuenta dentro de su entorno con una vía importante en la ciudad: la avenida Oriental, que permite una buena movilidad vehicular en el centro de la ciudad. Boston cuenta con una buena dotación de servicios, entre los cuales se incluyen colegios públicos, universidades,  zonas verdes, zonas deportivas, iglesias y zonas comerciales, entre otras, lo que favorece la demanda de vivienda para compra y alquiler; además, según la Lonja de Propiedad Raíz de Medellín y Antioquia, es una de las zonas en las que más rápidamente se alquila o vende una vivienda usada en la ciudad, con un promedio de tres meses.

La motivación del estudio radica en presentar un modelo de Poisson espacial para el mercado de arrendamientos de vivienda del barrio Boston, que permita predecir el tiempo que le toma a un inmueble arrendarse, dadas las características básicas del inmueble como su área o distancia al parque del barrio.

3.2. Datos utilizados

Para desarrollar el estudio se emplearon datos correspondientes a 119 cánones de arrendamiento de viviendas que se alquilaron durante el año 2015 en el barrio Boston. La muestra representa el 2.10% del total de viviendas del barrio, aunque no todas las viviendas del barrio estaban alquiladas y tampoco todas estaban en oferta de arrendamiento durante 2015.

Los datos utilizados en el trabajo fueron aportados por la Lonja de Propiedad Raíz de Medellín y Antioquia y fueron obtenidos a partir de un recorrido de campo que realiza la empresa en los principales barrios de la ciudad, dado que por la difícil situación de seguridad del país ni los propietarios ni los arrendatarios dan a conocer estas cifras. La metodología de recolección de los datos está basada en ese recorrido de campo que se hace mensualmente, detectando los anuncios de ofertas de venta y arrendamiento de vivienda. Cuando se tiene el dato, se contacta telefónicamente a la empresa o persona que ofrece el inmueble y se indaga por aspectos relacionados con el inmueble en oferta. Cada mes se verifica si el inmueble continúa en oferta o si ya ha sido comercializado. Esta metodología permite obtener datos primarios de buena calidad para realizar un seguimiento al mercado inmobiliario de la ciudad.

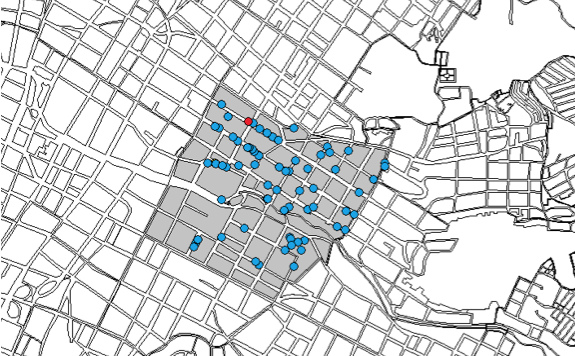
Gráfico 1. Plano de la zona

Fuente: elaboración propia con base en el software Mapinfo.

En el Gráfico 1 se observa el plano de la zona, resaltando en un color más oscuro las manzanas que hacen parte del barrio Boston. Cada punto representa un dato de un inmueble arrendado.

Las estadísticas descriptivas de la Tabla 1 muestran la diversidad de las viviendas en arrendamiento de la zona, que incluyen viviendas con cánones por metro cuadrado de entre $5.277 y $21.052, con edades entre 3 y 60 años y distancias al parque de Boston de entre 54.9 metros lineales y 458.8 metros lineales.

Tabla 1. Descripción de la muestra de viviendas.

Fuente: elaboración propia.

3.3. Definición de variables

En concordancia con los estudios de Bitter, Mulligan y Dall´erba (2007); Lu, Charlton y Fotheringham (2011); Agudelo, Agudelo, Franco, Franco (2015), las variables utilizadas en la modelación son las siguientes:

Días: Es el número de días existente entre el momento en que la vivienda sale a oferta de arrendamiento hasta el momento en que se alquila.

Canonxm2: Hace referencia al canon de arrendamiento dividido el total de metros cuadrados del inmueble. En la medida en que el canon de arrendamiento por metro cuadrado es superior, el tiempo necesario para alquilar el inmueble debe ser mayor.

Garajes: Hace referencia al número de parqueaderos privados con que cuenta la vivienda. En la medida en que tenga más garajes el tiempo necesario para alquilar el inmueble debe ser menor.

Inicio: Hace referencia al mes en el que la vivienda salió en oferta de arrendamiento al mercado, tomando a abril de 2014 como el primer mes y a noviembre de 2015 como el último. Mientras más tiempo tenga en el mercado más posibilidades tiene de alquilarse el inmueble.

Edad: Hace referencia a la edad de la vivienda. En la medida en que la edad del inmueble sea mayor, mayor será el tiempo necesario para alquilarlo.

Distancia: Esta variable hace referencia a la distancia lineal que hay entre la vivienda y el parque de Boston. Habitualmente los hogares prefieren ubicarse a cierta distancia del parque debido a que es una zona netamente comercial que genera ruido y un ambiente poco propicio para las viviendas. Se espera que a mayor distancia del parque mayor posibilidad de arrendar la vivienda.

A continuación se presentan los resultados obtenidos empleando la metodología de regresiones ponderadas geográficamente, a partir de las cuales se realizan comparaciones y se obtienen las conclusiones.

4. Resultados

Al emplear datos espaciales es necesario verificar la existencia de autocorrelación espacial, para lo cual se utiliza el estadístico conocido como I de Moran. Como se presenta en el Gráfico 2, con un valor p de 0.001, es posible afirmar con un 95% de confianza, que no existe evidencia de la existencia de no autocorrelación espacial de los datos; es decir, deben tenerse en cuenta los efectos espaciales de los datos para realizar el análisis. Para ellos se emplea una matriz de pesos espaciales W, generada con el método K-Nearest neighborhood igual a 4, ya que se asume que cada vivienda considerada tiene cuatro viviendas vecinas, en la muestra, con características similares a ella.

Gráfico 2. Valor p y función de densidad de probabilidad

Fuente: elaboración propia con base en el software GeoDa.

Una vez verificada la existencia relaciones espaciales entre las variables utilizadas, se empleó el programa GWR3 para estimar una regresión de Poisson ponderada geográficamente. Luego de nueve iteraciones, como se presenta en la Tabla 2, se obtuvo el siguiente criterio de minimización de Akaike:

Tabla 2. Ancho de Banda

A partir del modelo de regresión logística geográficamente ponderada se especificaron 119 ecuaciones, en las cuales el 97%, correspondientes a 116 casos, presentaron coeficientes de determinación superiores al 70%.

Gráfico 3. Resultados

Fuente: elaboración propia con base en el software Mapinfo.

Comparando los resultados del modelo GWPR  con un modelo OLS clásico, se observa la mayor capacidad predictiva de GWPR, como se deduce de las predicciones obtenidas en una muestra de diez datos: 

Resultados que son consistentes con la mayor capacidad predictiva y de ajuste que usualmente tienen los modelos de la familia GWR.

5. Conclusiones

En el desarrollo de este trabajo se emplearon Regresiones de Poisson ponderadas geográficamente con el fin de estudiar el impacto que tienen las características de un inmueble ubicado en Boston, en los tiempos de arrendamiento del mismo. En este sentido los modelos GWPR se presentan como los más adecuados gracias a que permiten realizar las modelaciones evitando los problemas asociados a la correlación y a la heterogeneidad espacial de los datos.

Los modelos especificados presentaron buenos niveles de ajuste en 116 de los 119 casos estudiados, mostrando que variables como el canon por metro cuadrado, la edad del inmueble y la distancia al parque de boston, entre otros, afectan el número de días en que un inmueble se encuentra en el mercado antes de ser alquilado.

Próximos trabajos estarán relacionados con la modelación de los días que le toma a un inmueble alquilarse o venderse, dadas sus características intrínsecas y extrínsecas de manera que pueda verificarse la influencia de elementos de infraestructura como aeropuertos, estadios y autopistas entre otros.

Referencias

AGUDELO, J. E.; Agudelo, G. A.; Franco, L. C.; Franco, L. E. (2015). Efecto de un estadio deportivo en los precios de arrendamiento de viviendas: una aplicación de regresión ponderada geográficamente (GWR). Ecos de Economía, 19(40), 66-80.

ALCALDÍA DE MEDELLÍN. (2010). Viviendas residenciales estratificadas por comuna y barrio, según estrato. Recuperado de: https://www.medellin.gov.co

ANAS, A. (1990). Taste heterogeneity and urban spatial structure: The logit model and monocentric theory reconciled. Journal of Urban Economics, 28(3), 31 8-335.

AUGUSTIN, N. H.; Cummins, R. P.; French, D. D. (2001). Exploring spatial vegetation dynamics using logistic regression and a multinomial logit model. Journal of Applied Ecology, 38(5), 991-1006.

AUTANT-BERNARD, C. (2006). Where do firms choose to locate their R&D? A spatial conditional logit analysis on french data. European Planning Studies, 14(9), 1187-1208.

BHAT, C. R.; Sener, I. N. (2009). A copula-based closed-form binary logit choice model for accommodating spatial correlation across observational units. Journal of Geographical Systems, 11(3), 243-272.

BASU, S.; Thibodeau, TG. (1998). Analysis of spatial autocorrelation in house prices. The Journal of Real Estate Finance and Economics, 17:61-85.

BEATY, J. (1952). Rental real estate often a good investment. Med Econ. 5(6): 93 – 94.

BITTER, C.; Mulligan, G.; Dall'erba, S. (2007). Incorporating spatial variation in housing attribute prices: a comparison of geographically weighted regression and the spatial expansion method. Journal of Geographical Systems, 9(1): 7-27.

CARL, G., & Kühn, I. (2007). Analyzing spatial autocorrelation in species distributions using gaussian and logit models. Ecological Modelling, 207(2-4), 159-170.

DEWEY, L.; DeTuro, P. (1950). Should I invest in real estate? Med Econ. 28(3): 85 – 93.

LANCASTER, K. (1966). A new approach to consumer theory. Journal of Political Economy. 74(1):132 – 157.

LEE, H. L.; Cohen, M. A. (1985). A multinomial logit model for the spatial distribution of hospital utilization. Journal of Business and Economic Statistics, 3(2), 159-168.

LI, M.; Wu, J.; Deng, X. (2013). Identifying drivers of land use change in china: A spatial multinomial logit model analysis. Land Economics, 89(4), 632-654.

LU, B.; Charlton, M.; Fotheringham, A. S. (2011) Geographically Weighted Regression Using a Non-Euclidean Distance Metric with a Study on London House Price Data. Procedia Environmental Sciences, 7, 92-97.

ROSEN, S. (1974). Hedonic prices and implicit markets: product differentiation and pure competition. Journal of Political Economy. 82: 34 – 55.

ROSENTHAL (2011) A pricing model for residential homes with Poisson arrivals and a sales deadline. Journal of real estate finance and economics. 42: 143 – 161

CHEUNG, Ute; YAU Kelvin; HUI Y, (2004) A The effects of attributes on the repeat sales pattern of residential property in Hong Kong. Journal of real estate finance and economics. 29:3 321 – 339

SELIM, H. (2009). Determinants of house prices in Turkey: Hedonic regression. Expert Systems with Applications, 36 (2), pp. 2843–2845.

SHEPPARD, S. (1999). Hedonic analysis of housing markets. En: P.C. Cheshire, E.S. Mills (Eds.), Handbook of regional and Urban Economics, vol. 3, pp. 1595–1635 North Holland, Amsterdam.

VENEGAS-MARTÍNEZ, F.; Agudelo, G.A.; Franco, L.C.; Franco, L.E. (2016). Precio del dólar estadounidense en el mundo Procesos de Itô económicamente ponderados en un análisis espacial. Economía y Sociedad. 42 (20). 83-105. México.

YU, D. (2004). Modeling housing market dynamics in the city of Milwaukee: a geographically weighted regression approach. En internet: http://www.ucgis.org/ucgisfall2004/studentpapers/files/danlinyu.pdf

ZHOU, B.; Kockelman, K. M. (2008). Neighborhood impacts on land use change: A multinomial logit model of spatial relationships. Annals of Regional Science, 42(2), 321-340.

1. Departamento de Finanzas, Instituto Tecnológico Metropolitano – ITM. Correo electrónico: agudelotorres@hotmail.com

2. Departamento de Finanzas, Instituto Tecnológico Metropolitano – ITM

3. Departamento de Finanzas, Instituto Tecnológico Metropolitano – ITM