ISSN 0798 1015

Vol. 38 (Nº 24) Año 2017. Pág. 3

O uso de inteligência artificial para a previsão do preço do petróleo

The use of artificial intelligence for forecasting oil prices

Lucas Vinicio Ribeiro IGNÁCIO 1; Luis Gustavo Alves RIBEIRO 2; Claudimar Pereira da VEIGA 3; Jackson Teixeira BITTENCOURT 4

Recibido: 28/11/16 • Aprobado: 14/12/2016

Conteúdo

1. Introdução

2 Referencial Teórico

3. Procedimentos Metodológicos

4. Aplicação e análise de resultados

5. Conclusões

Referências

1. Introdução

Para que se defina corretamente “Inteligência Artificial”, é necessário que se conheça em linhas gerais os conceitos relacionados à “inteligência”. Apesar das inúmeras controvérsias que envolvem a caracterização de inteligência, para Tveter (1998), essa tarefa torna-se mais simples de serem consideradas as capacidades esperadas de um sistema inteligente, sobre as quais há um senso comum. Tveter enumera quatro características principais inerentes e fundamentais à inteligência:

    A (i) primeira delas é o conhecimento, ou a capacidade de resolução de novos problemas. Dados previamente conhecidos serviriam de base para a avaliação de situações adversas, e o nível de eficiência com o qual essas novas situações são lidadas, ao se tentar alcançar a melhor solução possível, é um dos fatores que determinam o grau de inteligência do sistema. A (ii) segunda capacidade refere-se à velocidade de resolução de problemas. Frequentemente, em nosso dia-a-dia, atríbuí-se um conceito mais elevado de inteligência às pessoas que conseguem raciocinar e tomar decisões mais rapidamente (sem entrar no mérito do grau de assertividade de tais decisões pelo momento). Essa qualidade pode ser relacionada à otimização dos recursos disponíveis e escassos, como tempo, dinheiro e energia. A (iii) terceira característica de um sistema inteligente diz respeito à experiência. Por exemplo, para que se possa reconhecer objetos ou situações específicas, deve-se primeiramente expor o sistema à essas influências, e então, através de um processo de treinamento, o reconhecimento de padrões torna-se possível, e, por conseguinte, a identificação de uma gama de objetos e situações diversas. A (iv) quarta e última das habilidades pertinentes à inteligência e que não causa alvoroço no meio científico em virtude de sua ampla aceitação é a aprendizagem. É de se esperar que um sistema inteligente, seja ele orgânico ou não, seja capaz de aprender com os próprios erros, aprimorar seus parâmetros internos de avaliação e corrigir suas perspectivas considerando as correções necessárias.

   Com base na literatura, a Inteligência Artificial (I.A.) é o estudo das faculdades mentais pelo uso de modelos computacionais (Charniak e McDermott, 1985). Kurzweil (1990) a define, de forma mais prática, como “a arte de criar máquinas que executam funções que exigem inteligência quando executadas por pessoas”. Em outras palavras, pode-se dizer que a I.A. é a aplicação das habilidades de um sistema inteligente mencionadas por Tveter (1998) a um sistema não-orgânico. Todavia, segundo Rich e Knight (1991), as definições de I.A. existentes são muito efêmeras, pois estão profundamente atreladas ao atual estado de desenvolvimento da ciência da computação, e ainda não é considerada como uma ciência propriamente dita, estando ainda situada no campo da filosofia. De acordo com Stuart e Norvig (2004), as bases para a criação da Inteligência Artificial remontam ao século IV A.C., período no qual o filósofo Aristóteles foi o pioneiro na formulação de um conjunto preciso de leis que regem o aspecto racional da mente humana, estabelecendo um sistema básico de silogismos, que permitiriam conclusões mecânicas a partir de premissas iniciais.

    No campo da I.A., encontra-se uma ferramenta denominada como “Redes Neurais Artificiais (RNA’s). Segundo Haykin (2001), uma RNA é um mecanismo de inteligência artificial aplicado a sistemas, que tem por finalidade tentar reproduzir as habilidades de interpretação e aprendizagem do cérebro humano, com o objetivo de tornar estes sistemas mais inteligentes e dinâmicos. A utilização dessa ferramenta possui um amplo escopo de aplicação, inclusive na previsão de valores futuros a partir de séries temporais. Em oposição ao argumento de Rich e Knight (1991) de que a I.A. ainda não seria uma ciência reconhecida pelo meio acadêmico, deve-se levar em consideração o fato de seu livro ter sido publicado há mais de duas décadas. Nesse intervalo de tempo, diversos estudos, como o de Ferreira et al (2016), que auferiram a boa aderência da previsão de demanda aos dados experimentais quando utilizada uma RNA MLP para prever a demanda diária de um Centro de Tratamento de Encomendas durante 15 dias. Bundchen e Werner (2016), também comprovaram a acurácia das RNAs em previsões, estimando a demanda turística em Londres e Atenas, em que as RNAs mostraram um desempenho superior ao modelo ARIMA,   têm sido concluídos com a aplicação de sistemas inteligentes às mais variadas áreas do conhecimento, entre elas o mercado financeiro, como será demonstrado adiante.

    A motivação desta pesquisa reside no problema da volatilidade das cotações de ativos no mercado financeiro, com enfoque na cotação de fechamento do barril de petróleo brent (US$/Barril). Com isso, buscou-se criar uma ferramenta computacional baseada em Redes Neurais Artificiais, que consiga prever a cotação de fechamento do barril de petróleo brent (US$/Barril) com um nível de acerto de pelo menos 95% em relação à cotação de fechamento real.

2. Referencial Teórico

2.1 Petróleo: Breve Histórico

O Petróleo é uma commodity que deriva da decomposição de organismos que compõem o plâncton, além de restos vegetais e de animais. Esse processo de decomposição concentrou-se no fundo de lagos e mares, sofrendo as ações dos movimentos das placas tectônicas e da pressão da água durante milhões de anos, dando origem ao petróleo propriamente dito, que tende a se concentrar em rochas porosas, gerando assim as jazidas de petróleo.  Apesar de se ter conhecimento que o petróleo é utilizado desde a época dos egípcios para embalsamar os mortos e na construção de pirâmides, a extração de poços petrolíferos iniciou-se apenas em agosto de 1859. No Brasil, sua exploração foi realizada como livre iniciativa até 1938, quando Getúlio Vargas, então Presidente do Brasil, nacionalizou o solo brasileiro, criando o Conselho Nacional do Petróleo. Quinze anos mais tarde, Vargas promulgou a Lei 2004, estabelecendo monopólio estatal e criando a Petrobrás. (Unicamp, 2008)

2.2 Variabilidade nas projeções do preço do petróleo: Do pico de Hubbert ao Xisto

Em 1956, o geofísico norte-americano Marion King Hubbert previu que a produção petrolífera dos Estados Unidos atingiria seu pico em meados de 1970 (com exceção do estado do Alasca). Hoje, em comparação com a década de 1970, a produção petrolífera norte americana é 40% menor, e cerca de 70% do petróleo consumido no país é importado.

De acordo com Barros (2007):

“As conclusões de Hubbert hoje estão incorporadas a todas as projeções sobre a produção de petróleo. Como a maior parte dos grandes campos petrolíferos provavelmente já foi descoberta – a taxa de novas descobertas cai ano a ano, e as novas reservas encontradas são cada vez menores -, é possível calcular o desempenho futuro de cada país produtor, com margem de erro pequena, sendo que os diversos países do mundo estão em estágios diferentes das suas curvas de exploração.”

Apesar da tendência de queda na extração e aumento na importação de petróleo, hoje os Estados Unidos têm a maior produção doméstica de todos os tempos. Esse fenômeno, de acordo com o CME Group (Bolsa de Mercadorias de Chicago) se deve as reservas de xisto e as novas tecnologias de extração. Hoje, os Estados Unidos é o maior produtor de petróleo do mundo, com 279 milhões de barris produzidos em setembro de 2015. A Figura 1 explicita essa variabilidade, apresentando a produção norte americana de petróleo brent de Janeiro de 1920 a Setembro de 2015.

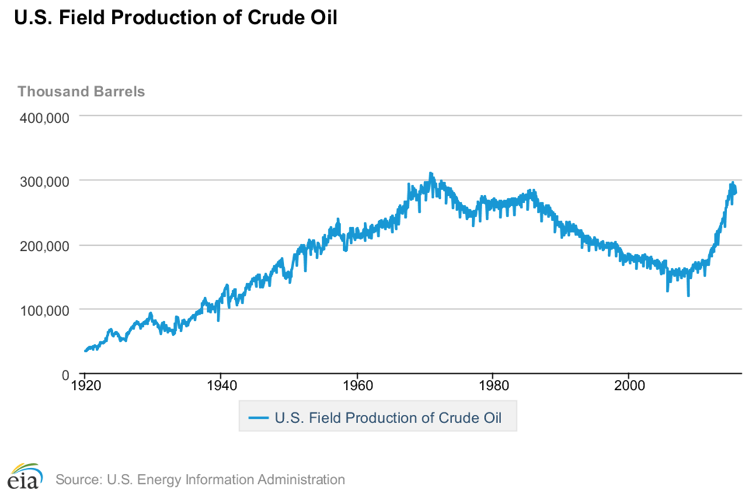
Figura 1: Produção norte-americana de petróleo brent     
Fonte: EIA/Reuters (2015)

A variabilidade na cotação apresentada na Figura 1 na produção norte americana de Petróleo é transmitida aos derivativos da commodity negociados no mercado financeiro, como ilustrado na Tabela 1 e na Figura 2, que contem as estatísticas descritivas dos retornos do Petróleo Brent originados após 1 diferenciação da matriz de preço original e o histograma destes retornos.

Tabela 1 – Retorno do petróleo brent no mercado financeiro

Tabela 1 – Retorno do petróleo brent no mercado financeiro
Fonte: EIA/Reuters (2015)

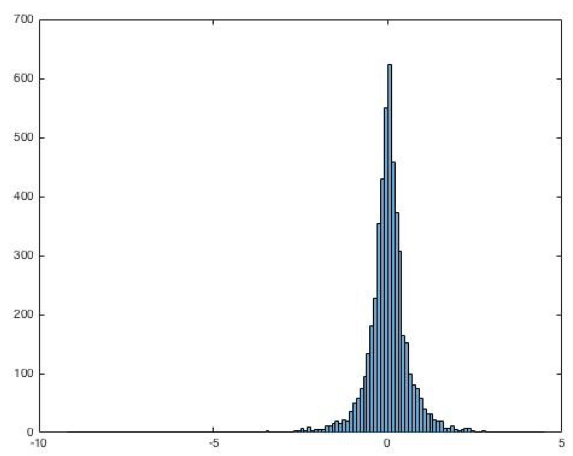
Figura 2 – Histograma dos retornos do petróleo brent no mercado financeiro
Fonte: EIA/Reuters (2015)

2.3 Importância Econômica do Petróleo

O Petróleo é a fonte de energia mais consumida no mundo, representando 42,3% do total consumido, e só deverá perder o posto de fonte principal de energia quando houver restrição em sua oferta. (BARROS, 2007) (WEIGMANN,2002). A indústria energética, como apoio para outros setores industriais, de acordo com Porter, é elemento primordial para garantir os fatores de produção do país e sua competitividade. O Governo Brasileiro, em seu site oficial, afirma que a base da economia produtiva é constituída pelo petróleo e derivativos:

“Assim, o país que detém e controla suas reservas petrolíferas e que mantém uma estrutura adequada de refino aufere vantagens competitivas, quer seja em relação à segurança interna dos setores vitais à economia, como transporte e produção de eletricidade e, por conseguinte, conferindo competitividade à indústria, quer seja em relação à sua participação no comércio internacional, por meio da exportação direta do óleo e seus derivados. Toda esta importância advém do fato de que, além de gerar combustíveis como gasolina, óleo diesel e querosene de aviação, o petróleo é também a base de uma vastagama de produtos industrializados, que vão da parafina e da nafta petroquímica aos tecidos e plásticos.”

A exportação de petróleo é um fator importante para o saldo da balança comercial brasileira. Dos 160.544.728.587 dólares exportados pelo Brasil entre janeiro e outubro de 2015, 10.233.434.653 dólares, ou 6,37% do total, são provenientes da exportação desta commodity, fazendo com que o petróleo fique apenas atrás do minério de ferro e seus concentrados em participação nas exportações brasileiras (Ministério do Desenvolvimento, 2015). A participação do setor de petróleo e gás natural, de acordo com pesquisa realizada pela Petrobrás, passou de cerca de 3% do PIB brasileiro no ano 2000 para 13% em 2014 (Petrobrás, 2000).

2.4 Petróleo no mercado financeiro

O petróleo, como instrumento financeiro, é negociado no mercado futuro de diversas bolsas de valores e mercadorias ao redor do mundo. A negociação é feita principalmente para mitigação do risco operacional via hedge. Um dos principais mercados onde se negocia o petróleo brent (Brent Oil Future) é a ICE (Intercontinental Exchange). O Brent Oil Future é negociado em contratos de um galão, cotado em dólar, com vencimento futuro.

2.5 Série temporal

A Figura 3 apresenta a série temporal utilizada para o treinamento da RNA, composta por 7.026 cotações de fechamento diário do petróleo tipo brent no mercado europeu (US$/Barril , no período de 1 de maio de 1987 a 13 de outubro de 2015.

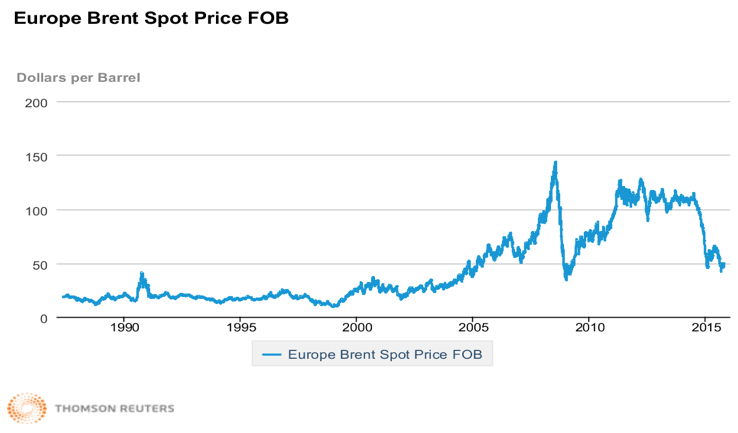
Figura 3: Série temporal do petróleo brent no mercado europeu
Fonte: EIA/Reuters (2015)

2.6 Redes Neurais Artificiais

As redes neurais artificiais (RNA’s) são modelo matemáticos que mimetizam o funcionamento de neurônios biológicos, sendo que sua capacidade computacional deriva do aprendizado e de generalizações (Braga, Carvalho & Ludemir, 2000), no entanto, este modelo tem estruturas de caixa-preta que incorporam um grande grau de incerteza sobre o seu uso em processos estáticos, dificuldade na interpretação dos resultados, problemas de treinamento e dificuldades para identificar a melhor estrutura de uma rede (Alexandridis & Zapranis, 2013; Veiga et al., 2016). A Figura 4 ilustra uma RNA genérica.

Figura 4: Rede Neural genérica
Fonte: Nunes e Pinheiro (2007).

O modelo do neurônio artificial também pode ser descrito matematicamente, conforme as equações

Nas equações 1, 2 e 3, Uk  representa a saída do combinador linear dos sinais de entrada, Xj os sinais de entrada, Wj  os pesos sinápticos, Yk o sinal de saída do neurônio, bk  o bias,φ a função de ativação e Vk  o campo local induzido (Haykin, 2001). Ainda de acordo com Haykin (2001), pode-se comparar as informações que chegam ao neurônio biológico através das sinapses às entradas de informações na rede neural artificial. Por sua vez, o corpo celular, responsável pelo processamento das informações, seria o equivalente aos pesos, somatório e ao polarizador (ou função de ativação) da RNA. Por fim, o axônio e suas terminações constituiriam a camada de saída de informações de nossa rede neural artificial. Segundo Kirsten (2009), o neurônio artificial é construído à imagem e semelhança do neurônio biológico. As similaridades incluem também a função das sinapses, que representam o processo de comunicação entre os neurônios biológicos e assume a forma de entrada de dados no neurônio artificial. Os pesos representam a relevância de cada informação inserida no sistema. Logo após multiplicar essas informações por seus respectivos pesos, a RNA efetua a soma dos valores obtidos e os polariza, limitando o valor saída das informações do sistema, de acordo com metodologia específica de cada rede neural. Segundo Prezepiorski (2003), o somatório e o polarizador (função de ativação) constituem a camada oculta do neurônio artificial, realizando a maior parte do processamento de informações do neurônio ao multiplicar os dados de entrada por seus respectivos pesos e realizar o somatório. A função de ativação também funciona como um peso para o somatório, definindo o domínio dos valores de saída do sistema (Vellasco, 2007; da Veiga, et al., 2010).

     Dentre as funções de ativação disponíveis, a sigmóide é a mais adequada ao tema proposto, pois sua estrutura melhor se identifica com o processo de aprendizado da rede, que se aprimora lentamente num primeiro momento, em seguida passa por um nível de aprimoramento interno exponencial e se estabiliza, conforme a equação 2.0:

           (4)

Na equação 1.0, x representa o valor de saída do somatório da RNA, e simboliza a Constante de Euler (aproximadamente 0,5772) e y significa o valor de saída da função de ativação sigmoide. A Figura 5 demonstra a estrutura de uma função sigmoide genérica:

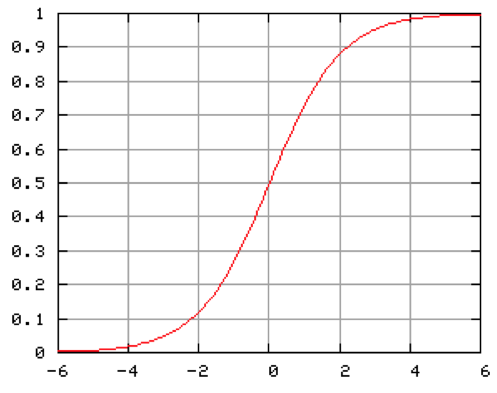
Figura 5:  Função de ativação sigmoide
Fonte: Dados de pesquisa

As RNAs são, geralmente, para dada situação específica,  excelentes Aproximadores Universal (Teorema de Aproximação Universal). De acordo com o teorema de Cybenko ou da Aproximação Universal, qualquer função contínua pode ser uniformemente aproximada por uma rede neural com pelo menos uma camada de neurônios ocultos, e com uma função de ativação sigmóide (Horie, Brizard, Guiraldelli, 2008). Rezende (2005), Haykin (2001) e Aquino (2007) enumeram diversos benefícios da utilização de redes neurais para tratamento e previsão de dados, em comparação com outras ferramentas estatísticas, tais como a análise de regressão. Dentre as principais, podemos citar três mais importantes:

A primeira é a capacidade de generalização, através das entradas de dados, as redes neurais são treinadas para reconhecer padrões, o que permite a generalização das conclusões para o processamento de informações não utilizadas no sistema. A segunda capacidade seria a flexibilidade da ferramenta, pois possui um vasto horizonte de aplicação e possibilidade de execução de grande número de tarefas simultaneamente. E, por fim, a terceira capacidade diz respeito à possibilidade de mapeamento não-linear de uma base de dados, na qual as variáveis interagem entre si de forma complexa, como é o caso de uma série temporal dos preços do petróleo em bolsas de valores. Gouvêa e Gonçalves (2013) argumentam que a principal habilidade das Redes Neurais Artificiais é o aprendizado moldado a partir das características ambientais, com o qual conseguem melhorar seu desempenho automaticamente, através da modificação dos pesos das entradas. O objetivo dessa iteração é a obtenção de um algoritmo de aprendizado que permita uma solução generalizada para certa classe de problema e que minimize o erro das saídas.

2.7 Aplicação de redes neurais artificiais no mercado financeiro

De acordo com Calôba, Calôba e Saliby (2002), as redes neurais são efetivas no tratamento de dados não-lineares, como aqueles provenientes do mercado financeiro, devido à grande complexidade de relações entre as variáveis. Até o presente momento, as RNA’s têm se mostrado com uma das melhores ferramentas para previsão de índices econômicos, como demonstram pesquisas de Almeida e Siqueira (1997) que publicaram um trabalho no qual aplicavam as redes neurais artificiais para prever níveis de falência de bancos brasileiros, sem, no entanto, obter resultados mais significativos que a aplicação do método de Regressão Logística. Adamowicz (2000) apresenta um trabalho que objetiva reconhecer padrões específicos na análise econômico-financeira de empresas que apontem características de solvência ou insolvência, também se utilizando das redes neurais. Gouvêa e Gonçalves (2013) e Harzer et al. (2016) lançaram um estudo que tenta estimar o nível de risco na concessão de crédito para novos clientes, usando as redes neurais e metodologia Multi-index em conjunto com com métodos quantitativos e qualitativos de avaliação tradicional. Da Veiga et al., (2016) analisou o uso das RNAs de Wavelets na previsão de demanda no varejo brasileiro, onde as RNAs teve desempenho superior ao modelo ARIMA (Autoregressive Integrated Moving Average).

Já Tarapanoff, Júnior e Cormier (2000) realizaram uma pesquisa de ferramentas estatísticas de gerenciamento de informações organizacionais, e chegaram à conclusão de que tais ferramentas, incluindo as redes neurais, são melhor aplicadas em organizações com fins lucrativos e estrutura administrativa bem definida, e que a aplicação de tais métodos possibilita um incremento na lucratividade dessas empresas, caso as informações disponíveis sejam corretamente tratadas. Braga, Carvalho e Ludemir (2007) verificaram a correlação de índices de diversas bolsas de valores com o Ibovespa e o impacto dessa interferência na previsão do preço de fechamento do índice, utilizando a ferramenta estatística GARCH (Generalizes Autoregressive Conditional Heteroskedasticity) e as redes neurais. Infelizmente, não houve ganho de performance com a aplicação das redes neurais na previsão do preço de fechamento do índice Ibovespa. Zou et al. (2007) comparou a performance do modelo ARIMA, redes neurais e uma combinação de modelos lineares para a previsão de preços de grãos no mercado chinês, encontrando como o melhor modelo as redes neurais. Já Filho et al (2011) compararam o desempenho de uma Rede Neural Artificial do tipo feedforward Evolutiva (RNAE) e de um modelo AR+GARCH para previsões um passo a frente de uma série temporal dos retornos do Ibovespa, e auferiram baseado no coeficiente de desigualdade U-Theil que a RNAE apresentou melhores resultados. Coelho, Santos e Costa Jr compararam previsões do tipo fora-da-amostra de modelos matemáticos de Redes Neurais Artificiais Perceptron de Multicamadas, Redes Neurais Função de Base Radial o sistema nebuloso Takagi-Sugeno e os modelos lineares ARMA-GARCH, obtendo um desempenho superior aqueles modelos matemáticos de Redes Neurais.

2.8 Tipos de redes neurais

A RNA SLP (Single Layer Perceptron), ou Rede Neural Artificial Perceptron de Camada Única, de acordo com Vellasco (2007), é uma rede neural de uma única camada oculta de neurônios, sendo apropriada para o tratamento de dados pouco complexo, cujas classes de informações sejam linearmente separáveis, conforme a figura a seguir:

A RNA MLP (Multilayer Perceptron) ou Rede Neural Artificial Perceptron de Múltiplas Camadas é uma evolução do SLP, na qual o sistema engloba duas ou mais camadas de neurônios ocultos para tratamento dos dados, e um algoritmo de retropopagação do erro, que visa minimizar o erro encontrado pela rede através de sua correção pelo treinamento supervisionado, conforme a Figura 6:

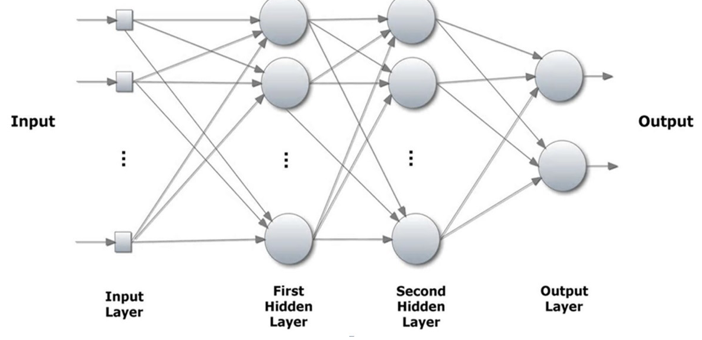
Figura 6: Rede Perceptron de Múltiplas Camadas
Fonte: Faroozesh et al, 2013.

Devido à grande quantidade de neurônios e a complexidade de suas interligações, esse modelo de rede neural é indicado para a utilização em base de dados de informações não-linearmente separáveis (Jesus e Galvanin, 2013).

Existem diversos tipo de algoritmos de retropopagação ou de treinamento possíveis de serem aplicados em uma rede neural MLP, e nesse projeto utilizaremos o algoritmo de Levenberg-Marquardt, que irá auxiliar a rede na atribuição dos pesos a cada entrada de informação no sistema, bem como na redução do MSE. De acordo com Yu e Wilamowski (2010) e Hagan e Moré (1978), o algoritmo Levenberg-Marquardt é atualmente um dos mais eficientes para treinamento de redes neurais artificiais, principalmente nos casos que envolvem extensa série temporal para treinamento da rede, sendo a elevada velocidade de convergência e de minimização de funções não-lineares a suas principais características, tendo, entretanto, as ressalvas da necessidade de múltiplas camadas ocultas de neurônios e grande capacidade computacional para que possa ser implementado.

2.9 Métricas de Desempenho do Modelo

Os erros de previsão consistem na diferença entre os valores reais e os previstos, conforme mostra a Figura 7. Os métodos de avaliação do erro utilizados neste artigo são o MSE (Mean Squared Error ou Erro quadrático médio), e o MAPE (Mean Absolute Percentual Error, ou Erro médio percentual absoluto).

Figura 7: Erros de previsão
Fonte: Morettin et al, 1981.

A escolha do MSE se fundamenta pela sua utilização por meio do ambiente computacional MatLab para definir o desempenho da rede, o momento certo de encerrar o treinamento da rede e selecionar a melhor iteração, como mostra a Figura 8:

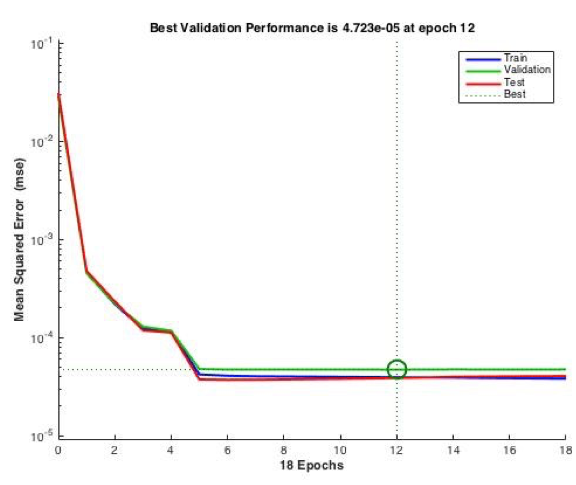
Figura 8: Melhor validação de performance pelo Matlab
Fonte: Dados de pesquisa

O MSE pode ser descrito matematicamente como apresentado na equação 5:

             (5)

Já O MAPE (Mean Absolute Percentage Error) é utilizado por seu caráter não apenas absoluto, mas sim que em consideração a média dos erros percentuais, sendo calculado a partir do preço real, explicitado na Equação 6

(6)

3. Procedimentos Metodológicos

3.1 Algoritmo de treinamento Levenberg-Marquardt

Existem diversos tipo de algoritmos de retropopagação ou de treinamento possíveis de serem aplicados em uma rede neural MLP. Nesse pesquisa, utilizou-se o algoritmo de Levenberg-Marquardt, que auxiliará a rede na atribuição dos pesos a cada entrada de informação no sistema, bem como na redução do MSE. De acordo com Yu e Wilamowski (2010) e Hagan e Moré (1978), o algoritmo Levenberg-Marquardt é atualmente um dos mais eficientes para treinamento de redes neurais artificiais, principalmente nos casos que envolvem extensa série temporal para treinamento da rede, sendo a elevada velocidade de convergência e de minimização de funções não-lineares a suas principais características, tendo, entretanto, as ressalvas da necessidade de múltiplas camadas ocultas de neurônios e grande capacidade computacional para que possa ser implementado.

4. Aplicação e análise de resultados

Para o modelos proposto, os parâmetros foram estimados pelo ambiente computacional MATLAB. Os resultados obtidos foram originados usando-se a seguinte parametrização no Neural Network Toolbox: Três neurônios na camada oculta, com cinco defasagens, a estrutura do neurônio final pode ser vista na Figura 9.

O MSE foi utilizado como medida de desempenho e o MAPE como medida de assertividade.

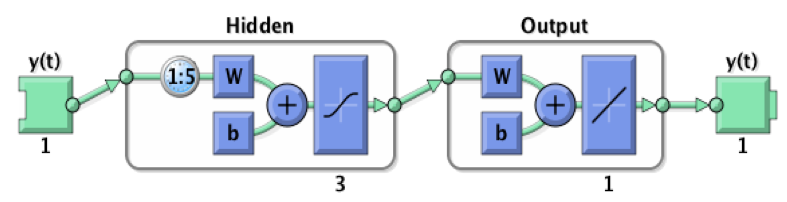
Figura 9: Estrutura da rede neural
Fonte: Dados de pesquisa

Quando executado a Rede Neural para a previsão do período de 11/09/2013 a 13/10/2015, contendo 531 observações, o desempenho (MSE) foi de 3,72491E-05. O MAPE resultante foi de 4,9612%. A Figura 10 apresenta a comparação entre valores reais e os gerados na previsão, nas cores preta e vermelha, respectivamente. O vetor x representa o número de cotações, o vetor y representa os valores das cotações e o vetor z foi inserido pelo Matlab para originar o efeito de profundidade:

Figura 10: Previsão de 11/09/2013 a 13/10/2015
Fonte: Dados de pesquisa

  Para a previsão das cotações de 02/01/2007 a 31/12/2008 (série imediatamente subsequente a utilizada para o treinamento – um passo a frente), contabilizando 503 observações, o desempenho (MSE) foi de 2,48493E-05. Já o MAPE apresentou um valor de 6,85%. A Figura 11 apresenta a comparação entre valores reais e os gerados na previsão, nas cores preta e vermelha, respectivamente. O vetor x representa o número de cotações, o vetor y representa os valores das cotações e o vetor z foi inserido pelo Matlab para originar o efeito de profundidade:

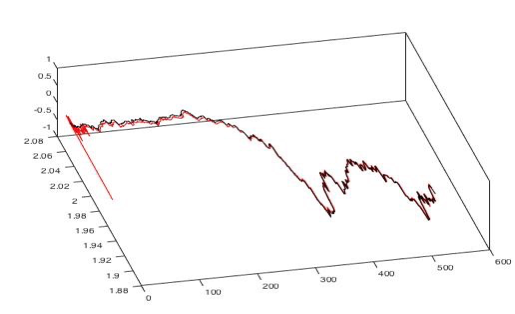
Figura 11: Previsão de 02/01/2007 a 31/12/2008
Fonte: Dados de pesquisa

Os resultados do treinamento da Rede Neural Artificial usando o algoritmo de treinamento de segunda ordem Levenberg-Marquadt são apresentados na Tabela 2. Foram utilizados 60% dos dados para treinamento, 20% para validação e 20% para teste:

Tabela 2: Resultados do treinamento da Rede Neural Artificial
Fonte: Dados de pesquisa

A assertividade da rede treinada pode ser comprovada pelos seus valores de MAPE, onde como apresentado anteriormente o período subsequente ao treinamento da rede (2007/2008) obteve MAPE de 6,85% enquanto o segundo período obteve MAPE de 4,9612%. Lewis (1997) define o nível bom de previsão quando há um MAPE menor que 10%, como afirma Veiga (2009):

Lewis (1997) descreve que, na prática, um valor de MAPE menor que 10% pode sugerir previsões potencialmente muito boas, menor que 20%, potencialmente boas e acima de 30%, potencialmente inexatas.

Considera-se, portanto, as duas previsões realizadas pela Rede Neural treinada como potencialmente muito boas.

5. Conclusões

Este artigo teve como objetivo investigar a acuracidade de uma técnica computacional, as Redes Neurais Artificiaisfeedforward, treinadas como o algoritmo Levenberg-Marquardt aplicadas às séries temporais referentes as cotações de preço do petróleo brent,  no período de de janeiro de 2007 a dezembro de 2008 e setembro de 2013 a outubro de 2015, a fim de gerar uma previsão um passo a frente. A acuracidade e aderência do modelo foi avaliada e validada  pelo menor erro MSE e MAPE.

Os resultados sugerem que para a previsão de janeiro de 2007 a dezembro de 2008 MAPE foi de 6,85% e o MSE de 2,48493e-05, e para a previsão de setembro de 2013 a outubro de 2015, o erro MAPE foi de 4,9612% e o MSE de 3,72491e-05. A principal contribuição deste artigo é demostrar que as RNAs tem uma previsão potencialmente boa para ambos os períodos analisados do Petróleo do tipo Brent. As limitações do estudo estão na janela de tempo de apenas um passo a frente, além da ausência da análise de autocorrelação e da potencial não-estacionariedade da série temporal utilizada para o treinamento.

As sugestões para trabalhos futuros baseiam se na análise e correção das violações já citadas e de testes comparativos entre os modelos não-lineares utilizados neste artigo e modelos lineares, como o ARIMA-GARCH.

Referências

Adamowicz, E. C., & Barboza, A. O. (2000). Reconhecimento de Padrões na Análise Econômico-Financeira de Empresas (Doctoral dissertation, Dissertação de mestrado. Universidade Federal do Paraná. Curitiba).

Alexandridis, A. K., & Zapranis, A. D. (2013). Wavelet neural networks: A practical guide. Neural Networks, 42, 1-27.

Almeida, F. C. de; Siqueira, J. de O. (1997). Comparação entre regressão
logística e redes neurais na previsão de falência de bancos brasileiros.
Terceiro Congresso Brasileiro de Redes Neurais, Florianópolis.

Bundchen, C., & Werner, L. (2016). Comparação da Acurácia de Previsões de Demanda Turística em Sedes Olímpicas. Revista Turismo em Análise, 27(1), 85-107.

Charniak, E. (1985). Introduction to artificial intelligence. Pearson Education India.

Ciências, D. P. D. P. G. (2003). Análise de crédito bancário com o uso de data mining: redes neurais e árvores de decisão (Doctoral dissertation, Universidade Federal do Paraná).

da Veiga, C. P., da Veiga, C. R. P., Puchalski, W., dos Santos Coelho, L., & Tortato, U. (2016). Demand forecasting based on natural computing approaches applied to the foodstuff retail segment. Journal of Retailing and Consumer Services, 31, 174-181.

da Veiga, C. R. P., Da Veiga, C. P., & Duclós, L. C. (2010). The Accuracy of Demand Forecast Models as a Critical Factor in the Financial Performance of the Food Industry. Future Studies Research Journal: Trends and Strategies, 2(2), 83-107.

de Barros, M. M. (2014). Análise da flexibilidade do refino de petróleo para lidar com choques de demanda de gasolina no Brasil (Doctoral dissertation, Universidade Federal do Rio de Janeiro).

de Pádua Braga, A. (2007). André Ponce de Leon F. de Carvalho; Teresa Bernarda Ludemir. Redes Neurais Artificiais-Teoria e Aplicações.

dos Santos Galvanin, E. A., & de Jesus, P. H. H. (2013). Redes neurais artificiais na classificação de regiões de culturas de cana-de-açúcar na região da Bacia do Alto Rio Paraguai. Revista Espacios

Ferreira, A., Ferreira, R. P., da Silva, A. M., Ferreira, A., & Sassi, R. J. (2016). Um estudo sobre previsão de demanda de encomendas utilizando uma rede neural artificial. Blucher Marine Engineering Proceedings, 2(1), 353-364.

Foroozesh, J., Khosravani, A., Mohsenzadeh, A., & Mesbahi, A. H. (2013). Application of Artificial Intelligence (AI) modeling in kinetics of methane hydrate growth. American Journal of Analytical Chemistry.

Gonçalves, E. B. (2005). Análise de risco de crédito com o uso de modelos de regressão logística, redes neurais e algoritmos genéticos (Doctoral dissertation, Universidade de São Paulo).

Harzer, J. H., Souza, A., Silva, W. V., Cruz, J. A. W., & Veiga, C. P. (2016). Probabilistic approach to the MARR/IRR indicator to assess financial risk in investment projects. International Research Journal of Finance and Economics, 144, 131-146.

Haykin, S. S. (2001). Redes neurais. Bookman.

Kirsten, H. A. (2009). Comparação entre os modelos holt-winters e redes neurais para previsão de séries temporais financeiras (Doctoral dissertation, Pontifícia Universidade Católica do Paraná).

Kurzweil, R., Richter, R., & Schneider, M. L. (1990). The age of intelligent machines (Vol. 579). Cambridge: MIT press.

Lakatos, E. M., & Marconi, M. D. A. (2010). Fundamentos da metodologia científica. In Fundamentos da metodologia científica. Altas.

Nunes, G. B.; Pinheiro, R. B.. O que são Redes Neurais Aritificiais?. Disponível em: <http://webserver2.tecgraf.puc-rio.br/~mgattass/RedeNeural/redeneural.html>. Acesso em: 13 abril 2015.

Porter, M. E. (1986). Estratégia competitiva: técnicas para análise de indústrias e da concorrência. Campus.

Rezende, S. O. (2003). Sistemas inteligentes: fundamentos e aplicações. Editora Manole Ltda.

Rich, E., & Knight, K. (1991). Artificial intelligence. McGraw-Hill, New.

Stuart, R., & Norvig, P. (2004). Inteligência artificial. Tradução de PubliCare Consultoria–Rio de Janeiro, RJ: Elsevier, 28-29.

Tarapanoff, K., Araújo Júnior, R. H. D., & Cormier, P. M. J. (2000). Sociedade da informação e inteligência em unidades de informação. Ciência da Informação, Brasília, 29(3), 91-100.

Tveter, D. (1997). The Pattern Recognition Basis of Artificial Intelligence. IEEE Press.

U.S. Energy Information and Administration (EIA). Disponível em: <http://www.eia.gov>. Acesso em: 20 set 2015.

Vellasco. M. B. R. Redes Neurais Artificiais. Disponível em: <http://www2.ica.ele.puc-rio.br/Downloads%5C33/ICA-introdu%C3%A7%C3%A3o%20RNs.pdf>. Acesso em: 26 abril 2015.

Wilamowski, B. M., & Yu, H. (2010). Improved computation for Levenberg–Marquardt training. IEEE Transactions on Neural Networks, 21(6), 930-937.

Zou, H. F., Xia, G. P., Yang, F. T., & Wang, H. Y. (2007). An investigation and comparison of artificial neural network and time series models for Chinese food grain price forecasting. Neurocomputing, 70(16), 2913-2923.

1. Pontifícia Universidade Católica do Paraná – PUCPR. Email: Ribeiro.lucas@vernati.com.br

2. Pontifícia Universidade Católica do Paraná - PUCPR. Email: Luis_garibe@gmail.com.br

3. Pontifícia Universidade Católica do Paraná - PUCPR . Email: Claudimar.veiga@pucpr.br

4. Pontifícia Universidade Católica do Paraná - PUCPR. Email: Jackson.bittencourt@grupomarista.org.br