ISSN 0798 1015

Vol. 38 (Nº 02) Año 2017. Pág. 2

El problema de carga de pallets en centros de distribución utilizando diseño de mezclas

Pallet loading problem in distribution centers using mixture experiments

Fernando SALAZAR Arrieta 1; Rodrigo Andrés GOMEZ Montoya 2; Jose Alejandro CANO 3

Recibido: 28/07/16 • Aprobado: 18/08/2016

Contenido

1. Introdución

2. Generalidades de los CEDI y el estibado

3. Metodología

4. Resultados y discusión

5. Conclusiones

Referencias

1. Introducción

El estibado es una operación logística que permite acomodar productos, generalmente cajas, sobre una estiba para conformar una unidad de carga que facilita el almacenamiento, manipulación, despacho y transporte de los productos en el sistema logístico de las empresas. Por estos motivos, un adecuado método de estibado no sólo genera impacto en la eficiencia de las operaciones respecto a costos y tiempos en los procesos logísticos, sino también mejora la satisfacción de los requerimientos de los clientes.

Por los motivos expuestos, el presente artículo tiene como objetivo utilizar el diseño de mezclas como método cuantitativo para mejorar el estibado de productos en Centros de Distribución (CEDI), de tal forma que permita reducir el tiempo de la operación. De esta manera, se busca contribuir al desarrollo de la investigación en tópicos relacionados con el aumento del desempeño de un CEDI. Para alcanzar el objetivo propuesto, se utiliza una metodología que adapta un diseño de mezclas para el estibado (identificación de factores, variables de respuesta, modelo estadístico y análisis con el software estadístico Minitab 15®). Adicionalmente, se emplea un estudio de caso aplicado en el CEDI de una cadena de supermercados en la ciudad de Medellín. Debe indicarse, que se emplea información primaria (datos del CEDI y el estibado) y secundaria (libros y artículos científicos) para desarrollar el documento.

El artículo se estructura en cuatro partes. En la primera parte, se realiza una revisión del marco teórico y el estado del arte del estibado en los CEDI. En la segunda parte, se presenta la metodología del diseño de mezclas utilizado en el proceso de estibado. En la tercera, parte se desarrolla la metodología junto a un caso de aplicación en el CEDI de un supermercado. En la cuarta parte, se presentan las conclusiones obtenidas del artículo.

2. Generalidades de los CEDI y el estibado

En la última década la logística empresarial ha cobrado importancia, ya que esta permite planear, ejecutar y controlar los flujos de información, productos y dinero desde el proveedor de materias primas, insumos y servicios pasando por la transformación para obtener productos terminados, los cuales, son almacenados y transportados para satisfacer las necesidades de los clientes buscando operar a costos mínimos (Manners-Bell, Cullen, y Roberson, 2014; Waters & Rinsler, 2010).

Dentro del contexto de la logística, los CEDI son un tipo de almacén que permiten regular la oferta y la demanda entre la empresa y los clientes a través de una adecuada administración de los inventarios y la gestión de operaciones tales como: recepción, acomodo, almacenamiento, preparación de pedidos, despacho y crossdocking (Baker, 2008). Por su parte, Baker y Halim (2007) describen que un CEDI a menudo es considerado como un punto en la cadena de suministro que permite consolidar productos, agregar servicios de valor y despachar pedidos a los consumidores de una manera eficiente.

Para las empresas dentro de la cadena de suministro, la adecuada gestión del CEDI no sólo contribuye a satisfacer las necesidades de los clientes en las condiciones pactadas de cantidad, calidad y tiempo de entrega, sino a operar a costos adecuados, ya que este proceso representa aproximadamente el 20% de los costos y gastos logísticos de la empresa (Baker y Halim, 2007). De allí la importancia de su planeación, ejecución y control.

En los CEDI se almacenan, consolidan o desconsolidan productos provenientes de diferentes proveedores o fabricas para atender los requerimientos de los clientes en la cadena de suministro (Frazelle, 2001). Generalmente en los CEDI, se utilizan unidades de carga denominadas Pallets o estibas, los cuales permiten consolidar los productos en una sola carga con el fin de facilitar el almacenamiento, manipulación, despacho y transporte de los productos en el sistema logístico (He, Wu, y de Souza, 2012). Esta situación, conlleva a la necesidad de diseñar e implementar métodos de estibado dentro del CEDI para acomodar adecuadamente los productos en las estibas, además de desarrollar este proceso en el tiempo y condiciones adecuadas, contribuyendo debidamente a la eficiencia y la eficacia empresarial.

2.1 Estibado en los CEDI

En el ámbito de la manufactura, la logística y los CEDI, el estibado es un proceso que impacta en la eficiencia de las operaciones y prestación del servicio al cliente. Para He et al. (2012), este problema es importante, ya que a pesar de diferentes investigaciones científicas que desarrollan métodos de estibado, en las  empresas este proceso logístico es realizado con base a la experiencia y juicio de los trabajadores, lo cual, puede afectar su eficiencia y eficacia.

El estibado es un proceso que consiste en organizar cajas o productos en una estiba o pallet rectangular, buscando maximizar la cantidad de cajas o productos acomodados en el área y volumen disponible (Letchford y Amaral, 2001). Para Pureza y Morabito (2006), cuando se tiene gran cantidad de cajas para estibar, estas deben ser acomodadas ortogonalmente, con sus lados posicionados paralelos a la base de la estiba, buscando de esta manera mejorar el uso del área disponible.

El problema de estibado o es clasificado como un problema de dos dimensiones considerando las variables de largo y ancho de las cajas, las cuales, se convierten en restricciones importantes para maximizar el número de cajas que pueden acomodarse en la estiba. De acuerdo con Kocjan y Holmström (2010), en el proceso de estibado deben considerarse algunas condiciones, tales como: no traslapar la cajas; asegurar la estabilidad de la carga; proteger los productos estibados utilizando en la medida de lo posible una envoltura de plástico o materiales similares de embalaje; seleccionar un modelo de distribución de las cajas en la estiba que permita un adecuado uso del área, el volumen y la estabilidad de la carga.

En los CEDI el estibado de productos generalmente es necesario para el proceso de almacenamiento, despacho y transporte, ya que permite consolidar los productos en estibas, lo cual mejora el uso del espacio en el almacén y facilita la manipulación de los productos, impactando en el aumento de la eficiencia, reducción de costos y agilización de las operaciones en el CEDI, que a su vez permite aumentar potencialmente el nivel de servicio a los clientes (Letchford y Amaral, 2001; Pureza y Morabito, 2006).

Para el diseño de los métodos de estibado se identifica en la literatura el uso de diferentes técnicas cualitativas métodos cuantitativos. Las técnicas cualitativas involucran la experiencia y juicio de los operarios encargados del estibado. Entre los métodos cuantitativos, se considera el uso de algoritmos exactos, heurísticos, metaheurísticos y métodos estadísticos que buscan obtener soluciones óptimas o cercanas a esta, con el fin de maximizar la cantidad de cajas o productos ubicados en la estiba, o minimizar el tiempo de esta operación (Dereli y Sena, 2010; He et al., 2012; Kocjan y Holmström, 2010). Los algoritmos exactos suelen ser utilizados para resolver problemas de estibado pequeños debido a lo robusto de los modelos matemáticos, lo cual, limita la optimización debido a la capacidad computacional (He et al., 2012). Respecto, a los heurísticos y metaheurísticos, estos generan soluciones cercanas a la óptima, con mayor velocidad computacional respecto a los algoritmos exactos que utilizan generalmente modelos de programación lineal (Dereli y Sena, 2010; He et al., 2012). En el estibado pueden utilizarse modelos de diseño de experimental, tales como el modelo de mezclas, el cual identifica y establece qué niveles de los factores deben emplearse en el estibado de las cajas en la estiba, buscando reducir el tiempo de la operación.

A continuación, se presentan algunos artículos identificados y revisados en la literatura científica relacionada con el estibado de cajas en la logística y en los CEDI.

Tabla 1. Revisión en la literatura científica del problema de estibado

Fuente: Elaboración propia

A partir de la revisión del estado del arte, se identifica que en el problema de estibado se utilizan diferentes enfoques basados en el uso de herramientas cuantitativas, tales como los algoritmos exactos con programación lineal y no lineal entera, heurísticos y metaheurísticos. Dentro de los metaheurísticos se encuentran la búsqueda tabú y los algoritmos genéticos, los cuales, permiten obtener soluciones pseudóptimas que se acomodan en la estiba. Además, estos metaheurísticos incluyen criterios de estabilidad de la carga y rentabilidad en la operación.

Igualmente, para el problema de estibado puede utilizarse el diseño de experimentos de mezclas, ya que este tiene como objetivo identificar cuáles productos deben estibarse con el propósito de aumentar el desempeño, que en el contexto de este proceso logístico puede relacionarse con el aprovechamiento del espacio o la reducción del tiempo. Lo anterior impacta en la eficiencia y la satisfacción de las necesidades de los clientes (Gutiérrez y De la Vara, 2012).

Una ventaja que ofrece el uso de diseño de mezclas en el problema de estibado es que considera las proporciones de los productos a estibar, en vez de las cantidades absolutas de productos. Lo anterior, permite identificar y configurar los factores del proceso de estibado para que se alcancen valores de la variable respuesta planeados para atender los requerimientos de los clientes, u otros procesos logísticos tales como el almacenamiento (Gutiérrez y De la Vara, 2012). Otro aspecto, que debe resaltarse del diseño de mezcla es que los análisis y resultados tienen validez estadística, y permite realizar experimentos planeados en el diseño o mejoramiento del proceso de estibado en el CEDI.

Por lo tanto, el uso de diseño de mezclas en el problema de estibado de carga permite explorar y desarrollar soluciones que aporten al mejoramiento de variables de respuesta, entre las cuales se encuentran el tiempo de proceso, uso de espacio y estabilidad de carga.

3. Metodología

Para alcanzar el objetivo propuesto se utiliza una metodología de diseño de mezclas para el estibado de cajas en el CEDI. Esta metodología cubre desde la descripción del CEDI y proceso de estibado, planeación del diseño de mezclas, realización de los experimentos para la configuración de los pallets, análisis estadístico y resultado de configuración de estibado (Gutiérrez y De la Vara, 2012). Para realizar el análisis estadístico se utiliza el software Minitab 15®. En la Figura 1 se representa la estructura de la metodología, y cada uno de los componentes.

Figura 1. Metodología para el estibado de carga con diseño de mezclas

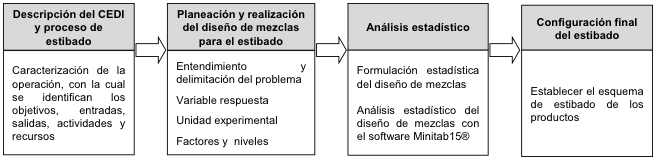
Fuente: Elaboración propia

Con la metodología descrita, se busca adaptar el uso del modelo de diseño experimental de mezclas para el estibado de carga en un CEDI que atiende los requerimientos de un grupo de supermercados ubicados en la ciudad de Medellín. De otra parte, la metodología tiene una estructura planeada y controlada, ya que en la planeación, se establece la variable respuesta, los factores y la unidad experimental relacionada con el estibado realizando de esta manera una experimentación eficiente que contribuya al adecuado desempeño del CEDI, con lo cual se deben los costos, el tiempo y la satisfacción de las necesidades de los clientes. Por su parte, el análisis estadístico permite identificar y evaluar qué niveles de los factores deben seleccionarse para que se alcance el desempeño planeado o requerido en el estibado.

4. Resultados y discusión

A continuación se presentan los resultados obtenidos para cada uno de los componentes de la metodología propuesta.

4.1 Descripción del CEDI y el Estibado

El CEDI elegido tiene como objetivo recibir los productos comprados a los proveedores y atender los requerimientos de los supermercados, garantizando condiciones de calidad, cantidad, referencias y tiempos de entrega. Adicionalmente, en el CEDI se reciben, almacenan, preparan y despachan diferentes tipos de referencias de productos, entre las cuales se encuentran alimentos, enlatados, jabones y detergentes, frutas y verduras, entre otros. Es importante establecer que según la naturaleza de los productos se utilizan diferentes unidades de carga tales como estibas o pallets, cajas, pacas o unidades individuales de empaque.

Respecto a la infraestructura y los recursos, el CEDI cuenta con un área de 3000 m2 y dos muelles de recepción y despacho. Los recursos que se utilizan son el recurso humano, conformado por seis operarios y un coordinador de proceso; equipos de manejo de materiales conformados por dos transpaletas y una montacarga; y Tecnologías de Información y Comunicación (TIC)representadas por un módulo transaccional del ERP de la compañía que permite el registro de ingresos, salidas y administración de inventarios.

El estibado en el CEDI se realiza en la operación de despacho, dónde los operarios configuran la estiba según el pedido que debe enviarse a cada supermercado. Se resalta que los operarios utilizan el método de estibado basado en la experiencia y juicio de estos. En la Tabla 2 se presenta una caracterización de la operación de despacho y estibado de la carga a través del método SIPOC (Supplier o proveedor, Input o entrada, Process o proceso, Output o salida, Costumer o consumidor).

Tabla 2. Caracterización de la operación de despacho y estibado en el CEDI

Fuente: Elaboración propia

4.2 Planeación y realización del experimento

A partir de la descripción del CEDI, el estibado y el despacho, se obtiene la información para comenzar con el uso del modelo de mezclas para el estibado de los productos.

4.2.1 Entender y delimitar el problema

En la actualidad, en el CEDI de la cadena de supermercados en la ciudad de Medellín se ha identificado que el estibado de los productos despachados es ineficiente en el uso del espacio de la estiba y en el tiempo que los operarios consumen en el estibado, lo cual, afecta el tiempo de entrega a los clientes, causando retrasos en el despacho que se encuentra entre 5 y 7 minutos aproximadamente. El tiempo de estibado en promedio es de 29 a 30 minutos para un pedido estándar de 97 cajas. Por estos motivos, se identifica como una oportunidad utilizar el diseño de mezclas para establecer un método de estibado que permita reducir el tiempo de esta operación, y de esta manera contribuir al mejoramiento en el CEDI.

El estibado o configuración de las estibas consiste en seleccionar la mezcla de productos que se pueden agrupar para despacharlos y enviarlos a los diferentes supermercados que conforman su circuito logístico, con el fin de atender sus necesidades. En el CEDI se tienen q productos que se requieren mezclar para el estibado en el CEDI de la cadena de supermercados. Específicamente la aplicación de mezclas se centrará en tres familias de alimentos procesados (pastas, caldo de gallina, y salsas de tomate), las cuales vienen empacadas en cajas con diferentes tamaños. Adicionalmente, se debe considerar que cada producto tiene diferente grado de fragilidad que limita su manipulación.

4.2.2 Variable respuesta

Tiempo promedio de configuración de la estiba, considerando que el peso promedio de la carga (cada caja) es de 35 kg.

4.2.3 Unidad experimental

Estibas con un peso de carga promedio de 1250 kg, configuradas con las familias de productos, que equivalen aproximadamente a 12 cajas en cada una de estas (3 familias).

4.2.4 Factor de interés y niveles

Las proporciones de cajas de familias de productos para el estibado se denominan como x₁ (proporción de cajas con 20 paquetes de pastas), x₂ (proporción de cajas con 3000 cubos de gallina) y x₃ (cajas con 24 frascos de salsa de tomate de 400 gramos). Estos factores y niveles se seleccionan al ser las referencias de productos que más suelen incluirse en los pedidos de los clientes, y su inadecuado estibado y despacho afecta potencialmente el desempeño del CEDI.

4.3 Análisis estadístico

Este apartado presenta la estructura de los datos del diseño de mezclas de productos para seleccionar la configuración de la estiba, incluyendo el ajuste de su modelo estadístico, caracterización de la superficie de respuesta y restricciones de los componentes de una mezcla. Finalmente, se interpretan los resultados del análisis para tener la información necesaria que permita a los ingenieros del CEDI tomar la decisión para lograr una operación de despacho adecuada.

4.3.1 Estructura de datos para el diseño de mezclas

Para la captura de datos del diseño se procede a probar diferentes porcentajes de cada familia de productos en la estiba y medir el tiempo promedio para su estibado. La Tabla 3 presenta los resultados de un estudio previo que ha establecido las familias de productos que pueden estibarse juntas, con el fin de no afectar la calidad del producto.

Tabla 3. Estructura de datos del diseño de mezclas de cajas

Fuente: Elaboración propia

Con las combinaciones de proporciones de referencias de productos, se evalúa y experimenta el comportamiento del tiempo promedio de estibado para el caso en el cual se estiba un solo producto i o si por lo contrario, se combinan varias referencias de producto en una estiba. De esta forma, para cada producto i se debe satisfacer que 0 ≤ x₁ ≤ 1, y que x₁ + x₂ + x₃ = 1 para garantizar que las proporciones de los productos varíen entre 0 y 1 y que los productos se manejen dependientemente entre sí.

Para determinar el estibado más adecuado para configurar la estiba, se utiliza un diseño de mezclas simplex-reticular {3,2} de tres componentes de productos en caja (q=3) y de orden m=2, con lo cual se generan tres puntos del diseño para cada referencia de producto i que se forman con . Con estos puntos, se pueden formar las siguientes mezclas de referencias para realizar el estibado . Además de esto, se aumenta el diseño con corridas internas, las cuales corresponden al centroide global  y las mezclas de cajas ubicadas entre el centroide y los vértices .

4.3.2 Análisis estadístico con el software Minitab15®.

La Figura 2 representa gráficamente este diseño de mezclas reticular (q=3) y orden m=2, aumentado con pseudocomponentes para evitar problemas de multicolinealidad, que son usuales en este tipo de diseños.

Figura 2. Diseño simplex reticular configuración de estibas

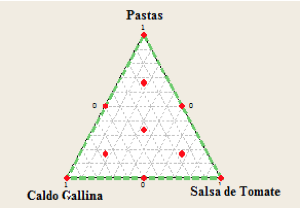
Fuente: Elaboración propia

Para determinar si el diseño de mezclas de configuración de estibas se ajusta a un modelo lineal, cuadrático o cúbico especial, se realiza un análisis ANOVA que evalúa los modelos con el criterio del valor p, identificando cuál de estos es significativo o aporta elementos en la explicación de la respuesta. De la Tabla 4, se identifican los modelos que presentan un valor p bajo, por lo cual se ajustan al diseño de mezclas. Por su parte, Gutiérrez y De la Vara (2012) indican que en estos casos, se selecciona el modelo de mayor complejidad u orden.

Tabela 4. Análisis de los posibles modelos para la configuración de estibas

Fuente: Elaboración propia

De esta forma se selecciona el modelo cuadrático que tiene un valor p de 0.021, con R2 ajustado de 88.66%. La Tabla 5 presenta la estimación de los coeficientes del modelo cuadrático.

Tabla 5. Estimación de coeficientes de regresión de modelo cuadrático

Fuente: Elaboración propia

Se identifica así que los coeficientes del modelo son significativos respecto a la variable de respuesta, es decir, respecto al tiempo de estibado. A continuación, la ecuación (1) presenta el modelo cuadrático de regresión para el problema logística en análisis.

El modelo de regresión cuadrático de la ecuación (1) representa la forma para estimar el tiempo promedio de configuración de la estiba. Se debe indicar que el coeficiente de las cajas con cubos de caldo de gallina predomina, seguido de las cajas de pastas y frascos de salsa de tomate. En cuanto a la interacción entre las cajas de pastas con cajas de cubos de caldo de gallina y la interacción entre cajas de pastas con cajas de salsa de tomate son sinérgicas, la interacción entre cajas de cubos de caldo de gallina y cajas salsa de tomate son antagónicas.

En la Figura 3 y Figura 4 se presenta respectivamente la superficie de respuesta y las superficie de contorno para identificar las mezclas que permiten reducir el tiempo de configuración de estibas de los tres tipos de productos. Con estos resultados es posible tomar las decisiones de las combinaciones de cajas de los tres productos en el CEDI.

Figura 3. Superficie de mezcla de tiempo de estibado

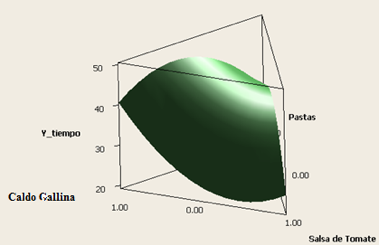
Fuente: Elaboración propia

Figura 4. Superficie de contorno de la mezcla de tiempo de estibado

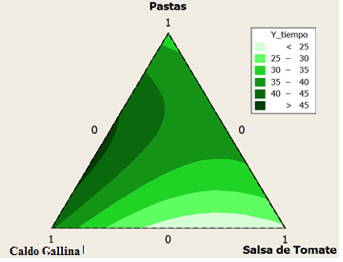
Fuente: Elaboración propia

4.4 Resultados de la configuración del estibado

A partir de la aplicación del diseño de mezclas de las cajas de pastas, cubos de caldo de gallina y frascos de salsa de tomate, con base en el modelo ajustado cuadrático que permite encontrar el valor esperado del tiempo promedio de configuración de estiba, y de acuerdo con las gráficas de superficies de respuesta y contorno, se obtienen los siguientes análisis:

La combinación de 50% cajas con cubos de gallina y 50% con cajas de salsa de tomate en la estiba, sin incluir cajas con pastas, permite alcanzar un tiempo promedio de configuración de estiba menor a 25 minutos.  En términos de diseño de experimentos un punto de mezcla . Una configuración de estibas que permite alcanzar tiempos promedios de esta operación de 25 a 30 minutos, es la combinación de 16.66 % de cajas de pastas y cubos de gallina respectivamente, y un 66.67% de cajas con frascos de salsas de tomate. Este punto de mezcla es .

Finalmente, se puede indicar que el modelo de mezclas ofrece otras opciones que pueden ser elegidas según las condiciones técnicas y económicas de la empresa de cadena de supermercados en su centro de distribución.

5. Conclusiones

El estibado es una operación utilizada en los procesos logísticos, permitiendo ubicar productos en una estiba con el fin de conformar una unidad de carga que facilita el almacenamiento, manipulación, despacho y transporte de los productos. De allí, la importancia de su adecuada configuración para contribuir a la eficiencia y eficiencia en el sistema logístico.

Se identificaron diferentes técnicas cualitativas y cuantitativas que pueden ser utilizadas en el estibado de la carga en los CEDI. Entre las cualitativas, se encuentra la experiencia o juicio de los operarios. Por su parte, las cuantitativas, se consideran los algoritmos exactos que emplean programación lineal, heurísticos y metaheurísticos (búsqueda tabú, algoritmos genéticos, entre otros).

Adicionalmente, se identifica la oportunidad de utilizar un modelo de diseño de mezclas, el cual, permite establecer diferentes proporciones o combinaciones de producto, con el fin de aumentar el desempeño respecto al mejor aprovechamiento del espacio o reducción del tiempo de operación. Con el uso del diseño de mezclas para el estibado, se adapta un modelo estadístico que permite desarrollar propuestas en el estado del arte del tema, y establecer métodos de estibado que con validez estadística permitan mejorar esta operación en los CEDI.

La aplicación del diseño de mezclas simplex-reticular {3,2}, con tres componentes denominados cajas de pastas, caldo de gallina y salsa de tomate (q=3) y orden m=2, el cual se basa en el modelo ajustado cuadrático, permite encontrar el valor esperado del tiempo de configuración de estiba. En este sentido, las gráficas de superficies de respuesta y contorno establecen que la combinación de 50% cajas con cubos de gallina y 50% con cajas de salsa de tomate 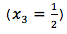en la estiba, sin incluir cajas con pastas, permite alcanzar un tiempo promedio de configuración de estibas menor de 25 minutos para atender el pedido de los clientes, lo cual representa una reducción de 4 minutos o 14% respecto al tiempo actual de la operación. De esta manera, puede mejorarse la operación, y contribuir a la agilización del despacho y el transporte.

Finalmente, como trabajo futuro se identifica el uso conjunto del diseño de mezclas con metaheurísticos o simulación discreta, con el fin de mejorar las capacidades de estibado, ya que el modelo de mezclas permite realizar experimentos planeados y controlados para aumentar el desempeño, y los metaheurísticos permiten simular el comportamiento del tiempo o aprovechamiento del espacio de la estiba.

6. Referencias

Baker, P. (2008). The design and operation of distribution centres within agile supply chains. International Journal of Production Economics, 111(1), 27–41.

Baker, P., y Halim, Z. (2007). An exploration of warehouse automation implementations: cost, service and flexibility issues. Supply Chain Management: An International Journal, 12(2), 129–138.

Che, C. H., Huang, W., Lim, A., y Zhu, W. (2011). The multiple container loading cost minimization problem. European Journal of Operational Research, 214(3), 501–511.

Dereli, T., y Sena, G. (2010). A hybrid simulated annealing algorithm for solving multi-objective container-loading problems. Applied Artificial Intelligence: An International Journal, 24(5), 463–486.

Frazelle, E. H. (2001). World-Class Warehousing and Material Handling. United States: McGraw Hill Professional.

Gutiérrez, H., y De la Vara, R. (2012). Análisis y diseño de experimentos. 3a Edición. México, D.F.: McGraw-Hill.

He, Y., Wu, Y., y de Souza, R. (2012). A global search framework for practical three-dimensional packing with variable carton orientations. Computers & Operations Research, 39(10), 2395–2414.

Kocjan, W., y Holmström, K. (2010). Computing stable loads for pallets. European Journal of Operational Research, 207(2), 980–985.

Lau, H. C. W., Chan, T. M., Tsui, W. T., Ho, G. T. S., y Choy, K. L. (2009). An AI approach for optimizing multi-pallet loading operations. Expert Systems with Applications, 36(3), 4296–4312.

Letchford, A. N., y Amaral, A. (2001). Analysis of upper bounds for the Pallet Loading Problem. European Journal of Operational Research, 132(3), 582–593.

Manners-Bell, J., Cullen, T., y Roberson, C. (2014). Logistics and Supply Chains in Emerging Markets. London: Kogan Page Publishers.

Martins, G. H. A., y Dell, R. F. (2008). Solving the pallet loading problem. European Journal of Operational Research, 184(2), 429–440.

Pureza, V., y Morabito, R. (2006). Some experiments with a simple tabu search algorithm for the manufacturer’s pallet loading problem. Computers & Operations Research, 33(3), 804–819.

Waters, D., y Rinsler, S. (2010). Global Logistics: New directions in supply chain management. London: Kogan Page Publishers.

1. Facultad de Ciencias Económicas, Pontificia Universidad Javeriana, Colombia. Ingeniero Mecánico, Magister en Planeación Estratégica y Dirección de Tecnología, Doctor en Logística y Dirección de la Cadena de Suministro. fsalazar.network.com@gmail.com

2. Grupo de investigación GILACS, ESACS - Escuela Superior en Administración de Cadena de Suministro. Ingeniero Industrial, Magister en Ingeniería Administrativa, Doctor en Ingeniería. rodrigomezm1986@gmail.com

3. Grupo de investigación GILACS, ESACS - Escuela Superior en Administración de Cadena de Suministro. Ingeniero Industrial, Magister en Ingeniería Administrativa. joseale84@hotmail.com