HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 35) Año 2016. Pág. 22

Otimização da exportação da soja brasileira: uma aplicação de um modelo de design de rede

Optimization of Brazilian soybean exports: an application of a network design model

Ana Paula MILANEZ 1; Andréa Leda Ramos de OLIVEIRA 2; Anibal Tavares de AZEVEDO 3; Takaaki OHISHI 4

Recibido: 28/06/16 • Aprobado: 28/07/2016

Conteúdo

1. Introdução

2 Descrição do Problema

3 Resultados e Discussão

4 Conclusão

Referências Bibliográficas

1. Introdução

O desenvolvimento dos negócios agrícolas vem ocorrendo de forma pujante na economia brasileira, caracterizando-se por cadeias produtivas cada vez mais integradas e pelo uso intensivo de capital nos diversos segmentos que o compõe. Para corroborar tal fato, vale destacar alguns aspectos, tais como: a elevada participação no PIB, manutenção do saldo positivo da balança comercial e a contribuição para o controle da inflação, evidencia-se sua importância para o desempenho da economia brasileira (OLIVEIRA; SILVEIRA, 2013).

A cadeia produtiva da soja é um dos segmentos que colaboram para posição de destaque do agronegócio brasileiro. Conforme dados do United States Department of Agriculture (USDA, 2016), o Brasil é o segundo maior produtor e ocupa a posição de primeiro exportador do grão, superando os Estados Unidos desde a safra 2012/13, o que evidencia o papel de destaque do Brasil como principal player no mercado internacional.

Entre os estados brasileiros, o Estado do Mato Grosso é o principal produtor de soja, mas, em contraste a sua grande produção, o estado por esta localizado no Centro-Oeste brasileiro, demanda de um longo processo logístico para escoar a produção até os portos.

Além disso, o grão segue para os portos brasileiros basicamente através do modal rodoviário, sendo este o modal que apresenta um maior custo e menor eficiência (em termos de capacidade movimentada) para o transporte de carga desse gênero (PINHEIRO E CAIXETA-FILHO, 2009).

Analisando a condição da logística brasileira e a necessidade de elevar a competitividade da soja, alguns trabalhos se dedicam a desenvolver estudos para determinar as rotas ótimas da soja com origem na propriedade rural até os portos de exportação e, consequentemente, diminuir os custos logísticos.

Ferrari (2006) busca organizar o arranjo espacial das unidades armazenadoras de soja no estado do Mato Grosso e o dimensionamento destes armazéns com o objetivo de minimizar os custos de transporte, de armazenamento e de distribuição até os principais portos. Oliveira (2007) apresenta uma formulação linear e estima os fluxos nas principais alternativas de rotas de exportação da soja no estado do Mato Grosso que implicam em menor custo de escoamento. Oliveira e Yamakami (2006) analisou a distribuição logística da soja brasileira aplicando-se um modelo de equilíbrio espacial de programação quadrática propondo uma nova reconfiguração do transporte. Pinheiro e Caixeta-Filho (2009) propõem um modelo linear para avaliar o custo de transporte rodoviário de levar a soja das microrregiões mato-grossense para o porto de Paranaguá e de Itaqui como alternativa para o despacho de carga pelo Porto de Santos. Dubke e Pizzolato (2011) tratam o problema de escoamento de soja desenvolvendo um modelo de localização capacitado para terminais especializados usando o modelo tradicional de transporte combinado com multi-commodity e fluxo de redes para multi-facilidades. Amaral, Almeida e Morabito (2012) ressaltam a importância de rotas intermodais nos casos de produtos agrícolas destinados a exportação. Assim, os autores propõem um modelo de localização de facilidades p-mediana para localização de terminais intermodais utilizando os principais corredores usados para exportação da soja. Peixoto e Pinto (2012) apresentam três modelos de rede de fluxo da soja entre as áreas produtoras e as processadoras. O primeiro modelo considera que o grão é transportado entre os pontos de origem e destino, no segundo modelo é possível o transporte direto e a passagem do grão por pelo menos dois pontos de transbordo e no terceiro por pelo menos um ponto de transbordo.

Neste contexto, este trabalho propõe a concepção da rede pela localização de hubs, que através da consolidação de carga obtém vantagens de economia de escala reduzindo o custo de transporte e aumenta a eficiência da rede.

Inicialmente problema de localização de hubs destacou-se no uso de redes de hubs em sistemas de transporte e telecomunicações que atendem a demanda por produtos ou informação entre diversas origens e diversos destinos. Ao invés de servir a demanda de cada par origem-destino com uma ligação direta, hubs podem ser usados para redirecionar e consolidar fluxos entre origem e destino, que resulta em uma redução do número de ligações na rede e permite economia de escala pela conexão defluxo entre dois hubs. Como ponto de consolidação, fluxos com a mesma origem e destinos distintos são consolidados ou combinados com fluxos que têm origens distintas e mesmo destino.

O problema de localização de hubs aborda simultaneamente a localização de hubs e designação de nós de demanda a hubs, a fim de rotear o tráfego entre o par origem-destino. Existem dois tipos de redes de hubs, chamadas de alocação única e alocação múltipla, que diferem na forma de alocação de nós de demanda a hubs. Na rede de hubs com alocação única todo tráfego de entrada e saída de um nó de demanda é roteado por um único hub, enquanto na rede de hubs com alocação múltipla, o tráfego de entrada e saída de um nó de demanda pode ser roteado por um ou mais hubs. Além disso, hubs podem ter uma capacidade finita ou infinita do fluxo que pode ser recebido, transferido e distribuído.

Segundo Campbell (1994) o problema de localização discreta de hubs é classificando de acordo com a função objetivo: p-hub mediana, em que se minimiza o custo total de transporte, hub com custo fixo, que minimiza o custo total de transporte mais o custo fixo de abrir os hubs, p-hub centro, que minimiza o máximo tempo ou custo de transporte e o problema de cobertura por hubs, que minimiza o número de hubs abertos de forma que o tempo ou custo de transporte de fluxo entre qualquer origem e qualquer destino situa-se dentro de um limite.

Apesar do problema de localização de hub ter sido desenvolvido para solucionar o problema de transporte aéreo de passageiros e cargas recentemente, várias extensões do problema têm sido desenvolvidas. Kara e Tansel (2001) que tratam do problema de transporte carga onde, o tempo de chegada dos caminhões para consolidação nos hubs, o tempo de descarregar a carga, separá-la e a recarregar, influência diretamente no tempo de entrega. Assim, os autores propõem o problema The latest arrival hub location problem, onde o tempo transitório da carga é incorporado ao problema. Yaman et al, (2007) propõem um modelo de hub centro que considera o tempo de chegada no hub e incorpora múltiplas paradas e roteamento de veículos. E ainda, destaca-se a investigação de casos de redes de hubs aplicados a transporte marítimo e ferroviário, respectivamente, pelos autores Aversa et al. (2005) e Jeong et al. (2007). Aykin (1994) apresenta um modelo capacitado de rede de hubs onde o transporte direto entre nós não-hubs é permitido. Alumur e Kara (2008) apresentam uma revisão de modelos de localização de hubs e mais extensões.

Neste trabalho é proposto o modelo capacitado de localização de hub com custo fixo e alocação múltipla (CMAHLP) para tratar do problema de escoamento da soja do estado do Mato Grosso (MT) até o porto, de onde a soja é exportada. O foco principal é determinar as localizações estratégicas para o escoamento, instalando hubs para consolidação e/ou mudança de modal, com o propósito de diminuir os custos e tornar a rede mais eficiente. Para aproximar o modelo matemático do cenário real de exportação, este artigo propõe 3 extensões do modelo CMAHLP: o modelo CMAHLP-D, que permite ligações diretas entre as origens-destinos, CMAHLP-R, que dados a carga disponível da soja e quantidade requerida, o modelo roteia a carga de modo a atender a demanda e CMAHLP-RD, que permite a ligação direta entre origens-destinos do modelo CMAHLP-R. Outra medida adotada, para aproximar o modelo da realidade, foi considerar que o investimento destinado a abertura de hubs é analisado de dois modos, quando o investimento é pago integralmente no início da operação e quando este investimento é financiado e o valor pago por operação é a parcela deste investimento.

A seguir a seção dois apresenta uma descrição do problema, descrevendo os dados utilizados e os modelos propostos. A seção três descreve os resultados computacionais que discute os resultados obtidos em cada modelo e na seção quatro abordamos as principais conclusões e uma análise geral.

2. Descrição do Problema

As grandes dimensões do Estado do Mato Grosso e a complexidade econômica tornam necessária a divisão do mesmo para facilitar os levantamentos de dados e dimensionar a sua economia agropecuária (IMEA, 2013). A divisão territorial adotada é a realizada pelo IBGE, que considera 22 microrregiões. Em função desta subdivisão, foi estimado um quadro de Balanço de Oferta e Demanda (Tabela 1) para as microrregiões para a safra 2012, isto porque as estatísticas oficiais não dispõem destas informações para o nível desagregado de microrregião. O objetivo destas estimativas foi dimensionar o volume disponível para exportação das diferentes microrregiões. Em função da participação relativa de cada microrregião na produção [5], a estimativa de exportação por microrregião seguiu o mesmo comportamento da participação relativa na produção. Ou seja, a microrregião de Alto Teles Pires teve uma participação relativa na produção de 35%, considerando-se as exportações de soja do Estado do Mato Grosso em 2012 que totalizaram 10.763,29 mil toneladas [6], a exportação estimada de Alto Teles Pires foi de 3.767,56 mil toneladas, o que corresponde também a uma participação de 35% nas exportações.

Tabela 1. Oferta e Demanda de soja, Microrregiões do Estado do Mato Grosso, 2012 (mil toneladas)

Fonte: Dados da pesquisa, 2014

Para decidir os portos que seriam considerados, foi realizado um levantamento do volume movimentado pelos portos brasileiros entre 2008-2012 a partir dos dados do Sistema de Análise das Informações de Comércio Exterior (AliceWeb) da Secretaria de Comércio Exterior, do Ministério do Desenvolvimento, Indústria e Comércio Exterior (BRASIL, 2013), e assim, selecionados os portos que foram significativos para a exportação da soja. Os portos que ocasionalmente são utilizados para o escoamento foram descartados e seus fluxos contabilizados aos portos mais próximos. Logo, os portos selecionados são: Manaus (AM), Santarém (PA), São Luís (MA), Vitória (ES), Santos (SP), Porto de Paranaguá (PR) e São Francisco do Sul (SC).

A Figura 1 apresenta o Estado do Mato Grosso e a produção de soja por microrregião. Também estão representados os portos e pontos de transbordo utilizados, assim como, as rotas descritas.

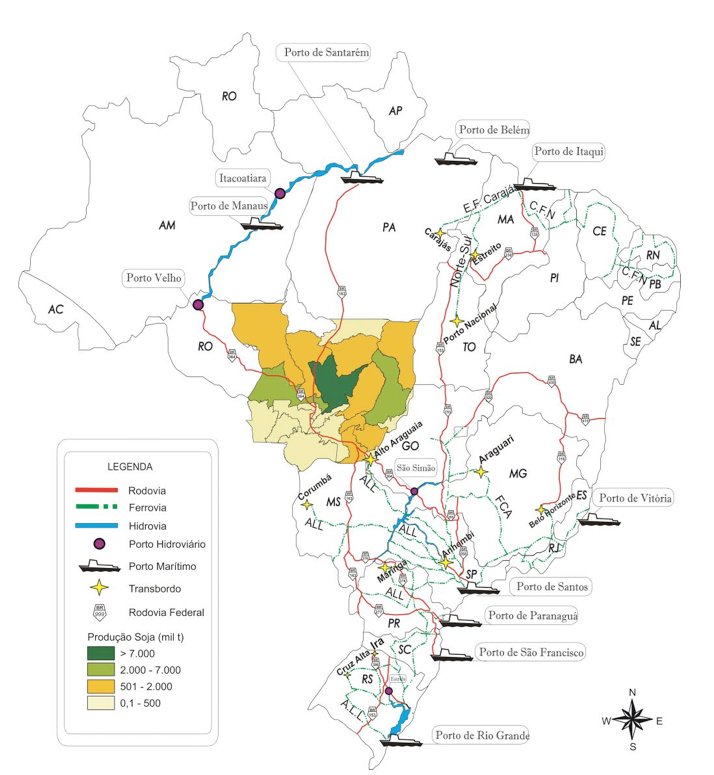
Figura 1. Principais rotas de transporte da soja mato-grossense.
Fonte: Elaborado pelos autores baseado em Oliveira (2014)

Os dados referentes à quantidade de soja destinada a cada porto tiveram como fonte dados Sistema Aliceweb (BRASIL, 2013), estes valores são apresentados na Tabela 2. Além das informações de soja disponível para exportação e a quantidade de soja escoada porcada porto, também foi realizado um levantamento das rotas de movimentação para exportação, unimodais e intermodais.

Tabela 2. Quantidade exportada de soja do Estado do Mato Grosso por porto, 2012 (mil toneladas)

Fonte: BRASIL (2013)

Com base nas distâncias percorridas pela carga e pelo modal utilizado foi realizado um levantamento do frete cobrado por cada modal, em US$/tonelada, as tarifas cobradas nos terminais de transbordo e as tarifas portuárias. O resultado são os custos cobrados para as rotas de escoamento e respectivas possibilidades de composições modais.

Para tratar o problema é proposto o modelo CMAHLP, apresentado por Ebery (2000):

Tabela 3. Capacidade e custo de instalação de hubs para cada nó da rede

Além das 22 microrregiões que compõe o estado do Mato Grosso, os pontos de intermodalidade também são considerados nós da rede e, são eles: Porto Velho (RO), São Simão (GO), Araguari (MG), Maringá (PR), Porto Nacional (TO). Considerando as localidades onde é possível a troca de modais é necessário destacar que a microrregião 3-Alto Araguaia (MT).

As informações da Tabela 3 sugerem as rotas praticadas na movimentação da soja. A principal delas é a movimentação via Alto Araguaia (MT) até o Porto de Santos. A soja parte das diferentes regiões produtoras por caminhão com destino ao Terminal Ferroviário de Alto Araguaia, na região sudeste do Estado. Deste terminal embarcam na ferrovia e seguem até o Porto de Santos. Outra rota possível e praticada é a movimentação via Porto Velho (RO) até os portos de Manaus e Santarém. A soja segue de caminhão até o Terminal Hidroviário de Santarém que é então carregada nas barcaças e segue até os portos de Manaus e Santarém por hidrovia. Hidrovia do Madeira. Outra rota considerada foi uma rota futura, em função dos novos projetos de infraestrutura desenhados pelo Governo Federal. Dentre elas, destaca-se a rota via Porto Nacional (TO). A soja seguiria de caminhão até o Terminal Ferroviário de Porto Nacional e depois, via ferrovia, até o Porto de São Luís (MA).

Na eq. (1) é descrita a função objetivo do problema, que minimiza o transporte do fluxo de carga da origem até seu destino final e o custo da abertura de hubs. A eq. (2) representa a conservação de fluxo do nó de origem i que pode ser alocado a mais de um hub, no entanto, o fluxo total que sai de i e é destinado a diferentes hubs deve ser igual a todo fluxo que sai de i. A eq. (3) é conservação de fluxo do no destino j, o fluxo que sai de i com destino a j pode passar por diferentes hubs, mas a quantidade desse fluxo sempre deve ser igual à quantidade de fluxo de i para j. A eq. (4) é a conservação nos hubs, todo fluxo que entra em um hub k, que tem origem no nó i não-hub ou de origem de outro hub l, e tudo que sai deste hub, com destino ao nó não-hub j ou a outro hub l, deve ser igual a zero. Na eq. (5) a soma de todo o fluxo destinado ao hub k não pode exceder a sua capacidade.  As eq. (6) e (7) garantem que não há fluxo direto entre nós não-hubs e as eq. (8) e (9) definem as variáveis contínuas e binárias, respectivamente.

Na função objetivo do problema (eq. 10) é adicionado o termo que representa o fluxo direto, a eq. 11 é a conservação de fluxos em cada nó i, a eq. 12 é a conservação de fluxos no nó j, a eq. 13 e a 14 garantem que o fluxo direto entre a origem i e o destino j só é permitida se i e j não são hubs e a eq. 15 define as variáveis contínuas.

Na segunda extensão, o trabalho propõe uma comparação entre rotear um fluxo pré-definido entre origem-destino (Wij)  do modelo CMAHLP e permitir que o próprio modelo matemático decida a quantidade da carga que deve sair de cada origem para atender as demandas, criando o modelo CMAHLP-R.

A formulação matemática do modelo CMAHLP-R é dada por:

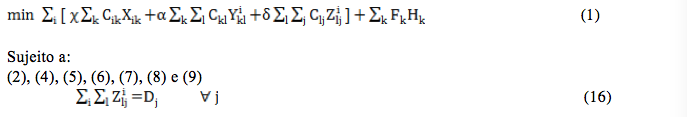
A eq. 16 garante que a demanda do nó j é atendida, no entanto, a origem do fluxo não é definida.
E a terceira extensão, é uma variação do modelo CMAHLP-D para que este modelo também roteie o fluxo. Esta extensão é denominada CMAHLP-DR e, sua formulação matemática é:

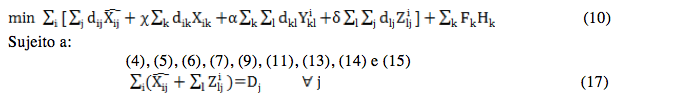
A eq. 17 garante que a demanda do nó j é atendida por fluxo direto entre origem-destino ou roteado por hubs e, a origem do fluxo é definida pelo modelo.

3. Resultados e Discussão

De acordo com a formulação matemática do problema CMAHLP e CMAHLP-D é necessário conhecer a quantidade que carga que sai de uma origem para determinado destino (  e os dados do problema fornecem apenas a quantidade disponível na origem e a quantidade requerida pela demanda.

Para solucionar este problema e definir as quantidades especificas entre as origens-destinos foi utilizado o problema de fluxos em redes com o objetivo de minimizar o custo de transporte {min z= cx: Ax=b,0 ≤ x ≤ ∞}, onde, c é o vetor de custos nos arcos, x é o vetor de fluxos nos arcos, A é a matriz de incidência nó-arco e b é o vetor demanda nos nós.

O resultado obtido pelo problema de fluxos em redes é apresentado na Tabela 4, que representada apenas as origens com soja disponível para exportação.

Tabela 4. Matriz de fluxos (W_ij) em toneladas

Os problemas propostos foram implementados em CPLEX 12.4 e os testes realizados em um computador i3 2.20GHz de 4GB em sistema operacional Ubuntu 11.04.

As Tabelas 5 a 11 apresentam as análises dos resultados computacionais. A primeira coluna indica o número de hubs abertos, a segunda, o custo total de transportar a carga e abrir os hubs, a terceira as localizações onde os hubs são abertos, a quarta, o quanto é utilizado apenas para abertura dos hubs e a quinta, o custo de transporte da carga dada a abertura dos hubs.

A Tabela 5 apresenta os resultados obtidos para o modelo CMAHLP considerando que o investimento para abertura dos hubs é pago integralmente no início da operação.

Tabela 5. Modelo CMAHLP com pagamento integral no 1° período

Observe que, considerando o investimento total a ser realizado, o modelo sugere a abertura de 16 hubs, o que significa investir US$ 526 milhões na abertura de hubs. O roteamento dos fluxos através deste conjunto de hubs abertos implica em um custo de transporte de US$ 1.157 milhões, e um custo total de US$ 1.684 milhões.

Os resultados são aderentes ao contexto real da demanda logística da soja mato-grossense. Se tomarmos o exemplo de Alto Araguaia, este é caracterizado como um importante ponto de transbordo ferroviário, que compõe uma das principais opções logísticas para a exportação da soja, assim o hub é necessário e justificado. Da mesma forma, para as regiões de São Simão, Maringá, Porto Velho e Porto Nacional, importantes terminais de transbordo ferroviário e hidroviário, que caso alcancem um nível adequado de armazenagem, podem ampliar as movimentações, implicando numa redução dos custos logísticos em função dos ganhos com a intermodalidade com a prática dessas rotas. Já regiões como Paranatinga e Tesouro, importantes produtoras, detêm altos índices de déficit de armazenagem, o que explica a abertura dos hubs.

Ao realizar uma análise em torno do número ótimo de hubs, fica evidente que neste caso, aumentar o número de hubs abertos não beneficia o transporte. É possível que haja uma configuração com um número maior de hubs que beneficie mais o transporte, mas esta configuração se distanciaria de modo mais significativo em termos de custo total e da proposta de análise do trade off entre o custo total e o custo de transporte.

Considerando que o investimento para abertura de hubs não é realizado integralmente no momento do início da operação, mas sim, que este investimento é normalmente financiado a uma taxa de juros e, o pagamento desse financiamento é realizado em um horizonte de tempo, a Tabela 6 mostra o impacto do parcelamento da abertura dos hubs no planejamento da rede.

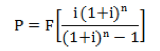
Tabela 6. Modelo CMAHLP com pagamento anual do investimento

O valor ótimo de investimento resultante do modelo para a abertura de hubs com financiamento é de 17 hubs a um custo total de US$ 1.243 milhões onde, destes US$ 85 milhões são utilizados para pagar a parte de infraestrutura e US$ 1.157 milhões para o pagamento do transporte.

Comparando a Tabela 5 e a Tabela 6 é possível observar que para 17 hubs (Tabela 6) o modelo realiza escolhas distintas de localizações para abertura de hubs quando comparado às localidades escolhidas para 17 hubs (Tabela 5) e resulta num custo menor de transporte. No entanto, neste caso, o menor custo de transporte é obtido para configuração de rede com 18 hubs, que implica num aumento de US$ 100 mil no custo total.

Os resultados para o CMAHLP-D. tanto para pagamento integral do investimento como no caso do financiamento, evidencia a importância de trabalhar o problema multi-períodos. No caso do pagamento integral do investimento, o modelo indicou a abertura de um único hub, na localidade 27, pois este viabiliza a rota intermodal com destino ao porto de São Luís, e as demais entregas são realizadas através de ligação direta a um custo total de US$ 1.183.680.00-, um custo de abertura de hubs de US$ 45.000.00- e um custo de transporte de US$ 1.138.680.00-. Este resultado é justificado pelo fato do investimento para abertura de hub ser alto e superar a economia de escala no transporte.

Agora, ao considerar que o investimento é financiado, o modelo abre 5 hubs (Tabela 7) um número significativamente menor do que os 17 hubs abertos pelo modelo CMAHLP com pagamento anual (Tabela 6) e ainda resulta em economia no custo de transporte e custo total quando comparado aos custos para 17 hubs.

Tabela 7. Modelo CMAHLP-D com pagamento anual do investimento

Os resultados do modelo CMAHLP-R (Tabela 8) permitem uma comparação direta entre as vantagens de trabalhar na rede com os fluxos pré-definidos (Tabela 5) e de permitir que o modelo roteie o fluxo de modo a minimizar os custos.

Tabela 8. Modelo CMAHLP–R com pagamento integral no 1° período

Para o pagamento integral do investimento, o modelo CMAHLP-R abre hubs em 9 localidades a um custo total de US$ 1.668 milhões, enquanto que para o fluxo pré-definido são abertos 16 hubs a um custo total de US$ 1.684 milhões. No entanto, o fator mais expressivo da flexibilidade do fluxo é expresso pelo custo de transporte, onde a economia é de aproximadamente US$ 7 milhões, mesmo com a redução do número de hubs, quando a mesma comparação é feita para 9 hubs abertos para o modelo CMAHLP o impacto econômico se torna mais evidente. Os custos em investimento de infraestrutura e as localidades escolhidas para instalação de hubs, neste caso, são os mesmos, no entanto, o modelo CMAHLP-R resulta em uma economia de aproximadamente US$ 20 milhões no custo total, resultado da economia obtida pelo custo de transporte.

A análise do trade off mostra que para 16 hubs abertos, a um investimento total a mais de US$ 260 mil, obtém-se uma economia em transporte de aproximadamente US$ 8 milhões. Ao comparar a abertura de 16 hubs do modelo CMAHLP e CMAHLP-R (Tabelas 5 e 8, respectivamente), observa-se que a economia obtida pelo CMAHLP-R é de aproximadamente US$ 16 milhões.

A Tabela 9 apresenta os resultados do modelo CMAHLP-R considerando o pagamento anual do investimento e a melhora obtida em termos de custos é muito expressiva quando comparado ao resultado CMAHLP para pagamento anual do investimento. O modelo CMAHLP-R abre 16 hubs enquanto o modelo CMAHLP abre 17, no entanto, a diferença em termos de custo total é de mais de US$ 100 milhões e, esta diferença é, em sua maioria, reflexo da economia obtida pelo transporte.

Tabela 9. Modelo CMAHLP-R com pagamento anual do investimento

Já análise do trade off, neste caso, mostra que o resultado ótimo é a melhor opção, pois o menor custo de transporte é o do resultado ótimo e a redução no custo de investimento resulta em um custo total elevado.

A análise dos resultados do modelo CMAHLP-RD é semelhante a análise do modelo CMAHLP-D.

Para o pagamento integral do investimento no 1° período obtêm-se um custo total de US$ 1.183.680.00-, um custo de abertura de hubs de US$ 45.000.00- e um custo de transporte de US$ 1.138.680.00-. O mais importante a ser destacado nestes resultados é o valor ótimo apresentado na Tabela 10, que obteve o menor custo total, reflexo do menor custo de transporte, quando comparado com todas as análises realizadas para os modelos anteriores.

Tabela 10. Modelo CMAHLP-RD com pagamento anual do investimento

A análise do trade off dos resultados da Tabela 10 também não apresenta opções significativas para tomada de decisão pois, o menor custo de transporte é o custo do resultado ótimo e o menor custo de investimento causa um aumento de aproximadamente US$ 500 mil do custo total e um aumento de aproximadamente US$ 1 milhão do custo de transporte, o que não seria vantajoso no longo prazo.

4. Conclusão

O modelo proposto por este trabalho para rotear a soja destinada para exportação foi o modelo CMAHLP, que abre os hubs e roteia os fluxos de forma a minimizar o custo total, isto não implica necessariamente em minimizar o custo de abertura de hubs e/ou custo de transporte.

No intuito de melhor descrever o problema real foram propostos3 extensões do problema: CMAHLP-D. CMAHLP-R e CMAHLP-RD. além da análise dos 4 modelos no caso em que o investimento em infraestrutura é pago dentro de um horizonte de tempo.

A comparação dos resultados obtidos pelos modelos CMAHLP e CMAHLP-R permite afirmar que a liberdade do modelo rotear o fluxo resulta em melhores resultados e se mostra mais adequado para o sistema. Já ao considerar os prazos para o pagamento dos hubs causa reflexo positivo na escolha de hubs e no resultado obtido pelos modelos. Porém, este trabalho considera um único período de tempo, o permite a conclusão de que ao considerar um número maior de períodos, o resultado obtido não corresponderá à realidade, sendo insuficiente para escoar a soja. 

Referências Bibliográficas

ALUMUR.S.; KARA. B. Y. (2008). Network hub location problems: The state of the art. European Journal of Operational Research. v.190. n.1, p.1-21.

AMARAL.M.; ALMEIDA.M.S.; MORABITO. R. (2012). Um modelo fluxos e localização de terminais intermodais para escoamento da soja brasileira destinada à exportação. Gestão e Produção, v.19, n.2, p.717-732.

AVERSA. R.; BOTTER.H.E.; HARALAMBIDES.R.C.; YOSHIZAKI.H.T.Y. (2005). A mixed integer programming model on the location of a hub port in the east coast of South America. Maritime Economics and Logistics, v.7, n.1, p.1-18.

AYKIN. T. (1994). Lagrangian relaxation based approaches to capacitated hub-and-spoke network design problem. European Journal of Operational Research. v.79. n.3, p.501-523.

BRASIL (2013). MDIC. Ministério do Desenvolvimento, Indústria e Comércio Exterior. Estatísticas do Comércio Exterior - Sistema de Análise das Informações de Comércio Exterior (AliceWeb). Disponível em: <http://aliceweb.desenvolvimento.gov.br/>. Acesso em: dez. 2013

CAMPBELL.J. F. (1994). Integer programming formulations of discrete hub location problems. European Journal of Operational Research. v.72, n.2, p.387-405.

DUBKE. A. F.; PIZZOLATO. N. D. (2011). Location model of specialized terminals for soybean exports in Brazil. Pesquisa Operacional. v.31, n.1, p.21-40.

EBERY.J.; KRISHNAMOORTHY.M.. ERNST.A.; BOLAND. N. (2000). The capacitated multiple allocation hub location problem: Formulations and algorithms. European Journal of Operational Research. v.120, n.3, p. 614-631.

IMEA (2013). Instituto Mato-grossense de Economia Agropecuária. Mapa das regiões. Disponível em: http://www.imea.com.br/upload/publicacoes/arquivos/justificativamapa.pdf

JEONG.S.J.; LEE.C.G.; BOOKBINDER.J.H. (2007). The European freight railway system as a hub-and-spoke network. Transportation Research Part A. v.41. n.6, p.523-536.

KARA, B.Y.; TANSEL, B.C. (2001). The latest arrival hub location problem. Management Science, v.47, n.10, p.1408-1420.

PINHEIRO. M. A.; CAIXETA-FILHO. J. V. (2009). O escoamento da soja em grão do Mato Grosso para exportação pelos portos de Santos. Paranaguá e Itaqui: uma aplicação de programação linear. Sociedade Brasileira de economia Administração e Sociologia Rural - SOBER. 2009. 19p.

FERRARI. R. C. Utilização de modelo matemático de otimização para identificação de locais para instalação de unidades armazenadoras de soja no estado de Mato Grosso. Piracicaba. 2006. 185p. Dissertação de Mestrado – Escola Superior de Agronomia “Luiz de Queiroz”. Universidade de São Paulo.

OLIVEIRA. A. L. R. (2007). Transporte de soja do Estado do Mato Grosso para exportação: uma aplicação de programação linear. Revista de Economia Agrícola, v.54, n.1, p. 33-41.

OLIVEIRA, A. L. R. (2014). A logística do agronegócio: para além do apagão logístico. In: Buainain, A. M.; ALVES, E.; SILVEIRA, J. M. F. J.; NAVARRO, Z. (Org.). O mundo rural no Brasil do século 21: a formação de um novo padrão agrário e agrícola. 1ed. Brasília: Embrapa, v.1, p.337-370.

OLIVEIRA, A. L. R.; SILVEIRA, J. M. F. J. (2013). Restructuring of the corn supply chain in Brazil: facing the challenges in logistics or regulation of biotechnology. The International Food and Agribusiness Management Review, v.16, n.4, p. 1-24.

OLIVEIRA, A. L. R.; YAMAKAMI, A. (2006) Modelo de programação quadrática para análise da movimentação logística e comercialização da soja brasileira. Engenharia Agrícola, v.26, n.2, p.552-560.

PEIXOTO. N. E. S.; PINTO. K. C. R. (2012). Rede de fluxo de custo mínimo para a soja destinada ao processamento no centro- sudeste brasileiro. Simpósio de Pesquisa Operacional & Logística da Mainha. 2012.

THUESEN. G. J.; FABRYCKY.W. J. (2001). Engineering economy.9th ed. Englewood Cliffs: Prentice-Hall. 637p.

USDA (2016). United States Department of Agriculture. Commodities and Products. Disponível em: <http://www.fas.usda.gov/commodities>. Acesso em: mai.2016.

YAMAN.H.; KARA.B.Y.; TANSEL.B.C. The latest arrival hub location problem for cargo delivery systems with stopovers. Transportation Research Part B. v.41, n.8, p.906-919.

1. Faculdade de Engenharia Elétrica e de Computação, Universidade de Campinas (UNICAMP), Brasil. Email: apmilanez@gmail.com
2. Faculdade de Engenharia Agrícola, Universidade de Campinas (UNICAMP), Brasil. Email: andrea.oliveira@feagri.unicamp.br
3. Faculdade de Ciências Aplicadas, Universidade de Campinas (UNICAMP), Brasil. Email: anibal.azevedo@fca.unicamp.br

4. Faculdade de Engenharia Elétrica e de Computação, Universidade de Campinas (UNICAMP), Brasil. Email: taka@densis.fee.unicamp.br

5. A produção considerada foi de 21.978,34 mil toneladas que desconta o volume das regiões “demandantes” de soja, ou seja, tem maior capacidade de processamento e não dispõem de soja para exportação, uma vez que consomem toda sua produção. Assim, desconsideraram-se as microrregiões de Alto Araguaia, Cuiabá e Rondonópolis para computar a participação relativa.

6. Conforme dados oficiais do Ministério do Desenvolvimento, Indústria e Comércio Exterior (BRASIL, 2013).