HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 34) Año 2016. Pág. 9

Balanceo de Líneas de Ensamble en U considerando riesgos Ergonómicos

U-shaped assembly line balancing problem with ergonomic risks constraint

Jairo R. CORONADO-HERNÁNDEZ 1; Holman OSPINA-MATEUS 2

Recibido: 18/06/16 • Aprobado: 12/07/2016

Contenido

1. Introducción

2. Métodos de Valoración de Riesgos Ergonómicos

3. Balanceo de Línea de Ensamble en U

4. Balanceo de línea en U considerando riesgos ergonómicos

5. Validación de Balanceo de Línea en U Considerando Riesgos Ergonómicos (Ergo-UALBP-C)

6. Conclusiones

Referencias

1. Introducción

El propósito de este trabajo es la incorporación de riesgos ergonómicos dentro de las líneas de ensamble en U, donde se busca el aprovechamiento de la fuerza de trabajo motivado en filosofías como el Lean Manufacturing y JIT (Aase, Olson, & Schniederjans, 2004). Las consideraciones ergonómicas son muy importantes en el diseño y planificación de operaciones, puesto que en el mundo laboral es común encontrar que las condiciones del trabajo no generan confort, ni bienestar en los trabajadores. De hecho, existe una concepción errónea donde el empleado se debe adaptar al trabajo, y no el trabajo al ser humano (Mondelo, Torada, & Bombardo, 2010). La ergonomía busca la optimización del bienestar humano dentro de los sistemas organizacionales. Por ello, la implementación de soluciones ergonómicas debe comenzar con una modificación del puesto del trabajo y una aplicación de técnicas para la organización y programación de actividades  (Ferguson, Marras, Gary Allread, Knapik, & Splittstoesser, 2012).

Dentro de problemas más comunes por no tener puestos de trabajos ergonómicos se encuentran los  Trastornos Musculo Esqueléticos (TME). Este,  se define como el conjunto de afecciones de los músculos, huesos, tendones y nervios que dependen en gran medida a los niveles de exposición ocupacionales (intensidad, frecuencia y duración) en factores biomecánicos (movimientos repetitivos, manipulación de carga, esfuerzos extenuantes, posturas incomodas), factores psicosociales (estrés, carga mental, ansiedad, desesperación, relaciones interpersonales, organización, funcionalidad, temporalidad, autonomía, monotonía) y factores individuales (edad, genero, antropometría, hábitos, actividad física, contextura, patrones genéticos) (Bernard & Putz-Anderson, 1997). Los trabajadores se encuentran propensos al desarrollo de trastornos musculo esqueléticos, debido a condiciones riesgosas y desfavorables en la dinámica de actividades y operaciones dentro de los puestos de trabajo. Las afecciones, incapacidades, absentismo laboral y enfermedades profesionales, muestran la presencia de trastornos musculo esqueléticos, que pone en riesgo la salud y calidad de vida de los trabajadores, y tiene un alto costo para las organizaciones (B J Carnahan & Redfern, 1998). 

Los trastornos musculo esqueléticos afectan principalmente en los miembros superiores, dentro de la información más completa en la actualidad recopilada por académicos existe una lista de las 12 desordenes musculo esqueléticos en los miembros superiores, así: Dolor en Cuello, Síndrome del Manguito Rotador, Epicondilitis Media y Lateral, Atrapamiento del Nervio Cubital, Atrapamiento del Nervio Radial, Tendinitis, Enfermedad de Quervain, Síndrome del Túnel Carpiano, Síndrome del Canal de Guyón, Fenómeno de Raynaud, Vibración de Mano y Brazo, y Trastornos Musculo Esqueléticos de Miembros Superiores No Especificado (Aptel, Aublet-Cuvelier, & Cnockaert, 2002). En (Otto & Scholl, 2011), se ha mostrado que el balanceo de línea puede ser adoptado como una estrategia efectiva en el corto plazo cuando se hallan riesgos ergonómicos.

La aplicación de aspectos ergonómicos en las líneas de ensamble ha sido tratada por diversos autores. Encontramos el trabajo desarrollado por Carnahan et al 2001, quien  incorporo la demanda física en la asignación de las tareas cuando se manipula carga, optimizando los riesgos de los trabajadores y balanceo de la línea. En Miralles et al. 2008 y Costa & Miralles, 2009, se analizara un problema de asignación y rotación laboral de los trabajadores donde se permite la inclusión de trabajadores con discapacidad en una línea de ensamble. En Otto & Scholl, 2011, se analizará un problema de balanceo de línea considerando la inclusión de riesgos laborales. En Rajabalipour et al . 2012, se plantea un nuevo modelo de balanceo de línea considerando las posturas del trabajador, permitiendo la variaciones regulares de las tareas desarrolladas en las estaciones de trabajo. En Xu et al. 2012, se estudia la asignación de trabajadores integrando aspectos ergonómicos y productivos en el diseño de líneas de ensamble. En Battini et al. 2011, se analiza un modelo de balanceo de línea que introduce el gasto energético, como mecanismo de estimación de niveles ergonómicos. Recientes investigaciones de autores (Battini, Delorme, Dolgui, & Sgarbossa, 2015; Kazmierczak, Winkel, & Westgaard, 2004; Otto, 2014; Valhondo, 2013) han demostrado un impacto en la productividad y la ergonomía en los sistemas de ensamble al introducción nuevas restricciones y funciones objetivos con enfoque ergonómico. Estos estudios han sido soportado en el análisis con métodos de evaluación ergonómicos tradicionales (métodos indirectos-observación).

El presente documento está distribuido así: Sección 2 describe los diferentes métodos de valoración ergonómicas; la sección 3 define el modelo de balanceo de línea en U; la sección 4 considera el modelo de balanceo de línea en U tomando en cuenta riesgos ergonómicos; en la sección 5 se valida el modelo a través de un ejemplo práctico, y finalmente las conclusiones y perspectivas del problema son descritas en la última sección.

2. Métodos de Valoración de Riesgos Ergonómicos

Los métodos de valoración de riesgos ergonómicos sirven para determinar el nivel de riesgo al que están expuestos los trabajadores. Los métodos se basan entre otros en los movimientos repetitivos, la manipulación de carga y las posturas forzadas. Existen diversos métodos entre los que se tienen:

1. Método JSI (Job Strain Índex) (Steven Moore & Garg, 1995)
2. Método OCRA y Check List OCRA (Occhipinti & Colombini, 2005)
3. El método Sue Rodgers (Rodgers, 1992)
4. El método generalizado en la industria automovilística de europea (EAW) (Schaub, Caragnano, Britzke, & Bruder, 2013)
5. Método RULA ((McAtamney & Nigel Corlett, 1993)
6. Método OWAS (Karhu, Härkönen, Sorvali, & Vepsäläinen, 1981)
7. Ecuación NIOSH (Waters, Putz-Anderson, Garg, & Fine, 1993) y Tablas Snook y Ciriello (Snook & Ciriello, 1991).

En esta sección se hace énfasis en los métodos ergonómicos más conocidos en la valoración de riesgos ocupacionales, como lo muestran estudios desarrollados por Dempsey et al. (2005), David, (2005), y recomendaciones de normas Europea (EN, 2007). En la Tabla 1 se observan que factores de exposición miden los métodos de valoración de riesgos ocupacionales.

Tabla 1 . Factores de Exposición Evaluados por Diferentes Métodos, Adaptado de David (2005).

En este documento, ilustraremos un ejemplo práctico de una línea de ensamble en U. En la Figura 1 se observa el diagrama de precedencia y el Layout que diferencia una línea de ensamble tradicional y una línea de ensamble en U. El diagrama relaciona un conjunto de n = 12 tareas i =1, …,n ,que toman un tiempo ti en la ejecución de cada ensamble en la estación de trabajo, durante un tiempo de ciclo de c = 60 segundos. Cada actividad relaciona aspectos ergonómicos relacionados con las acciones (movimientos) y manipulación de carga, como se observa en la Tabla 2 . El objetivo es caracterizar el comportamiento natural de una línea de producción donde se requieren múltiples movimientos para ensamblar e incluir suministros que requieran carga y esfuerzo significativo por parte del trabajador.

Figura 1 . Representación del Balanceo de Línea, a) Diagrama de Precedencia;
b) Línea de Ensamble Tradicional. c) Distribución de Línea de Ensamble en U.

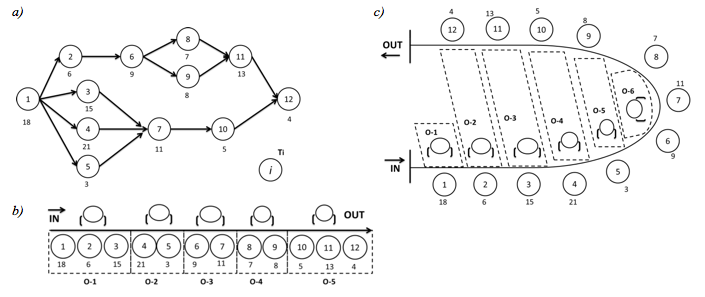
Tabla 2 . Ejemplo de Línea de Ensamble, Datos por Manipulación de Carga y Acciones.

Las tareas se distribuyen entre las estaciones de trabajo lo más suave posible de acuerdo con las relaciones de precedencia en el equilibrado de la línea de montaje. Sin embargo, así suavizar el tiempo total de la estación entre las estaciones puede ser sentido en muchas circunstancias industriales. En otras palabras, dos estaciones cuyos tiempos estación total son iguales pueden contener tareas con diferentes cargas ergonómicas. En consecuencia, sus grados de tensión pueden ser muy diferentes. Esta situación está subestimada en el equilibrio de la línea de montaje clásico, pero es un aspecto importante en la realidad. Sobre todo en las líneas de ensamblaje manual, donde el trabajo se realiza por parte del operador de forma repetitiva. Como resultado, hay un efecto acumulativo de fatiga en el trabajador. Líneas de montaje que no están bien diseñados ergonómicamente, no solo generan pérdida de productividad, sino también la generación de enfermedades profesionales en los trabajadores. Con el fin de prevenir estas complicaciones, el nivel de riesgo aceptable para una estación debe ser analizada y factores de riesgo ergonómicos de la estación debe ser analizada por encima de los nivel aceptables. El Índice OCRA, es un procedimiento muy eficiente para la evaluación del riesgo ergonómico que se explora en este estudio. Los parámetros del método se explican en detalle, y una comparación entre la línea y el montaje de diseño ergonómico y su impacto se presenta en sección 4.

2.1. Métodos de valoración ergonómica para la manipulación manual de carga: La ecuación Revisada de NIOSH (National Institute for Ocuppational)

La ecuación NIOSH  (Waters et al., 1993) ayuda a evaluar tareas de levantamiento de cargas, permitiendo obtener un peso máximo recomendado (RWL: Recommended Weight Limit) para manipular en el puesto de trabajo, evitando los sobresfuerzos y la aparición de lesiones en la espalda. La ecuación de NIOSH calcula el peso límite recomendado mediante fórmula 1. Donde: LC: Constante de Carga (23 o 25 Kg); FM: Factor Frecuencia.

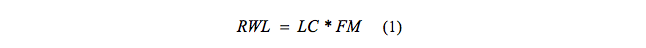
El método NIOSH arroja el Índice de levantamiento (IL), como el cociente entre el peso de la carga levantada y el límite de peso recomendado calculado para la tarea (ecuación 2). Dónde: LI es el índice de levantamiento; PC es el peso de la carga; RWL es el Peso Máximo Recomendado.

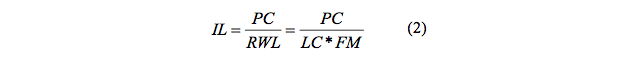
La frecuencia de manipulación de carga es la cantidad de maniobras o levantamientos ejercidos en el tiempo. El método NIOSH provee unos factores alineados a la frecuencia y duración de las actividades y la distancia vertical en centímetros en la que se desarrolla las operaciones como se muestra en la Tabla 3 .

Tabla 3 . Factor de Frecuencia de Tareas en la Ecuación NIOSH.

La ecuación NIOSH es interpretada de acuerdo a tres intervalos de riesgos. Cuando  la actividad no repercute un riesgo grave para los trabajadores.  la actividad es propensa a ocasionar problemas en los trabajadores.  la tarea ocasionará problemas en la salud de los trabajadores. En el desarrolla de un análisis multitarea NIOSH recomienda un Índice de Levantamiento Compuesto (ILc), así:

Tomando como referencia una constante de carga (LC) de 25 kg, calcularemos el riesgo del operador 6 en la línea de ensamble en U (Figura 1 .c) donde el trabajador es el encargado de desarrollar las tareas 6, 7 y 8 con un manipulación de carga de 12, 20 y 2 kilogramos respectivamente (Tabla 2 ). Dentro de las actividades realizadas en la línea de ensamble, la frecuencia de manipulación o levantamiento es equivalente a 1 por minuto, en relación con el tiempo de ciclo de 60 segundos. Considerando que la actividad es de larga duración el factor de frecuencia para 1, 2, 3 levantamiento por minuto es 0.75, 0,65 y 0.55 respectivamente. En la Tabla 4 se resumen los cálculos de riesgos independientes y de las tareas compuestas.

Tabla 4. Calculo de Riesgo por Manipulación de Carga Multitarea, Ejemplo Operador 6 en línea de ensamble U.

Los resultados evidencia de manera independiente riesgos leves que no superan el índice de 1,07 (Tarea 7), pero al ser valorada de manera integral todas las actividades del operador se obtiene un Índice de 1,23 que revela un nivel de riesgo moderado, y que muestra que el nivel de riesgo varía de acuerdo con las actividades desarrolladas por el operador 6 dentro de la estación laboral.

2.2. Métodos de valoración ergonómica para el análisis de repetitividad de actividades: Check List OCRA

El método Check List OCRA (ISO 11228-3:2007, n.d.; Occhipinti & Colombini, 2005) permite la evaluación de riesgos colectivos (frecuencia de acciones, posturas incomodas, movimiento de brazos, uso de fuerza, variación de posturas, periodos de recuperación) en función de la duración de las actividades. El método es calculado mediante la fórmula 4. Donde, FP Representa el Factor de Postura, FFrec Describe el Factor de Frecuencia, FFuerza es el Factor de Fuerza, FD expresa la influencia la duración de la tarea repetitiva.

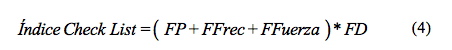
Los resultados del Índice Check List OCRA con valores inferiores a 5 son considerados en riesgo es óptimo. Para valores entre 5 y 7.5 el riesgo es aceptable. En índices entre 7.6 y 11 el riesgo es muy ligero. Entre 11.1 y 14 el riesgo es ligero. Entre 14.1 y 22.5 el riesgo es medio, y finalmente un índice superior a 22.5 es considerado un riesgo alto, el cual exige un seguimiento de las actividades del puesto de trabajo.

De acuerdo con el conjunto de tareas de la línea de ensamble (Tabla 2 ), se calcula el índice Check List OCRA para cada una de las tareas, considerando: i) el desarrollo de fuerza es moderada con una puntuación de 4; ii) Las actividades se realizan con los brazos extendidos y permanecen elevadas la mayoría del tiempo con puntuación de 1; iii) Las actividades se desarrolla en un rango de 7 a 8 horas con la necesidad de desarrollar actividades repetitivas, lo que genera un factor de duración de 1 ; iv) el factor de frecuencia es calculado por medio de la ecuación (FFrec = 0.214*(Acciones/Estación)-5.0389) que representa la regresión lineal de los valores establecidos por el método OCRA Check List (Figura 2 ). En la Tabla 4 se resumen los cálculos de riesgos por acciones repetitivas para cada una de las tareas. Por ejemplo en la actividad 6, contiene 27 acciones por minuto que hace referencia a un factor de frecuencia de 1, de esta manera el nivel de riesgo es igual a 5.74 ((0.7+1+4)*1).

Figura 2. Regresión Lineal de Acciones por Minuto en Puesto de Trabajo vs Puntuación OCRA Check List

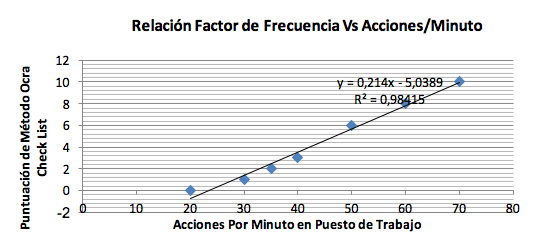
Para conocer el nivel de riesgos global en una estación de trabajo se acumulan la cantidad de acciones por minuto de las tareas en la estación de trabajo, y de esta manera se recalcula el nivel de riesgo con cada uno de los factores del método. En una estación de trabajo que contenga las tareas 8, 9 y 10 con 65 acciones por minutos, el nivel de riesgo se calcula modificando el factor de frecuencia, donde el método asigna un factor de 8.9, de esta manera el índice es igual a 14 ((8.9+1+4)*1), lo que muestra un índice medio que requiere un cuidado especial.

Tabla 5 . Calculo de Riesgo por Repetitividad de Acciones de Línea de Ensamble de Tabla 1

2.3. Supuestos Generales para el modelamiento de métodos de Valoración Ergonómicos

Luego de haber examinado varios métodos de valoración ergonómicos en aspectos como la manipulación de carga, la repetitividad de actividades y las posturas forzadas o incomodas, ahora formularemos las siguientes condiciones para la estimación de riesgos ergonómicos.

Además, se considera la función de estimación de riesgo ergonómicos F( ) es no decreciente y en muchos casos no lineal en los niveles de exposición.

Nota. Tomando en consideración que la no linealidad en los métodos de valoración ergonómica complican su inclusión dentro de un modelo de balanceo de línea en U, es importante y clave no omitirse, debido a que todos los métodos se fundamentan en funciones no lineales para la estimación del nivel de riesgo de acuerdo como lo señala Otto et al. (2011)

3. Balanceo de Línea de Ensamble en U

Una Línea de ensamble es un sistema de producción continua donde se busca la optimización de operaciones con estaciones de trabajo en serie. Originalmente, las líneas de ensamble fueron desarrolladas por su eficiencia en costos en la producción en masa de productos estandarizados. El ejemplo más famoso corresponde a la línea de ensamble desarrollada por Henrry Ford, donde se buscaba asignar operaciones en las estaciones de trabajo (Boysen, Fliedner, & Scholl, 2007). Una línea de ensamble, se constituye en un conjunto de estaciones de trabajo que se encuentra interrelacionado y conectado para el desarrollo de un conjunto de tareas y operaciones, que permiten el desarrollo de productos o bienes, y se caracteriza por poseer un tiempo de ciclo, y una distribución que permita establecer la misma carga de trabajo sobre las estaciones (John Miltenburg, 2001). Debido a una amplia variedad de esquemas para el balanceo de línea, se clasifica el problema de balanceo en ALBP (Assembly Line Balancing Problem), GALBP (General Assembly Line Balancing Problem), ALDP (Assembly Line Design Problem) y DLBP (Disassembly Line Balancing Problem). Bajo el esquema de GALBP (General Assembly Line Balancing Problem) y como lo señalan Miltenburg y Wijngaard (1994) así como Scholl y Klein (1999) se hallan los problemas de balanceo de líneas en U (UALBP), los cuales a su vez pueden ser clasificados en: i) UALBP-1: minimiza el número de estaciones dado un tiempo ciclo, ii) UALBP-2: minimiza el tiempo de ciclo, dado un número de estaciones y, iii) UALBP-E: maximiza la eficiencia de la línea. El Balanceo de Línea corresponde a una clase de problemas de optimización combinatoria considerados NP- hard. (Battaïa & Dolgui, 2013).

Una línea de producción en U, consiste en una línea de producción donde los topes de la línea están cerradas en cada extremo en forma de U. Las estaciones pueden trabajar en el mismo ciclo con dos o más piezas en diferentes posiciones de la línea. Hoy en día, muchas líneas de producción han introducido la utilización de líneas de ensamble en U, con el objetivo de potencializar la gestión productiva del ensamble bajo el uso de los principios de Justo a tiempo. Una de las características importantes que hacen una línea de montaje en forma de U diferentes de una línea de ensamble es que la entrada y la salida están en la misma posición (Yasuhiro Monden, 1983). Esto proporciona una rápida respuesta a los cambios del entorno debido a la posibilidad de reasignar los operadores cualificados, por lo tanto, aporta una mayor flexibilidad. La línea puede reequilibrarse fácilmente mediante la adición y eliminación de los trabajadores, por tanto, los cambios en las tasas de producción requeridos pueden ser adaptados fácilmente. (Hall, 1983; Yasuhiro Monden, 1983; Schonberger Richard, 1982) fueron los primero escritores en referenciar el uso de líneas de producción en U, en las compañías Japonesas. estos autores, identificaron las líneas en U como un tipo especial de celdas de manufactura utilizada en los sistemas de producción JIT (Just in Time). Estas cuestiones se discuten a fondo en Monden, (1995) en el contexto del Sistema de Producción Toyota, y las distintas técnicas consideradas en su optimización (Ohno & Nakade, 1997).

La implementación de una línea de balanceo en U permite mejorar la productividad, la calidad, el trabajo en equipo, el entrenamiento, la interacción y eficiencia del sistema (Aase et al., 2004; G. J. Miltenburg & Wijingaard, 1994). La alta participación de los trabajadores en las líneas en U aumenta la productividad en la medida que se realiza una gama más amplia de tareas. Cheng, Miltenburg, & Motwani, (2000), han enumerado diversos factores que relacionas las ventajas de las líneas en forma de U: flexibilidad en volumen de producción, flexibilidad en la operación, el número de estaciones de trabajo, manipulación de materiales, visibilidad y trabajo en equipo, minimización de reprocesos. 

El problema de balanceo de línea es introducido y modelo matemáticamente por primera vez por  Miltenburg & Wijingaard, (1994). El modelo UALBP es un sistema de producción que posee un número de tareas n, donde cada una de ella posee una relación de precedencia y unos tiempos de duración, Ti (i = 1,…,n), que son asignadas a una estación (j= 1,…,m). El objetivo de ULBP-1 es minimizar la cantidad de estaciones requeridas m*, para un tiempo de ciclo, C, de tal modo que:

Una de las principales características que UALBP es que debe permitir la asignación de las tareas en las estaciones de trabajo hacia adelante y hacia atrás (Por ejemplo la tarea inicial y final pueden estar en una misma estación en un sistema de ensamble en U), lo cual no se logra con un sistema de balanceo tradicional (Kriengkorakot & Pianthong, 2007). Para habilitar esta asignación que UALBP es necesaria la creación de una red “Fantasma” que sea agregada a la red original de precedencia (Jackson, 1956). En la Figura 3 , se ilustra la red de precedencia del ejemplo tabla 1 y figura 1, para un conjunto de 12 tareas con la red fantasma en líneas punteadas. Al iniciar en medio de la red extendida, se podrán desarrollar asignaciones en las estaciones hacia adelante por medio de la red original, hacia atrás a través de la red fantasma o simultáneamente en ambas direcciones.

Figura 3 . Red de precedencia de Figura 1 con red de Precedencia Fantasma.

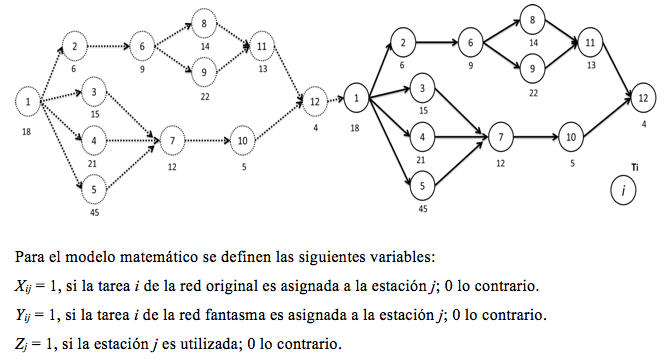
Además se define 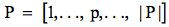que representa el conjunto de parejas ordenadas de tareas que reflejan relación de precedencia; de esta manera indica que la tarea r precede inmediatamente a la tarea s. De acuerdo con Urban (1998), El modelo de programación entera para el UABLP-1 es el siguiente:

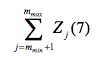
Minimizar

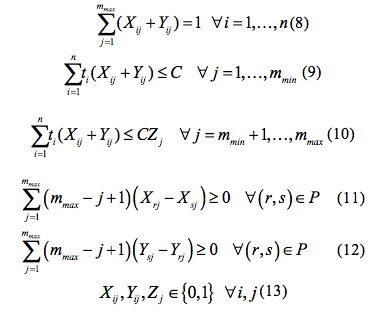
El objetivo de este modelo es minimizar la cantidad de estaciones, tomando como base las estaciones mínimas ya requeridas. La restricción (8) permite que cada tarea sea asignada a una sola estación de trabajo, y sea en la red original o fantasma. La restricción (9) y (10) asegura que la suma de las tareas asignadas en la estación de trabajo no exceda el tiempo de ciclo. Finalmente la restricción (11) y (12) relaciona la precedencia que existe en la red original y la red fantasma. Las variables binarias son definidas en la restricción (13).  Diversos autores han considerado una variedad de técnicas novedosas en la solución de problema de balanceo de línea entre las que se tiene la programación entera, dinámica, heurísticas y meta heurísticas, entre otras (Fattahi & Turkay, 2015; Hwang, Katayama, & Gen, 2008; J. Miltenburg & Sinnamon, 1995; Miralles et al., 2008; Scholl & Klein, 1999; Urban, 1998).

4. Balanceo de línea en U considerando riesgos ergonómicos

La asignación de las tareas entre las estaciones de trabajo se alinea respetando las relaciones de precedencia que se puedan dar en la línea de producción. Pero, los tiempos asignados a dos estaciones de trabajo pueden ser iguales. Sin embargo, la carga de trabajo y las condiciones ergonómicas siempre serán diferentes. Esta condición lleva a que los trabajadores realicen actividades de manera recurrente, que los deja expuesto a desordenes musculo esqueléticos. Las líneas de ensamble mal diseñadas, no solo repercute en la productividad, sino también la presencia de enfermedades profesionales de los trabajadores (Baykasoʇlu & Demirkol Akyol, 2014). La consideración de riesgos ergonómicos dentro del balanceo de una línea de ensamble en U, permite la reducción de riesgos musculo esqueléticos de los trabajadores inmersos dentro del procesos productivo; al mismo tiempo, se mejora el rendimiento y la productividad del sistema en función de las estaciones de trabajo y el tiempo de ciclo de la línea de ensamble (Xu et al., 2012). Se hará uso del método OCRA para la cuantificación de riesgos ergonómicos.

A continuación se muestran algunos esquemas en el desarrollo de un balanceo de línea en U de la Figura 1 .c con la información de la Tabla 2 y los diversos indicadores de riesgos ergonómicos. De acuerdo con los resultados (Tabla 6 ) la primera alternativa tiene dos estaciones de trabajo con riesgo ligero, y dos estaciones con riesgo muy ligero de acuerdo con el índice OCRA Check List. Por otra parte la segunda alternativa de balanceo tiene tres estaciones con riesgo ligero, y una estación con riesgo muy ligero con base en el índice OCRA Check List. Estos resultados muestran que las diferentes configuración que se establezcan dentro del balance de línea en U, afecta significativamente el nivel de riesgo que perciben los trabajadores dentro de la línea de ensamble. De la misma manera sucede con otros métodos de valoración ergonómica como el método NIOSH.

Tabla 6 . Alternativas de balanceo de línea en U, Ejemplo (Figura 1 y Tabla 1 )

4.1. Ergo-UALBP

Aplicando el modelo UALBP se sugiere una forma de incorporar los riesgos ergonómicos. El resultado del modelo es abreviado por Ergo-UALBP. El modelo que tome en consideración el nivel de riesgos valorados por medio de los distintos métodos ergonómicos, se da por la inclusión de una restricción ergonómica. En este sentido, completamos las restricciones (8) a (13) de UABLP-1 con la restricción (14), donde F es una función de estimación de riesgo ergonómico con las propiedades en la sección 2.3 y Erg es un coeficiente que establece el nivel máximo aceptable de riesgos ergonómicos. El resultado del modelo es llamado Ergo-UALBP-C

5. Validación de Balanceo de Línea en U Considerando Riesgos Ergonómicos (Ergo-UALBP-C)

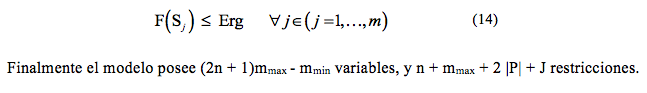
Aplicando el modelo de balanceo de línea en U con el ejemplo base, la información de Tabla 1, y considerando la incorporación de riesgos ergonómicos a través del uso del indicador Check List OCRA, donde se establecen 2 estaciones de trabajo mínimo y 5 estaciones de trabajo como límite máximo de puesto de trabajo. De esta manera se plantea el modelo matemático, adicionado la siguiente restricción como referente de nivel de riesgo ergonómico por actividades repetitivas.

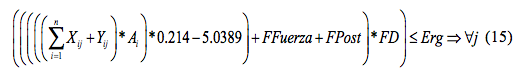
Donde: Ai = corresponde al número de acciones de por tarea i. De esta manera calculamos el factor de Frecuencia (FF) de acuerdo con los estándares establecidos por la metodología Check List OCRA, el cual se adiciona el Factor de Fuerza (FFuerza) y Factor Postura (FP). Además es necesario un Factor de Frecuencia (FD) que para el caso del modelo base será de 1 que corresponde al desarrollo de las actividades en un periodo de 7 a 8 horas laborales. Se ha tomado como nivel aceptable el valor de 9.5, lo que significa para la metodología OCRA un nivel muy ligero.

El problema es resuelto utilizando ILOG CPLEX 12.0 en un computador persona Intel Core I5 de 2.40 GHz con 4 Megas de Memoria. El modelo matemático planteado posee 52 restricciones y 123 variables binarias. Los resultados de la implementación del modelo se evidencian en la Tabla 6 y Figura 4 . Dentro de los resultados, se establecen comparaciones entre modelo de línea en U que toma en consideración los riesgos ergonómicos (Ergo-UALBP-C) y un problema normal en U (UALBP), además de cotejarlo con el modelo tradicional de línea de ensamble (SALBP) y una línea de ensamble en línea con riesgos ergonómicos (Ergo- SALBP-C) como lo planteo Otto et al. (2011).

Las respuestas arrojadas por el modelos Ergo-UALBP-C, arroja un total de 5 estaciones de trabajo, sobre las cuales se balancea los riesgos ergonómicos dentro de las estaciones de trabajo. Los resultados muestran que el nivel de riesgos ergonómicos (Tabla 7 ), son todos “Muy Ligero”, con un valor máximo de 9.4. La media de 9.03 y desviación estándar de 0,44 ponen en evidencia como los riesgos se balancea y distribuyen de una manera muy equitativa entre las estaciones de trabajo. Mientras en un esquema UALBP (Figura 4 .b) el nivel de riesgo se distribuyen con diferentes niveles de riesgo que van desde un nivel óptimo a un nivel medio, con un valor máximo de 16, para 4 estaciones de trabajo. En un escenario Ergo- SALBP-C, el modelo necesito extender el nivel de riesgo ergonómico a 10.4, y de esta manera hallar un respuestas óptima. El modelo permite que el nivel de riesgo se encuentre entre aceptable y muy ligero. En un contexto SALBP se minimiza las estaciones en 4, pero los riesgos van desde un nivel aceptable a un nivel medio, con un valor máximo de riesgo de 16.

Tabla 7 . Resultados de Balanceo de Línea: Ergo-UALBP-c, Ergo-SALBP-c, UALBP y SALBP.

Figura 4 . Esquema de Balanceo de Línea. a) Ergo-UALBP-c; b) UALBP; c) Ergo-SALBP, d) SALBP.

Un esquema de balance de línea en U que toma en consideración los riesgos ergonómicos, aunque no minimiza el número de estaciones de trabajo, es muy bueno en la optimización del bienestar de los trabajadores, debido a que permite balancear el nivel de riesgo ergonómico y reducirlo considerablemente, permitiendo combinaciones de operaciones dentro de la secuencia de ensamble, lo cual no sucede en un modelo de línea de ensamble tradicional. En contraste escenarios de líneas de ensamble tradicionales y en líneas en U, aunque disminuyen el número de estaciones, no balancean la carga de trabajo, la cual pone en riesgo a los trabajadores encargados de las operaciones.

6. Conclusiones

En este trabajo se adaptó un modelo UALBP, con el objetivo de incluir aspectos ergonómicos sobre los trabajadores, como un estrategia para minimizar el desarrollo de trastornos musculo esqueléticos. Se validó un esquema ergonómico, cuando se restringe la línea en U, con el nivel de riesgo admisible sobre las operaciones de ensamble. Este enfoque es fundamentado en la inclusión de riesgos ergonómicos en el balanceo de una línea desarrollada por Otto & Scholl, (2011). La investigación demostró que el problema Ergo-UABLP puede balancear la línea de ensamble y al mismo tiempo disminuir el nivel de riesgo percibido por los trabajadores. Además, futuras aplicaciones necesitan nuevas aplicaciones a distintas instancias con el objetivo de analizar la robustez de este enfoque. Considerar el nivel de riesgos ergonómicos por actividades repetitivas toma una alta relevancia dentro de las líneas de ensamble, debido a que las operaciones cuentan con recursos limitados (tiempo, estaciones) para el desarrollo de productos o bienes. El modelo plateado permite analizar la inclusión de distintas técnicas y metodologías de análisis de puestos de trabajo que consideren factores ergonómicos desde una condición estática del puesto, futuros trabajos deben visionar las jornadas laborales en contexto de competencia, desempeño, descanso, monotonía, y cansancio.

Por otra parte, La inclusión de una restricción ergonómica (Ecuación 14) tiene sus limitaciones, debido a que una respuesta óptima siempre requerirá el máximo de estaciones de trabajo, como se dio en el problema planteado (sección 5), debido a que el modelo siempre buscara distribuir y dar balance a los niveles de riesgos en todas las estaciones de trabajo posible, lo cual es inviable en un sistema productivo donde existen limitantes por costos o distribución de espacios. Otros limitantes se presentan cuando no existe la posibilidad de alternar las tareas entre estaciones por la existencia de niveles de riesgos críticos que hacen inviable la implementación de este tipo de medidas, dada a la dificultad de combinar con otro conjunto de tareas. En estos casos es aconsejable introducir el concepto de rotación laboral como una medida que permita disminuir los periodos de exposición en riesgos que son difíciles de mitigas o combinar con otro conjunto de operaciones.

Además se podrán establecer diferentes estrategias que permitan considerar la inclusión de riesgos ergonómicos dentro de un modelo de balaceo de línea, como lo puede ser incluyendo este tipo de restricciones en la función objetivo, con las variaciones necesarias del caso (disminuir el nivel de riesgo promedio, distribuir la carga o riesgo, minimizar las estaciones afectadas con niveles altos de riesgo). De acuerdo como lo señalado por J. Miltenburg et al. (1994), un problema simple de líneas de ensamble no son muy amplios, y podrían estar compuestos de al menos 30 tareas y 10 estaciones de trabajo, lo cual requiere métodos eficientes y rápidos para hallar respuestas adecuadas muy cercanas al optimo, es por tal motivo que se recomienda el uso de técnicas heurísticas o metaheurísticas de la misma manera como han sido aplicadas en la solución de problemas tradicionales de balanceo de línea.

Referencias 

AASE, G. R., OLSON, J. R., & SCHNIEDERJANS, M. J. (2004). U-shaped assembly line layouts and their impact on labor productivity: An experimental study. European Journal of Operational Research, 156(3), 698–711. http://doi.org/10.1016/S0377-2217(03)00148-6

APTEL, M., AUBLET-CUVELIER, A., & CNOCKAERT, J. C. (2002). Work-related musculoskeletal disorders of the upper limb. Joint Bone Spine, 69(6), 546–555.

BATTAÏA, O., & DOLGUI, A. (2013). A taxonomy of line balancing problems and their solutionapproaches. International Journal of Production Economics, 142(2), 259–277. http://doi.org/10.1016/j.ijpe.2012.10.020

BATTINI, D., DELORME, X., DOLGUI, A., & SGARBOSSA, F. (2015). Assembly line balancing with ergonomics paradigms: two alternative methods. IFAC-PapersOnLine, 48(3), 586–591. http://doi.org/http://dx.doi.org/10.1016/j.ifacol.2015.06.145

BATTINI, D., FACCIO, M., PERSONA, A., & SGARBOSSA, F. (2011). New methodological framework to improve productivity and ergonomics in assembly system design. International Journal of Industrial Ergonomics, 41(1), 30–42. http://doi.org/10.1016/j.ergon.2010.12.001

BAYKASOʇLU, A., & DEMIRKOL AKYOL, Ş. (2014). Ergonomic assembly line balancing . Journal of the Faculty of Engineering and Architecture of Gazi University, 29(4), 785–792. Retrieved from http://www.scopus.com/inward/record.url?eid=2-s2.0-84920196395&partnerID=40&md5=202288de9e979e5807310fa21a7d466c

BERNARD, B. P., & PUTZ-ANDERSON, V. (1997). Musculoskeletal disorders and workplace factors: a critical review of epidemiologic evidence for work-related musculoskeletal disorders of the neck, upper extremity, and low back. US Department of Health and Human Services, Public Health Service, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health Cincinnati, OH, USA.

BOYSEN, N., FLIEDNER, M., & SCHOLL, A. (2007). A classification of assembly line balancing problems. European Journal of Operational Research, 183(2), 674–693. http://doi.org/10.1016/j.ejor.2006.10.010

CARNAHAN, B. J., NORMAN, B. A., & REDFERN, M. S. (2001). Incorporating physical demand criteria into assembly line balancing. Iie Transactions, 33(10), 875–887.

CARNAHAN, B. J., & REDFERN, M. S. (1998). Application of genetic algorithms to the design of lifting tasks. International Journal of Industrial Ergonomics, 21(2), 145–158. http://doi.org/10.1016/S0169-8141(96)00077-7

CHENG, C. H., MILTENBURG, J., & MOTWANI, J. (2000). The effect of straight- and U-shaped lines on quality. Engineering Management, IEEE Transactions on. http://doi.org/10.1109/17.865901

COSTA, A. M., & MIRALLES, C. (2009). Job rotation in assembly lines employing disabled workers. International Journal of Production Economics, 120(2), 625–632. http://doi.org/10.1016/j.ijpe.2009.04.013

DAVID, G. C. (2005). Ergonomic methods for assessing exposure to risk factors for work-related musculoskeletal disorders. Occupational Medicine (Oxford, England), 55(3), 190–199. http://doi.org/10.1093/occmed/kqi082

DEMPSEY, P. G., MCGORRY, R. W., & MAYNARD, W. S. (2005). A survey of tools and methods used by certified professional ergonomists. Applied Ergonomics, 36(4 SPEC. ISS.), 489–503. http://doi.org/10.1016/j.apergo.2005.01.007

EN, N. F. (2007). 1005-5-Safety of machinery–Human physical performance–Part 5. Paris, AFNOR.

FATTAHI, A., & TURKAY, M. (2015). On the MILP model for the U-shaped assembly line balancing problems. European Journal of Operational Research, 242(1), 343–346.

FERGUSON, S. A., MARRAS, W. S., GARY ALLREAD, W., KNAPIK, G. G., & SPLITTSTOESSER, R. E. (2012). Musculoskeletal disorder risk during automotive assembly: Current vs. seated. Applied Ergonomics, 43(4), 671–678. http://doi.org/10.1016/j.apergo.2011.10.001

HALL, R. (1983). Zero Inventories, Dow Jones-Irwin, Homewood, IL, 1983. HallZero Inventories1983.

HWANG, R. K., KATAYAMA, H., & GEN, M. (2008). U-shaped assembly line balancing problem with genetic algorithm. International Journal of Production Research, 46(16), 4637–4649.

ISO 11228-3:2007. (2007). Ergonomics ,Manual handling. Part 3: Handling of low loads at high frequency.

KARHU, O., HÄRKÖNEN, R., SORVALI, P., & VEPSÄLÄINEN, P. (1981). Observing working postures in industry: Examples of OWAS application. Applied Ergonomics, 12(1), 13–7. http://doi.org/10.1016/0003-6870(81)90088-0

KAZMIERCZAK, K., WINKEL, Jø., & WESTGAARD, R. H. (2004). Car disassembly and ergonomics in Sweden: current situation and future perspectives in light of new environmental legislation. International Journal of Production Research, 42(7), 1305–1324. http://doi.org/10.1080/00207540310001624393

KRIENGKORAKOT, N., & PIANTHONG, N. (2007). The U-line Assembly Line Balancing Problem. KKU Engineering Journal, 34(3), 267–274.

MCATAMNEY, L., & NIGEL CORLETT, E. (1993). RULA: a survey method for the investigation of work-related upper limb disorders. Applied Ergonomics, 24(2), 91–99. http://doi.org/10.1016/0003-6870(93)90080-S

MILTENBURG, G. J., & WIJINGAARD, J. (1994). The U-Line Line Balancing Problem. Management Science, 40(10), 1378–1388. Retrieved from http://www.jstor.org/stable/2661631\nchrome://zotero/content/tab.xul

MILTENBURG, J. (2001). U-shaped production lines: A review of theory and practice. International Journal of Production Economics, 70(3), 201–214. http://doi.org/10.1016/S0925-5273(00)00064-5

MILTENBURG, J., & SINNAMON, G. (1995). Revisiting the mixed-model multi-level just-in-time scheduling problem. International Journal of Production Research, 33(7), 2049–2052. http://doi.org/10.1080/00207549508904798

MIRALLES, C., GARCÍA-SABATER, J. P., ANDRÉS, C., & CARDÓS, M. (2008). Branch and bound procedures for solving the Assembly Line Worker Assignment and Balancing Problem: Application to Sheltered Work centres for Disabled. Discrete Applied Mathematics, 156(3), 352–367. http://doi.org/10.1016/j.dam.2005.12.012

MONDELO, P. R., TORADA, E. G., & BOMBARDO, P. B. (2010). Ergonomia I. Fundamentos. Univ. Politèc. de Catalunya.

MONDEN, Y. (1983). Toyota production system: practical approach to production management. Engineering & Management Press.

MONDEN, Y. (1995). Toyota production system. Journal of the Operational Research Society, 4, 3–11. http://doi.org/10.1108/eb054703

OCCHIPINTI, E., & COLOMBINI, D. (2005). The occupational repetitive action (OCRA) methods: OCRA index and OCRA checklist. Handbook of human factors and ergonomics methods. http://doi.org/doi:10.1201/9780203489925.ch15

OHNO, K., & NAKADE, K. (1997). Analysis and optimization of a U-shaped production line. Journal of the Operations Research Society of Japan-Keiei Kagaku, 40(1), 90–104.

OTTO, A. (2014). Minimizing Risks for Health at Assembly Lines. In D. Huisman, I. Louwerse, & A. P. M. Wagelmans (Eds.), Operations Research Proceedings 2013 SE  - 46 (pp. 341–346). Springer International Publishing. http://doi.org/10.1007/978-3-319-07001-8_46

OTTO, A., & SCHOLL, A. (2011). Incorporating ergonomic risks into assembly line balancing. European Journal of Operational Research, 212(2), 277–286. http://doi.org/10.1016/j.ejor.2011.01.056

RAJABALIPOUR CHESHMEHGAZ, H., HARON, H., KAZEMIPOUR, F., & DESA, M. I. (2012). Accumulated risk of body postures in assembly line balancing problem and modeling through a multi-criteria fuzzy-genetic algorithm. Computers and Industrial Engineering, 63(2), 503–512. http://doi.org/10.1016/j.cie.2012.03.017

RODGERS, S. H. (1992). A Functional Job Analysis Technique. Occupational Medicine (Philadelphia, Pa.), 7(4), 679–711. Retrieved from http://www.ncbi.nlm.nih.gov/pubmed/1411855

SCHAUB, K., CARAGNANO, G., BRITZKE, B., & BRUDER, R. (2013). The European assembly worksheet. Theoretical Issues in Ergonomics Science, 14(6), 616–639.

SCHOLL, A., & KLEIN, R. (1999). ULINO: Optimally balancing U-shaped JIT assembly lines. International Journal of Production Research, 37(4), 721–736.

SCHONBERGER RICHARD, J. (1982). Japanese Manufacturing Techniques: Nine Hidden Lessons in Simplicity. New York: Free Press.

SNOOK, S. H., & CIRIELLO, V. M. (1991). The design of manual handling tasks: revised tables of maximum acceptable weights and forces. Ergonomics, 34(9), 1197–213. http://doi.org/10.1080/00140139108964855

STEVEN MOORE, J., & GARG, A. (1995). The strain index: a proposed method to analyze jobs for risk of distal upper extremity disorders. American Industrial Hygiene Association, 56(5), 443–458.

URBAN, T. L. (1998). Note. Optimal Balancing of U-Shaped Assembly Lines. Management Science, 44(5), 738–741. http://doi.org/10.1287/mnsc.44.5.738

VALHONDO, B. (2013). Extended Models for TSALBP with Ergonomic Risk Constraints. In B. Natalia (Ed.), IFAC Proceedings Volumes (IFAC-PapersOnline) (pp. 839–844). http://doi.org/10.3182/20130619-3-RU-3018.00293

WATERS, T. R., PUTZ-ANDERSON, V., GARG,  A, & FINE, L. J. (1993). Revised NIOSH equation for the design and evaluation of manual lifting tasks. Ergonomics, 36(7), 749–776. http://doi.org/10.1080/00140139308967940

WESTGAARD, R. H., & WINKEL, J. (1997). Ergonomic intervention research for improved musculoskeletal health: A critical review. International Journal of Industrial Ergonomics, 20(6), 463–500. http://doi.org/10.1016/S0169-8141(96)00076-5

XU, Z., KO, J., COCHRAN, D. J., & JUNG, M.-C. (2012). Design of assembly lines with the concurrent consideration of productivity and upper extremity musculoskeletal disorders using linear models. Computers & Industrial Engineering, 62(2), 431–441. http://doi.org/10.1016/j.cie.2011.10.008  

1. Doctor Ingeniero Industrial. Grupo de Investigación PRODUCOM. Universidad de la Costa. Cra. 55 # 58-66, Barranquilla- Colombia. jcoronad18@cuc.edu.co
2. Master en Ingenieria. Grupo de Investigación GIPC. Universidad Tecnológica de Bolívar. Parque Tecnológico Carlos Vélez Pombo. Cartagena de Indias-Colombia. hospina@unitecnologica.edu.co