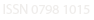
HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 30) Año 2016. Pág. 7

Estrategia Mariposa mediante opciones europeas de compra y venta en escenarios Monte Carlo con volatilidad conducida por un modelo GARCH-M (1,1)

Butterfly Strategy using European call and put options in Monte Carlo scenarios with volatility driven by a GARCH-M (1, 1) Model

Ambrosio ORTIZ-Ramírez 1; Héctor Alonso OLIVARES Aguayo 2; Gabriel Alberto AGUDELO Torres 3; Luis Ceferino FRANCO Arbeláez 4; Luis Eduardo FRANCO Ceballos 5

Recibido: 28/05/16 • Aprobado: 23/06/2016

Contenido

1. Introducción

2. Modelo ARCH-M

3. Modelo GARCH de valuación de opciones financieras

4. Aplicación y análisis de resultados

5. Conclusiones

Bibliografía

1. Introducción

En este artículo se distingue una parte del proceso de toma de decisiones de un individuo que requiere invertir en un activo riesgoso (una opción financiera). Su objetivo es obtener ganancias al destinar parte de su riqueza a la compra de la opción financiera. Sin embargo debe considerar el riesgo al que está expuesto al implementar estrategias para disminuir las pérdidas potenciales que pudiera tener, esto es, generando una cantidad finita de posibles escenarios previos a su decisión de inversión. Las estrategias son generadas al comprar y vender opciones financieras, de acuerdo con la expectativa del inversionista sobre el comportamiento del mercado. Las estrategias de inversión son útiles porque el agente puede protegerse, tanto de los cambios del precio del subyacente y por supuesto de la volatilidad. Es por ello que las estrategias pueden clasificarse en cinco clases: alcistas, bajistas, neutrales, de arbitraje y de volatilidad, como plantea McMillan (2002). Sin embargo el factor más importante para determinar el precio de una opción financiera es la incertidumbre asociada a la dinámica del activo subyacente, usualmente medida por su volatilidad, y cuya fuente son los cambios drásticos en precio y del mercado. La volatilidad es una variable clave que está implícita en la mayoría de los instrumentos financieros y juega un papel central en muchas áreas de finanzas cuantitativas. Por ejemplo, la volatilidad es fundamental en los modelos de valuación de activos y en estrategias de cobertura dinámica, así como en la determinación de los precios de las opciones financieras. De acuerdo con  Cont (2001) una de las características de los rendimientos de las series de tiempo financieras es que su media parece ser constante mientras su varianza cambia con el tiempo. Además los rendimientos muestran clusters de volatilidad: grandes cambios en los rendimientos son seguidos por otros grandes cambios. Tal fenómeno fue estudiado por primera vez en Mandelbrot (1963). Otra característica es que la distribución de los rendimientos tiende a tener colas más gordas en comparación con la distribución normal. Uno de los primeros economistas que trabajó sobre estos fenómenos, también conocidos como hechos estilizados, fue Engle (1982) con el modelo autorregresivo de heterocedasticidad condicional (ARCH). Bollerslev (1986) lo extendió al modelo generalizado (GARCH).

La fórmula de Black y Scholes (1973) y Merton (1973) basada en el supuesto de que el precio del activo subyacente sigue un proceso de difusión lognormal con volatilidad constante, es la referencia usual para calcular precios de opciones financieras sobre un subyacente sin pago de dividendos. No obstante, desde el punto de vista del mercado, este supuesto no se cumple; por ejemplo, las volatilidades implícitas obtenidas con el modelo de Black y Scholes para diferentes plazos y precios de ejercicio no son constantes y tienden a ser en forma de sonrisa. Durante las últimas décadas múltiples trabajos han propuesto extensiones al modelo Black y Scholes para explicar este hecho estilizado. Un enfoque propuesto por Merton (1973) asume que la volatilidad sea una función determinista del tiempo. Otros modelos que tratan con la heteroscedasticidad incluyen, el modelo de elasticidad constante en la varianza (constant-elasticity-of-variance model) de Cox (1975), Christoffersen, Elkamhi, Feunou y Jacobs (2010), Hao y Zhang (2013), entre otros.

Los modelos GARCH han resultado ser herramientas muy efectivas en la resolución de problemas que involucran la volatilidad como variable de interés. La fortaleza más grande de los modelos GARCH es su capacidad para describir las propiedades de la varianza de las series de tiempo de los rendimientos de las variables financieras. Varias extensiones del modelo básico son capaces de describir hechos más atípicos de datos financieros, tales como los diferentes impactos de perturbaciones positivas y negativas en la volatilidad futura (véase Bollerslev, 2008, para una lista, aunque no exhaustiva, sobre los modelos GARCH). Algunos artículos relacionados con la valuación de opciones son, por ejemplo, la caracterización de la medida neutral al riesgo en el caso GARCH para valuar una opción basada en la función de utilidad de un agente representativo planteada por Duan (1995). Heston y Nandi (2000) proporcionan una fórmula cerrada para el precio de la opción con un modelo GARCH  para la volatilidad, aunque implica el cálculo de una integral compleja por métodos numéricos. Angelidis, Benos y Degiannakis (2004) aplican los modelos GARCH al cálculo del Valor en Riesgo (VaR) y muestran que el uso de la distribución t-Student en lugar de una distribución normal  mejora notablemente los pronósticos de VaR.

Este artículo propone la construcción de estrategias mediante la expectativa del inversionista en la volatilidad del activo subyacente; utilizando opciones europeas con el supuesto de que la volatilidad de la opción financiera es conducida por un modelo GARCH-M calibrado con datos históricos y el precio de la opción financiera se obtiene por simulación Monte Carlo. La hipótesis es que dicho modelo es viable cuando el inversionista tiene una expectativa de que el precio del subyacente se mantenga en el corto plazo; es decir, cuando se espera una volatilidad baja en tal componente el inversionista obtiene ganancias. La metodología propuesta se aplica en la valuación de opciones europeas sobre el Índice de Precios y Cotizaciones (IPC) y sobre cuatro de sus componentes (ALFAA, AMXL, BIMBOA y KIMBERA). Después de esta introducción, el desarrollo del presente artículo es como sigue. En la Sección 2 se presenta una breve descripción del modelo ARCH-M, en la Sección 3 se desarrolla la metodología  propuesta, en la Sección 4 se presentan y analizan los resultados obtenidos; y por último,  se concluye en la Sección 5.

2. Modelo ARCH-M

El modelo ARCH de Engle (1982) es extendido en Engle, Lilien y Robins (1987) en el modelo ARCH-M con el supuesto que la media dependa de los movimientos de la varianza condicional. Enders (2009) explica que una clase particular de los modelos ARCH-M se pueden aplicar a series históricas de precios de activos, dado que una característica fundamental de estos mercados es que los inversionistas adversos al riesgo requieren una compensación para retener un activo riesgoso. Puesto que el riesgo de un activo puede ser medido por la varianza del rendimiento, el premio al riesgo puede incrementarse en función de la varianza condicional del rendimiento.

Engle et al (1987) expresan la idea anterior formulando el rendimiento en exceso del activo riesgoso por retener como sigue:

Esta ecuación explica que el exceso de rendimiento para retener el activo debe ser igual al premio al riesgo:

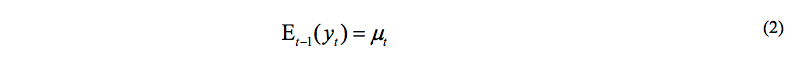
Una generalización del modelo ARCH-M (q) es el modelo GARCH-M (p, q) que considera la varianza condicional como un modelo GARCH dado por:

3. Modelo GARCH de valuación de opciones financieras

El modelo de Black y Scholes, no obstante su renombre, exhibe algunos sesgos sistemáticos. Puesto que la volatilidad del subyacente es uno de los parámetros clave del modelo, el problema radica en si el proceso asumido es consistente con las características de la serie de tiempo del activo subyacente. Dado el hecho de que los modelos GARCH proporcionan una descripción eficiente de la dinámica del precio de un activo, Duan (1995) desarrolla un modelo para valuar opciones europeas que combina las características de los modelos estructurales y estadísticos; es decir, se supone que la volatilidad es conducida por un proceso GARCH calibrado con datos históricos, pero el precio de equilibrio de la opción financiera se basa en argumentos de no arbitraje condicional a la volatilidad del proceso GARCH. Con esos supuestos, el modelo es capaz de reflejar los cambios en la volatilidad condicional del activo subyacente en una forma sencilla.  No obstante, el modelo no tiene una solución en forma cerrada, por lo cual se recurre a la simulación Monte Carlo para obtener el precio de la opción.  A continuación se plantea el modelo.

Suponga que los rendimientos diarios de un activo son independientes e idénticamente distribuidos como una normal:

El rendimiento agregado en días se distribuye también normal con media y varianza escaladas de la siguiente manera:

y el precio futuro del activo es:

Al hacer que el rendimiento pasado entre en la varianza con la magnitud del signo del rendimiento, el efecto de apalancamiento crea una asimetría en la distribución de los rendimientos.  Esta asimetría es importante para capturar el sesgo implícito observado en precios de opciones financieras. Específicamente, se supone que el proceso de rendimientos del subyacente satisface:

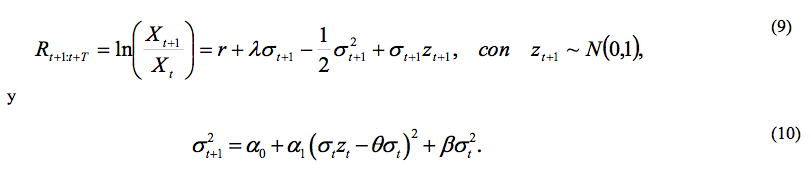
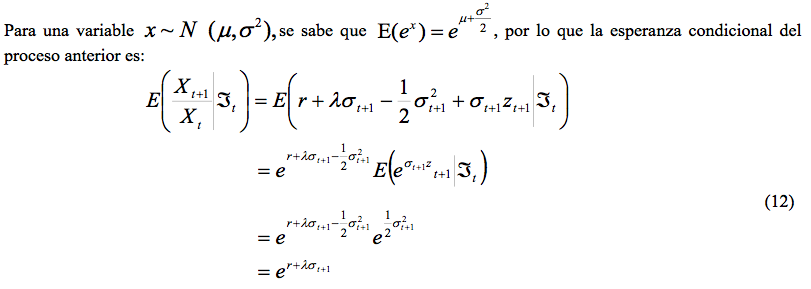
De modo que la tasa esperada de rendimiento en el activo con riesgo es igual a la tasa libre de riesgo y la varianza condicional bajo neutralidad al riesgo es la misma que bajo el proceso original. Considere el proceso siguiente:

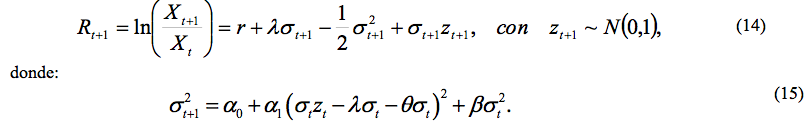
En este caso, se puede comprobar que la esperanza condicional es:

lo cual satisface la primera condición en la ecuación (13). Además, la varianza condicional bajo el proceso neutral al riesgo es:

Donde la última igualdad resulta de la varianza del periodo , que es conocida a final del periodo  en el modelo GARCH-M (1,1). Por lo tanto, se puede concluir que las condiciones para un proceso neutral al riesgo se cumplen.

3.1 Aplicación del modelo por simulación Monte Carlo

Hasta este punto se ha desarrollado un procedimiento para valuar una opción europea bajo neutralidad al riesgo, pero como no se dispone de una fórmula cerrada, se utiliza la simulación Monte Carlo para calcular el precio de la opción financiera como el valor presente del valor intrínseco de una opción de compra:

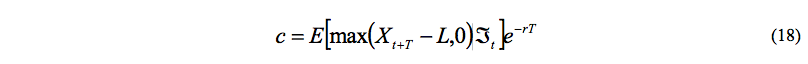
Figura 1: Simulación de los rendimientos t+1 a t+T .

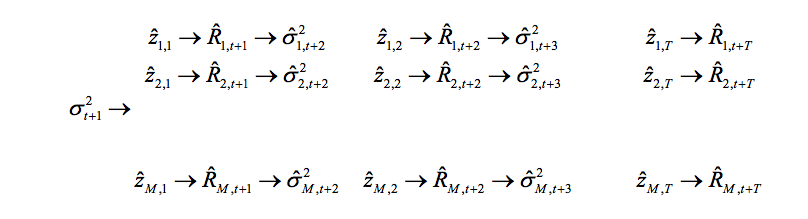
Fuente: elaboración propia.

     Es necesario calcular la esperanza en la ecuación (18) usando el proceso neutral al riesgo. Primero se calcula el rendimiento simulado neutral al riesgo en el periodo  para la trayectoria  de la simulación como:

y la varianza es actualizada por:

Una vez que se han simulado por ejemplo 1,000,000 de trayectorias ( ) cada día hasta la fecha de vencimiento , es posible calcular los precios estimados del activo neutral al riesgo en el vencimiento como:

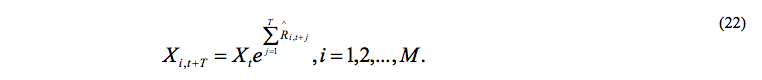
El precio de la opción de compra (call) se calcula como el valor presente del promedio de los pagos futuros estimados:

Para el caso de la opción de venta (put) se tiene:

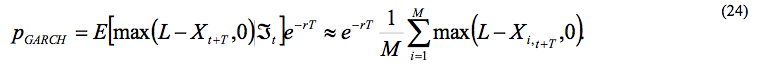
De esta manera se utiliza la simulación para calcular el precio de la opción financiera, que es usado como una estimación del valor esperado en las ecuaciones (23) y (24). En estas condiciones a mayor número de realizaciones del proceso considerado el promedio converge a la esperanza.

4. Aplicación y análisis de resultados

En esta sección se muestra la valuación de opciones europeas de compra y venta sobre el Índice de Precios y Cotizaciones (IPC) y sobre cuatro de sus componentes (ALFAA, AMXL, BIMBOA y KIMBERA) con la metodología propuesta en la sección previa. La muestra comprende del primero de febrero de 2008 hasta el veintidós de marzo de 2013 (1294 observaciones). Para cada serie histórica de los componentes seleccionados se calibró un modelo GARCH-M (1,1) por máxima verosimilitud. Posteriormente se diseñó y se ejecutó un algoritmo para simular trayectorias y precios de opciones para cada componente por simulación Monte Carlo con Matlab, con los cuales se conforma la estrategia Mariposa (baja expectativa de volatilidad). Una Mariposa (Butterfly) consiste en una posición larga de una opción de compra con precio de ejercicio mayor a la opción de venta y entre estos precios de ejercicio se encuentra una posición corta en una opción de compra y en una opción de venta con el mismo precio de ejercicio y vencimiento (Cohen, 2005). Se realizaron 100,000 simulaciones para cada opción de compra y de venta.

Se observan los sectores económicos analizados en esta investigación en la tabla siguiente:

Tabla 1: Distribución de los componentes del IPC.

Fuente: Elaboración propia con datos de Economática.

A continuación con diferentes precios de ejercicio L se muestran los resultados de los valores de las primas de las opciones europeas de compra (call) y de venta (put) para los componentes del IPC y del mismo IPC analizados a plazos de 45 y 90 días.

Tabla 2: Precio de la opción call sobre ALFAA, con precio inicial de 29.83.

Fuente: Elaboración propia con datos obtenidos de Matlab.

Tabla 3: Precio de la opción put sobre ALFAA, con precio inicial de 29.83.

Fuente: Elaboración propia con datos obtenidos de Matlab.

Tabla 4: Precio de la opción call sobre BIMBOA, con precio inicial de 36.6.

Fuente: Elaboración propia con datos obtenidos de Matlab.

Tabla 5: Precio de la opción put sobre BIMBOA, con precio inicial de 36.6.

Fuente: Elaboración propia con datos obtenidos de Matlab.

Tabla 6: Precio de la opción call sobre AMXL, con precio inicial de 12.58.

Fuente: Elaboración propia con datos obtenidos de Matlab.

Tabla 7: Precio de la opción put sobre AMXL, con precio inicial de 12.58.

Fuente: Elaboración propia con datos obtenidos de Matlab.

Tabla 8: Precio de la opción call sobre KIMBERA, con precio inicial de 39.77.

Fuente: Elaboración propia con datos obtenidos de Matlab.

Tabla 9: Precio de la opción put sobre KIMBERA, con precio inicial de 39.77.

Fuente: Elaboración propia con datos obtenidos de Matlab.

Tabla 10: Precio de la opción call sobre IPC, con precio inicial de 42,686.68 puntos base.

Fuente: Elaboración propia con datos obtenidos de Matlab.

Tabla 11: Precio de la opción put sobre IPC, con precio inicial de 42,686.68 puntos base.

Fuente: Elaboración propia con datos obtenidos de Matlab.

A partir de la obtención de los precios de las opciones europeas de compra y venta anteriormente descritos, se construyen 40 estrategias Mariposa las cuales se dividen en 5 zonas como se muestra en la figura siguiente:

Figura 2: Representación por zona de la estrategia Mariposa.

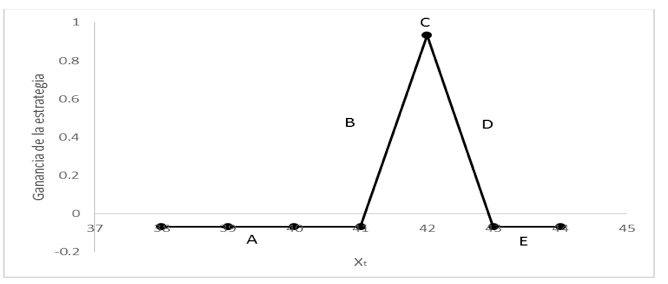
Fuente: Elaboración propia utilizando Excel.

La estrategia se compone por cinco zonas. La zona A y E, representa las máximas pérdidas, la zona c la máxima ganancia y las zonas B y D las ganancias intermedias, por lo cual con la estrategia Mariposa la expectativa del inversionista es de baja volatilidad; es decir, se espera que el valor del activo subyacente no tenga una alta variación para que se pueda obtener ganancias con esta estrategia.

En las siguientes tablas se observan los resultados obtenidos mediante la estrategia Mariposa a plazos de 45 y 90 días.

Tabla 12: Distribución de las 20 estrategias Mariposa con plazo a 45 días.

Fuente: Elaboración propia utilizando Excel.

En la Tabla 12 se observa que en la distribución de los componentes del IPC se obtuvieron once estrategias Mariposa en la zona de máximas pérdidas, cinco en la zona de ganancias intermedias y ninguna en la zona de máximas ganancias. Y en el análisis del principal indicador de acciones del mercado mexicano (IPC) de las cuatro estrategias elaboradas, en dos se obtuvieron ganancias intermedias.

Tabla 13: Distribución de las 20 estrategias Mariposa con plazo a 90 días.

Fuente: Elaboración propia utilizando Excel.

En la Tabla 13 se observa que en la distribución de los componentes del IPC se obtuvieron diez estrategias Mariposa en la zona de máximas pérdidas, seis en la zona de ganancias intermedias y ninguna en la zona de máximas ganancias. Sin embargo, al analizar el principal indicador de acciones del mercado mexicano (IPC) de las cuatro estrategias elaboradas, las cuatro cayeron en zona de máximas pérdidas.

En el análisis realizado se observó que la empresa Kimberly-Clark es la más consistente en zonas de la estrategia Mariposa a los plazos analizados. En el análisis realizado a 45 días se observa que en el IPC y en sus componentes se pudieron obtener ganancias mediante la estrategia empleada, mientras que a 90 días las pérdidas son máximas en el IPC.  Por lo tanto la estrategia Mariposa es una estrategia viable para el IPC a 45 días pero no lo es a 90 días. Lo anterior se observa en las tablas y figuras siguientes:

Tabla 14: Estrategia Mariposa para el componente ALFAA a 45 días.

Fuente: Elaboración propia utilizando Excel.

Figura 3: Gráfica de la estrategia Mariposa para el componente ALFAA a 45 días.

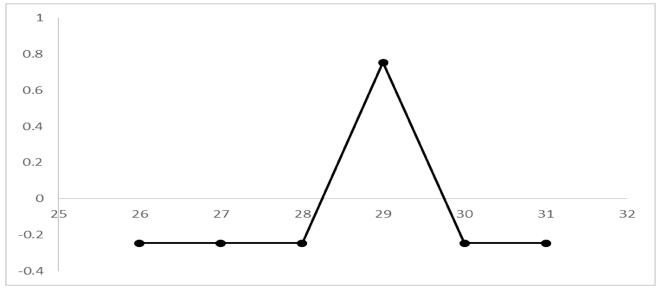
Fuente: Elaboración propia utilizando Excel.

Tabla 15: Estrategia Mariposa para el componente AMXL a 45 días.

Fuente: Elaboración propia utilizando Excel.

Figura 4: Gráfica de la estrategia Mariposa para el componente AMXL a 45 días.

Fuente: Elaboración propia utilizando Excel.

Tabla 16: Estrategia Mariposa para el componente BIMBOA a 45 días.

Fuente: Elaboración propia utilizando Excel.

Figura 5: Gráfica de la estrategia Mariposa para el componente BIMBOA a 45 días.

Fuente: Elaboración propia utilizando Excel.

Tabla 17: Estrategia Mariposa para el componente KIMBERA a 45 días.

Fuente: Elaboración propia utilizando Excel.

Figura 6: Gráfica de la estrategia Mariposa para el componente KIMBERA a 45 días.

Fuente: Elaboración propia utilizando Excel.

Para el mercado mexicano (IPC)  a 45 días la estrategia Mariposa analizadaque representó la mayor ganancia fue la siguiente:

Tabla 18: Estrategia Mariposa para el IPC a 45 días.

Fuente: Elaboración propia utilizando Excel.

Figura 7: Gráfica de la estrategia Mariposa para el IPC a 45 días.

Fuente: Elaboración propia utilizando Excel.

      Los resultados de la estrategia Mariposa a 90 días se muestran a continuación:

Tabla 19: Estrategia Mariposa para el componente ALFAA a 90 días.

Fuente: Elaboración propia utilizando Excel.

Figura 8: Gráfica de la estrategia Mariposa para el componente ALFAA a 90 días.

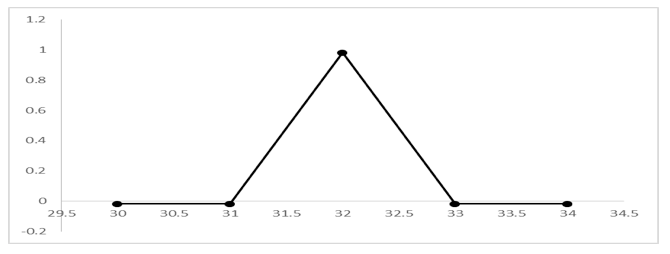
Fuente: Elaboración propia utilizando Excel.

Tabla 20: Estrategia Mariposa para el componente AMXL a 90 días.

Fuente: Elaboración propia utilizando Excel.

Figura 9: Gráfica de la estrategia Mariposa para el componente AMXL a 90 días.

Fuente: Elaboración propia utilizando Excel.

Tabla 21: Estrategia Mariposa para el componente BIMBOA a 90 días.

Fuente: Elaboración propia utilizando Excel.

Figura 10: Gráfica de la estrategia Mariposa para el componente BIMBOA a 90 días.

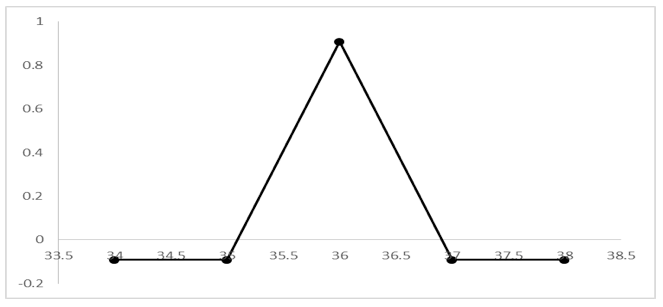
Fuente: Elaboración propia utilizando Excel.

Tabla 22: Estrategia Mariposa para el componente KIMBERA a 90 días.

Fuente: Elaboración propia utilizando Excel.

Figura 11: Gráfica de la estrategia Mariposa para el componente KIMBERA a 90 días.

Fuente: Elaboración propia utilizando Excel.

Para el mercado mexicano (IPC)  a 90 días la estrategia Mariposa analizada que representó la mayor pérdida fue la siguiente:

Tabla 23: Estrategia Mariposa para el IPC a 90 días.

Fuente: Elaboración propia utilizando Excel.

Figura 12: Gráfica de la estrategia Mariposa para el IPC a 90 días.

Fuente: Elaboración propia utilizando Excel.

En la Tabla 23 y en la Figura 12 se observa que al realizar la inversión en el IPC a 90 días se obtiene una pérdida máxima de -136.8440 puntos base. Lo anterior debido a que el valor del IPC cayó drásticamente en el transcurso de los 90 días. Con un valor inicial de 42,686.68 puntos base al 22 de Marzo de 2013 y de 38,036.46 puntos base 90 días después.

5. Conclusiones

En este artículo se ha propuesto una metodología sustentada en conceptos econométricos, financieros y computacionales, de tal manera que proporcione herramientas robustas a un inversionista para la mejora en la toma de decisiones para la conformación de un portafolio de inversión en un contexto de administración de riesgo. En la gran mayoría de temas del análisis de riesgo la medida más utilizada es la volatilidad. Desde un enfoque econométrico la varianza condicional de series de tiempo financieras se utiliza para el cálculo de medidas de riesgo por posiciones en un activo, en la construcción de portafolios y en la valuación de opciones financieras. Para el modelo de Black y Scholes, se supone que los rendimientos son independientes y siguen una distribución normal con varianza constante. Este supuesto no se verifica empíricamente en series de tiempo financieras. Los modelos GARCH son una alternativa que extiende el supuesto de volatilidad constante  del modelo del Black y Scholes.

Se ha presentado la valuación de opciones europeas de compra y venta sobre cuatro componentes del IPC y del mismo IPC, bajo el supuesto de que la volatilidad en los rendimientos del activo subyacente es conducida por un modelo GARCH-M (1,1) calibrado con datos históricos. Puesto que no se cuenta con una fórmula cerrada para el precio de la opción se utilizó un algoritmo de simulación Monte Carlo para obtener el precio de la opción financiera con los supuestos descritos. Con los precios obtenidos se generaron estrategias especulativas de volatilidad para cada componente considerado en el análisis. Una de las ventajas de la simulación Monte Carlo es que permite determinar el valor esperado de las primas de las opciones financieras; es decir, el sustento teórico que hay detrás del método Monte Carlo es la ley de los grandes números, la cual establece que a medida que el número de las simulaciones tiende a infinito, se tendrá una convergencia al valor esperado de la prima de la opción financiera, lo que constituye una metodología robusta al elaborar las estrategias especulativas.

Mediante la estrategia Mariposa se determinó que es posible obtener ganancias en todos los componentes del IPC analizados (ALFAA, AMXL, BIMBOA y KIMBERA) al realizar inversiones con temporalidades de 45 y 90 días. Asimismo esta estrategia también es adecuada en inversiones a 45 días en el IPC, pero no lo fue en inversiones a 90 días, producto de la gran caída que sufrió el principal índice del mercado mexicano. Es decir, la estrategia Mariposa no es adecuada para estimar eventos extremos en el comportamiento de los precios de los activos subyacentes. Se observó que la estrategia Mariposa genera  resultados aceptables al invertir en los componentes del IPC analizados (ALFAA, AMXL, BIMBOA y KIMBERA). Esto resultó factible, debido a que los precios de estos componentes tuvieron una pequeña variación en los diferentes periodos de tiempo de inversión a corto plazo. Por lo tanto el precio se mantuvo estable y al no mostrar cambios significativos la estrategia Mariposa fue viable para poder obtener ganancias en los componentes del IPC.    

Bibliografía

ANGELIDIS, T., A. Benos, y S. Degiannakis (2004). “The use of GARCH models in VaR estimation”, Statistical Methodology, vol. 1, no. 2, pp. 105-128.

BLACK, F. y M. Scholes (1973). “The Pricing of Options and Corporate Liabilities”, The Journal of Political Economy, vol. 81, no. 3, pp. 637-654.

BOLLERSLEV, T. (1986). “Generalized Autoregressive Conditional Heteroskedasticity”, Journal of Econometrics, vol. 31, no. 3, pp. 307-327.

BOLLERSLEV, T. (2008). Glossary to ARCH (GARCH). In T. Bollerslev, J.R. Russell and M. Watson (editores), Volatility and Time Series Econometrics: Essays in Honor of Robert F. Engle. Oxford: Oxford University Press.

COHEN, G. (2005). The bible of options strategies, the definitive guide for practical trading strategies (1a. ed.), Upper Saddle River, New Jersey, USA, Financial Times Prentice Hall.

CONT, R., 2001. “Empirical properties of asset returns: Stylized facts and statistical issues”, Quantitative Finance, vol. 1, pp. 223-236.

COX, J. (1975). “Notes on Option Pricing I: Constant Elasticity of Variance Diffusions”, Working Paper, Stanford University.

CHRISTOFFERSEN, P., R. Elkamhi, B. Feunou, y K. Jacobs (2010). “Option Valuation with Conditional Heteroskedasticity and Non-Normality”, Review of Financial Studies, vol. 23, no. 5, pp. 2139-2183.

DUAN, J. (1995). “The GARCH Option Pricing Model”, Mathematical Finance, vol. 5,   no. 1, pp. 13-32.

ENDERS, W. (2009). Applied Econometrics Time Series, Third edition, John-Wiley & Sons.

ENGLE, R. (1982). “Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflations”, Econometrica, vol. 50, no. 4, pp. 987-1008.

ENGLE, R. F., Lilien, D. M. y Robins, R. P. (1987).  “Estimating Time Varying Risk Premia in the Term Structure: The Arch-M Model”,  Econometrica, vol. 55, no. 2, pp. 391- 407.

HAO, Jinji y Zhang, Jin E. (2013). “GARCH Option Pricing Models, the CBOE VIX, and Variance Risk Premium”, Journal of Financial Econometrics, vol. 11, no. 3, pp. 556-580.

MCMILLAN, Lawrence G. (2002). Options as a Strategic Investment (4a. ed.). Prentice Hall.

MANDELBROT, B. (1963). The variation of certain speculative prices. “The Journal of Business”, vol. 36, no. 4, pp. 394-419.

MERTON, C. R. (1973). Theory of Rational Option Pricing, Bell Journal of Economics and Management Science. vol. 4, no. 1, pp. 141-183.

1. Escuela Superior de Economía, Instituto Politécnico Nacional. Correo electrónico: amortiz@ipn.mx
2. Escuela Superior de Economía, Instituto Politécnico Nacional. Correo electrónico: hectorlivares@hotmail.com
3. Departamento de Finanzas, Instituto Tecnológico Metropolitano – ITM. Correo electrónico: albertoagudelo@itm.edu.co

4. Departamento de Finanzas, Instituto Tecnológico Metropolitano – ITM. Correo electrónico: luisfranco@itm.edu.co

5. Departamento de Finanzas, Instituto Tecnológico Metropolitano – ITM. Correo electrónico: luisefranco@itm.edu.co