 HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN
HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN Espacios. Vol. 37 (Nº 28) Año 2016. Pág. 3
Gabriel Alberto AGUDELO Torres 1; Luis Ceferino FRANCO Arbeláez 2; Luis Eduardo FRANCO Ceballos 3
Recibido: 16/05/16 • Aprobado: 20/06/2016
3. Modelación mediante econometría espacial
4. Suavización Whittaker – Henderson
RESUMEN: En este artículo se propone una metodología para valorar las reservas actuariales de los seguros de vida en una región, considerando las particularidades de sus subregiones y las interacciones entre estas. Taylor (2001) realiza un avance en esa dirección mediante una regresión lineal aportando elementos para determinar cómo en diversas líneas de negocios de seguros, el riesgo varía geográficamente. En este artículo la propuesta de Taylor se complementa con tablas de mortalidad interregionales elaboradas usando econometría espacial. Se realiza una aplicación para el caso Argentino. La metodología presentada en este artículo es relevante ya que constituye una alternativa de valoración para aseguradoras y reaseguradoras que operan en diversos países y cuyas reservas pueden ser afectadas por particularidades e interacciones entre regiones. |
ABSTRACT: The goal of this paper is to suggest a methodology for assessing life insurance actuarial reserves in a region, considering the distinctive features of its sub-regions and their interactions. Taylor (2001) advances towards this direction using a linear regression, and he contributes with useful elements in the determination of how the risk varies geographically in different insurance business lines. This paper complements Taylor’s proposal with inter-regional mortality charts created using spatial econometrics. An application for the case of Argentina is performed. The methodology presented in this article is relevant as it constitutes to assess alternatives for insurance and reinsurance companies operating in different countries and whose reserves may be affected by particularities or interactions between regions. |
En el mundo globalizado actual, la dinámica de las relaciones políticas, económicas y sociales, implica constantemente una transferencia de riesgos, entre sectores, regiones o países. Las aseguradoras y reaseguradoras realizan operaciones alrededor del mundo y de esta manera diversifican sus portafolios de productos. De forma natural, la dinámica de los riesgos está influenciada, entre otros, por efectos espaciales de las variables que determinan su comportamiento.
Desde esta perspectiva, la estimación de unas reservas adecuadas para cubrir un riesgo específico, debería tener en cuenta los potenciales efectos espaciales. Taylor (2001) realiza un avance en esa dirección mediante una regresión lineal; su estudio aporta elementos para determinar cómo en diversas líneas de negocios de seguros, el riesgo varía geográficamente.
Los efectos espaciales de dependencia y heterogeneidad, son propios de los datos geográficamente distribuidos (Chasco, 2003), y si una serie presenta atributos de dependencia espacial, esto conlleva también a la existencia de problemas de heterocedasticidad, aunque la inversa no es cierta (Mur, 1999). En este artículo se agrega un modelo espacial al problema inicial planteado por Taylor (2001) para el cálculo y simulación de las reservas de los seguros, y se explica por qué la regresión lineal, planteada por Taylor para abordar el problema, puede ser complementada de forma integral con un modelo espacial. Para ilustrar el enfoque propuesto se realiza una aplicación para el caso argentino.
El presente artículo está organizado cómo sigue: en la Sección 2 se presentan los fundamentos de la dependencia espacial; en la Sección 3 se presenta teóricamente el modelo y estimación de sus parámetros; posteriormente, en la Sección 4, se presenta la graduación de probabilidades de muerte mediante el método Whittaker-Henderson. Luego, en la Sección 5, se presenta la aplicación para el caso argentino; y, por último, en la Sección 6 se exponen las conclusiones.
De acuerdo con las particularidades inherentes a cada región de un espacio geográfico determinado, es de esperarse que la variable probabilidad de muerte en menos de un año para una persona de edad x presente dependencia espacial consigo misma, excepto en edades muy avanzadas, pues estas últimas dependerán del deterioro normal de la salud y no necesariamente de condiciones externas.
En este contexto la econometría espacial llena un vacío existente en la econometría tradicional. La estimación de parámetros se hace inmanejable en un modelo lineal general cuando se incluyen efectos espaciales en cada una de las ecuaciones del modelo. LeSage (2009) ilustra esta situación mediante un ejemplo con tres regiones:
![]()
![]()
![]()
![]()
![]()
![]()
Donde:
![]() : Datos muestrales de la variable endógena en cada una de las regiones (
: Datos muestrales de la variable endógena en cada una de las regiones (![]() ).
).
![]() : Coeficiente correspondiente a la variable endógena en la región
: Coeficiente correspondiente a la variable endógena en la región ![]() para ayudar a explicar la variabilidad en la misma variable en la región
para ayudar a explicar la variabilidad en la misma variable en la región ![]() .
.
![]() : Matriz de variables exógenas de dimensión (
: Matriz de variables exógenas de dimensión (![]() ) que ayuda a explicar la variabilidad en la variable endógena en la región
) que ayuda a explicar la variabilidad en la variable endógena en la región ![]() .
.
![]() : Vector de dimensión (
: Vector de dimensión (![]() ) de parámetros de las variables exógenas que ayudan a explicar la variabilidad en
) de parámetros de las variables exógenas que ayudan a explicar la variabilidad en ![]() , con
, con ![]()
![]() : Vector de perturbaciones aleatorias, ruido blanco, para la ecuación que trata de explicar la variabilidad en
: Vector de perturbaciones aleatorias, ruido blanco, para la ecuación que trata de explicar la variabilidad en ![]() , con
, con ![]()
Se observa que contar con tres observaciones implica estimar seis parámetros, sin tener en cuenta el vector de parámetros ![]() correspondiente a las variables exógenas. Si
correspondiente a las variables exógenas. Si ![]() es el número de observaciones, potencialmente se tendrían que estimar
es el número de observaciones, potencialmente se tendrían que estimar ![]() de estos parámetros.
de estos parámetros.
La solución para el problema de sobreparametrización la propone Ord (1975) al sugerir el proceso espacial autorregresivo:
![]() , donde
, donde ![]() ,
, ![]()
El término ![]() es llamado retardo espacial y representa una combinación lineal de valores de la variable
es llamado retardo espacial y representa una combinación lineal de valores de la variable ![]() en regiones vecinas a la región
en regiones vecinas a la región ![]() .
.
Para desarrollar esta especificación, Ord utilizó la primera ley de la geografía formulada por Tobler (1979), la cual indica que “todo tiene que ver con todo, pero las cosas cercanas están más relacionadas entre sí que las cosas lejanas”. Ord materializó este principio incluyendo en sus modelos econométricos una “matriz de retardos espaciales” o “matriz de contigüidades”![]() , cuyos elementos corresponden a unos (1) si las regiones correspondientes a la fila y a la columnas son vecinas y a ceros (0) en caso contrario.
, cuyos elementos corresponden a unos (1) si las regiones correspondientes a la fila y a la columnas son vecinas y a ceros (0) en caso contrario.
El proceso espacial autorregresivo en forma matricial es entonces:
![]()
![]()
El efecto del operador de retardo sobre una serie espacial es la agregación de las observaciones asociadas a las regiones vecinas. Un ejemplo ilustrativo sobre la construcción de la matriz W y su efecto sobre la vector de observaciones Y puede extraerse de una unidad geográfica con 9 regiones dispuestas tal como se muestra en la Figura 1, donde la vecindad entre ellas se define como la existencia de una frontera común mayor a un punto. El mapa de la unidad geográfica y vector WY serán entonces:
Figura 1: Unidad geográfica compuesta por 9 regiones.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |

Como se observa, el operador de retardo espacial desplaza y agrega las masas de las regiones contiguas a la región analizada.
Este resultado crea un problema de interpretación con la dimensión de la variable resultado. Si se desea preservar la dimensión, basta con imponer la condición de que la suma de los elementos de cada fila sea 1. Se puede entonces tomar cada fila de W y dividir cada componente entre la suma de todas las componentes de la fila respectiva; este proceso da lugar a la “matriz de contactos estandarizada” y supone, no la agregación de masas en el espacio, sino hallar el promedio de éstas.

A partir del proceso espacial autorregresivo que, como se demuestra en Agudelo (2010), produce un estimador de ![]() sesgado e inconsistente, se derivan otros modelos con estimadores insesgados, eficientes, consistentes y suficientes.
sesgado e inconsistente, se derivan otros modelos con estimadores insesgados, eficientes, consistentes y suficientes.
Uno de esos modelos es el llamado Modelo Mixto Autorregresivo de Regresión Espacial, cuya forma funcional es:
![]()
![]()
Este modelo, permite explicar la variabilidad en ![]() a partir de los datos de la misma variable en las regiones vecinas y de otro conjunto de variables exógenas incluidas en la matriz
a partir de los datos de la misma variable en las regiones vecinas y de otro conjunto de variables exógenas incluidas en la matriz ![]() .
.
3.1. Especificación del modelo
Utilizando el modelo mixto autorregresivo de regresión espacial es posible hallar un pronóstico para el vector ![]() , cuyas componentes indican la probabilidad que tiene una persona de edad
, cuyas componentes indican la probabilidad que tiene una persona de edad ![]() de no llegar vivo a la edad
de no llegar vivo a la edad ![]() en la región correspondiente a cada fila. Esto teniendo en cuenta la dependencia espacial existente en las tasas de mortalidad y la relación que existe naturalmente entre la probabilidad de muerte a cierta edad y la probabilidad de muerte a la edad anterior o la edad siguiente; para este modelo se definió la utilización de la edad siguiente pues la aparente dificultad que se presentaría al tratar de modelar la última edad del modelo, se resuelve al asumir que nadie puede sobrevivir a esa edad, es decir que es la edad límite para esa población. Por lo tanto, se asume que
en la región correspondiente a cada fila. Esto teniendo en cuenta la dependencia espacial existente en las tasas de mortalidad y la relación que existe naturalmente entre la probabilidad de muerte a cierta edad y la probabilidad de muerte a la edad anterior o la edad siguiente; para este modelo se definió la utilización de la edad siguiente pues la aparente dificultad que se presentaría al tratar de modelar la última edad del modelo, se resuelve al asumir que nadie puede sobrevivir a esa edad, es decir que es la edad límite para esa población. Por lo tanto, se asume que ![]() , siendo
, siendo ![]() la edad límite del modelo. Asumir un valor para
la edad límite del modelo. Asumir un valor para ![]() sería imposible por la variabilidad existente en las tasas de defunción de recién nacidos.
sería imposible por la variabilidad existente en las tasas de defunción de recién nacidos.
Se considera además, la posible existencia de otro conjunto de variables exógenas que complemente el modelo inicial. La especificación del modelo incluye entonces una matriz de variables exógenas![]() que permite incluir variables explicativas de la variabilidad interregional de la probabilidad de defunción a una edad x.
que permite incluir variables explicativas de la variabilidad interregional de la probabilidad de defunción a una edad x.
![]() , con
, con ![]() y
y ![]()
Donde:
![]() : Vector de
: Vector de ![]() filas (correspondiente al número de regiones) por 1 columna. Indica la probabilidad que tiene una persona de edad
filas (correspondiente al número de regiones) por 1 columna. Indica la probabilidad que tiene una persona de edad ![]() de no llegar vivo a la edad
de no llegar vivo a la edad ![]() en la región correspondiente a la fila. Sus componentes serán denotadas como
en la región correspondiente a la fila. Sus componentes serán denotadas como ![]() con
con ![]() , tal como se muestra en la Figura 2.
, tal como se muestra en la Figura 2.
Figura 2: Probabilidad en la región ![]() de fallecer entre las edades
de fallecer entre las edades ![]() y
y ![]() .
.
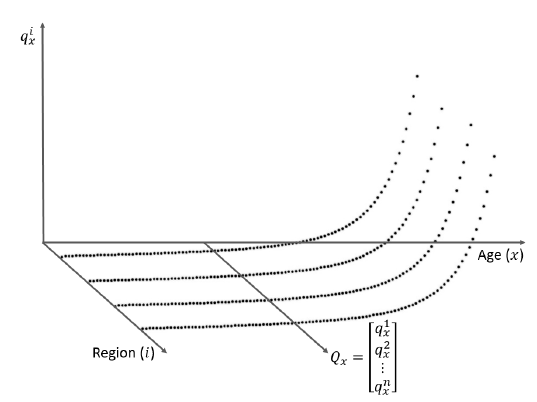
Fuente: elaboración propia
W: Matriz de contigüidades de dimensión ![]() .
.
![]() : Coeficiente autorregresivo espacial (escalar), que recoge la intensidad de las interdependencias entre las observaciones muestrales.
: Coeficiente autorregresivo espacial (escalar), que recoge la intensidad de las interdependencias entre las observaciones muestrales.
![]() : Matriz de contigüidades de orden 1, estandarizada y de dimensión (
: Matriz de contigüidades de orden 1, estandarizada y de dimensión (![]() ).
).
![]() : Vector de
: Vector de ![]() filas (correspondiente al número de regiones) por 1 columna. Indica la probabilidad que tiene una persona de edad
filas (correspondiente al número de regiones) por 1 columna. Indica la probabilidad que tiene una persona de edad ![]() de no llegar vivo a la edad
de no llegar vivo a la edad ![]() en la región correspondiente a la fila.
en la región correspondiente a la fila.
![]() : Matriz de dimensión (
: Matriz de dimensión (![]() ) de variables exógenas que ayudan a explicar la variabilidad en la variable
) de variables exógenas que ayudan a explicar la variabilidad en la variable ![]() .
.
![]() : Vector de parámetros de dimensión (
: Vector de parámetros de dimensión (![]() ), que incluye un parámetro
), que incluye un parámetro ![]() correspondiente al término constante del modelo.
correspondiente al término constante del modelo.
![]() : Término de perturbación aleatoria de dimensión (
: Término de perturbación aleatoria de dimensión (![]() ).
).
La variable ![]() no se rezaga espacialmente porque induciría redundancia en las variables explicativas al tener también dependencia espacial.
no se rezaga espacialmente porque induciría redundancia en las variables explicativas al tener también dependencia espacial.
3.2. Estimación de parámetros
Un estimador insesgado, eficiente, consistente y suficiente del parámetro ![]() se puede obtener mediante el método de máxima verosimilitud o el de mínimos cuadrados ordinarios, convirtiendo el modelo espacial en un modelo lineal general mediante la siguiente sustitución:
se puede obtener mediante el método de máxima verosimilitud o el de mínimos cuadrados ordinarios, convirtiendo el modelo espacial en un modelo lineal general mediante la siguiente sustitución:
![]()
El modelo mixto autorregresivo de regresión espacial se convierte entonces en uno lineal general de la siguiente forma:
![]()
![]()
![]()
![]()
Por lo tanto el estimador de ![]() será:
será:
![]()
![]()
En cuanto al estimador del parámetro ![]() , como
, como ![]() entonces su función de densidad de probabilidad es:
entonces su función de densidad de probabilidad es:
![]()
Donde ![]() y
y ![]() es el tamaño de la muestra.
es el tamaño de la muestra.
Se sabe que la función de densidad de probabilidad de ![]() es
es ![]() , por lo tanto:
, por lo tanto:
![]()
Y la función de log-verosimilitud es:
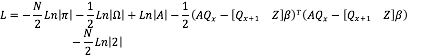
El problema de optimización a resolver es ![]() , por lo que al derivar
, por lo que al derivar ![]() con respecto a
con respecto a ![]() e igualar a cero se obtiene una expresión que se verifica al encontrar el estimador de
e igualar a cero se obtiene una expresión que se verifica al encontrar el estimador de ![]() adecuado.
adecuado.
![]()
Por lo tanto,
![]()
Una vez estimados los parámetros, el modelo tendrá la siguiente forma funcional:
![]()
Trasponiendo el vector ![]() se obtiene:
se obtiene:
![]()
A partir del resultado anterior es posible construir una matriz ![]() conformada por los vectores estimados
conformada por los vectores estimados ![]() para
para ![]() ; donde
; donde ![]() es la edad a la que ninguna persona puede sobrevivir.
es la edad a la que ninguna persona puede sobrevivir.
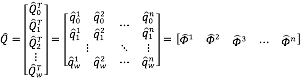
Para obtener tasas de mortalidad consistentes con la teoría, es preciso utilizar algún tipo de método para suavizar cada serie ![]() con
con ![]() . El método que se considera en este artículo es el de Whittaker-Henderson, el cual es frecuentemente utilizado en la práctica actuarial para la construcción de tablas de vida (Nocon y Scott, 2010). A partir de este método se obtienen los vectores suavizados
. El método que se considera en este artículo es el de Whittaker-Henderson, el cual es frecuentemente utilizado en la práctica actuarial para la construcción de tablas de vida (Nocon y Scott, 2010). A partir de este método se obtienen los vectores suavizados ![]()
La graduación de probabilidades de muerte mediante el método Whittaker-Henderson consiste en encontrar el valor de ![]() apropiado tal que se minimice la función
apropiado tal que se minimice la función ![]() , donde
, donde ![]() y
y ![]() son medidas de falta de falta de ajuste y de suavidad, respectivamente. El parámetro k permite realizar una graduación enfocada hacia un mayor ajuste o hacia una mayor suavidad.
son medidas de falta de falta de ajuste y de suavidad, respectivamente. El parámetro k permite realizar una graduación enfocada hacia un mayor ajuste o hacia una mayor suavidad.
Sea ![]() un vector de dimensión (
un vector de dimensión (![]() ) de tasas de mortalidad graduadas mediante el procedimiento Whittaker-Henderson,
) de tasas de mortalidad graduadas mediante el procedimiento Whittaker-Henderson, ![]() es una matriz diagonal de dimensión (
es una matriz diagonal de dimensión (![]() ) cuyos elementos de la diagonal principal corresponden a las ponderaciones asignadas previamente a cada edad o grupo de edades. La matriz
) cuyos elementos de la diagonal principal corresponden a las ponderaciones asignadas previamente a cada edad o grupo de edades. La matriz ![]() corresponde a una matriz cuadrada de dimensión (
corresponde a una matriz cuadrada de dimensión (![]() ) tal que
) tal que ![]() , donde
, donde ![]() es el vector de m diferencias de
es el vector de m diferencias de ![]() .
.
![]()
Donde,
![]()
![]()
Derivando ![]() con respecto a
con respecto a ![]() e igualando a cero, se obtiene:
e igualando a cero, se obtiene:
![]()
El método de validación cruzada generalizada (GCV), fue introducido por Craven y Wahba (1979) y posteriormente fue adaptado por Brooks et al. (1988) para complementar la graduación Whittaker-Henderson. De acuerdo a este método, el parámetro ![]() seleccionado para cada región
seleccionado para cada región ![]() debe minimizar la siguiente expresión:
debe minimizar la siguiente expresión:
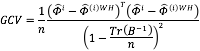
Donde ![]() y
y ![]() corresponde a la traza de la matriz
corresponde a la traza de la matriz ![]() .
.
Las probabilidades estimadas y suavizadas serán entonces:
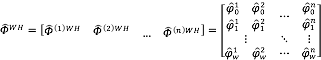
Para ilustrar el procedimiento descrito, se utilizaron tablas de mortalidad correspondientes a provincias de la República Argentina, tal como se muestra en la Figura 3, puesto que dicho país se caracteriza por llevar estadísticas espaciales detalladas de este tipo de variables. Estos datos fueron introducidos en el software GeoDa proveído por el GeoDa Center for Geospatial Analysis and Computation de la Arizona State University.
Figura 3: Unidad espacial de la República Argentina con cada una de sus provincias (regiones).
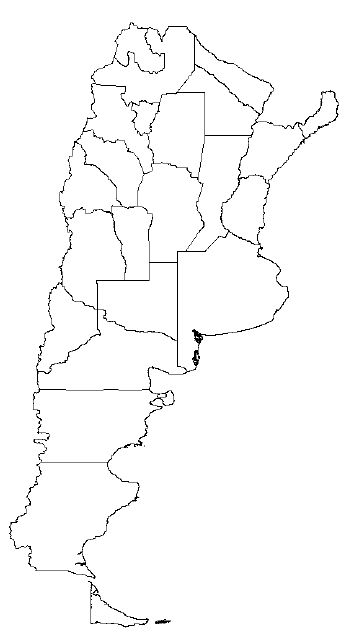
Fuente: elaboración propia.
A partir de la primera ley de Tobler es razonable establecer la hipótesis relacionada con la existencia de dependencia espacial en la probabilidad de muerte antes mencionada. Para verificar o rechazar dicha hipótesis se utilizó el test de Moran para matrices estandarizadas.
![]() No existe dependencia espacial
No existe dependencia espacial ![]()
![]() Existe dependencia espacial
Existe dependencia espacial ![]()
El estadístico de prueba es ![]() y su valor esperado y varianza es:
y su valor esperado y varianza es:
![]()
![]()
Donde:
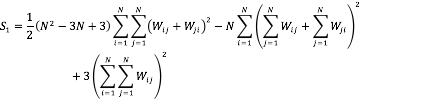
![]()
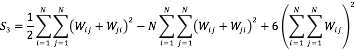
Los resultados de este test son concluyentes con un nivel de significancia de ![]() para todos los grupos de edades utilizados, excepto para la edad
para todos los grupos de edades utilizados, excepto para la edad ![]() y para las edades avanzadas de adultos mayores (
y para las edades avanzadas de adultos mayores (![]() y
y![]() ), como se muestra en la Tabla 1.
), como se muestra en la Tabla 1.
Tabla 1
Pseudo valor – p de la prueba de dependencia espacial para cada edad
Edad |
Pseudo valor-p |
0 |
0.003 |
5 |
0.024 |
10 |
0.001 |
15 |
0.443 |
20 |
0.052 |
25 |
0.041 |
30 |
0.001 |
35 |
0.001 |
40 |
0.002 |
45 |
0.005 |
50 |
0.001 |
55 |
0.001 |
60 |
0.001 |
65 |
0.003 |
70 |
0.030 |
75 |
0.049 |
80 |
0.207 |
85 |
0.225 |
90 |
0.111 |
95 |
0.047 |
Fuente: elaboración propia.
Para efectos prácticos se modelaron todas las edades mediante la técnica expuesta en este artículo, con ![]() como única variable exógena, obteniendo los coeficientes que se muestran en la Tabla 2 y que describen el equilibrio existente entre la probabilidad de fallecer a cierta edad, la probabilidad de fallecer a la misma edad en las regiones vecinas y la probabilidad de fallecer a la edad siguiente. Estimar los parámetros del modelo para edad 95 no es posible, ya que la matriz
como única variable exógena, obteniendo los coeficientes que se muestran en la Tabla 2 y que describen el equilibrio existente entre la probabilidad de fallecer a cierta edad, la probabilidad de fallecer a la misma edad en las regiones vecinas y la probabilidad de fallecer a la edad siguiente. Estimar los parámetros del modelo para edad 95 no es posible, ya que la matriz ![]() es singular.
es singular.
Tabla 2
Coeficientes estimados para el modelo correspondiente a cada edad
|
|
|
|
0 |
0,5163901 |
0,002734458 |
2,663108 |
5 |
-0,1303142 |
0,000801236 |
0,386809 |
10 |
-0,03341898 |
0,000643267 |
0,2631198 |
15 |
0,00706793 |
0,000755391 |
0,5813413 |
20 |
0,1238288 |
0,000198748 |
0,7722609 |
25 |
-0,14511 |
0,000785998 |
0,9420633 |
30 |
0,029756 |
0,000821110 |
0,6665455 |
35 |
-0,09242447 |
0,000577388 |
0,6817012 |
40 |
0,178593 |
-0,000054253 |
0,5227762 |
45 |
0,08305462 |
-0,002790272 |
0,6736886 |
50 |
0,0738117 |
-0,000540754 |
0,6037558 |
55 |
0,02078174 |
0,005737977 |
0,5693396 |
60 |
0,08897329 |
0,008463159 |
0,5329988 |
65 |
0,07737611 |
-0,014813430 |
0,7225336 |
70 |
0,03512513 |
-0,025414990 |
0,7503735 |
75 |
-0,00143098 |
0,006983994 |
0,6264926 |
80 |
-0,00795226 |
0,001226453 |
0,7297006 |
85 |
-0,0142826 |
-0,003639798 |
0,8008919 |
90 |
-0,01167305 |
-0,130147000 |
1,004321 |
Fuente: elaboración propia.
A partir de las ecuaciones normales del modelo, es posible simular el efecto que un cambio en alguna de las variables exógenas tendría en la probabilidad de fallecer a una edad x en una región determinada. Estas probabilidades estimadas deben ser suavizadas para la construcción de tablas de mortalidad regionales que incorporen dicho cambio.
Para el caso argentino se simularon las probabilidades sin incluir cambios en las variables exógenas y se suavizaron mediante el método Whittaker-Henderson con estimación del parámetro ![]() mediante validación cruzada generalizada.
mediante validación cruzada generalizada.
Tabla 3
Probabilidades estimadas de fallecer entre las edades ![]() y
y ![]() para la región
para la región ![]() (
(![]() ).
).
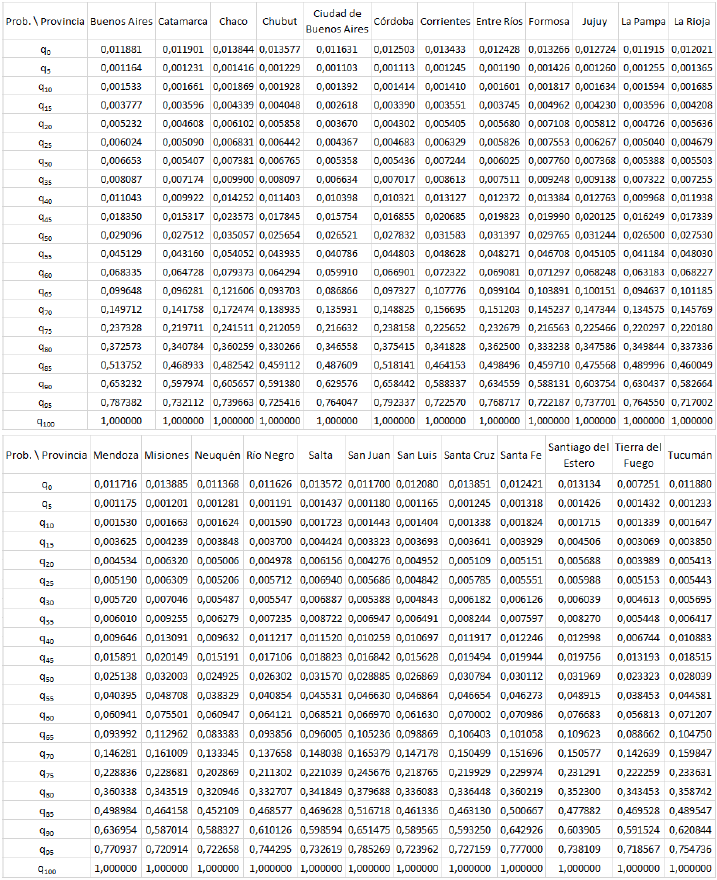
Fuente: elaboración propia.
Tabla 4
Probabilidades (suavizadas) estimadas de fallecer entre las edades ![]() y
y ![]() para la región
para la región ![]() (
(![]() ).
).
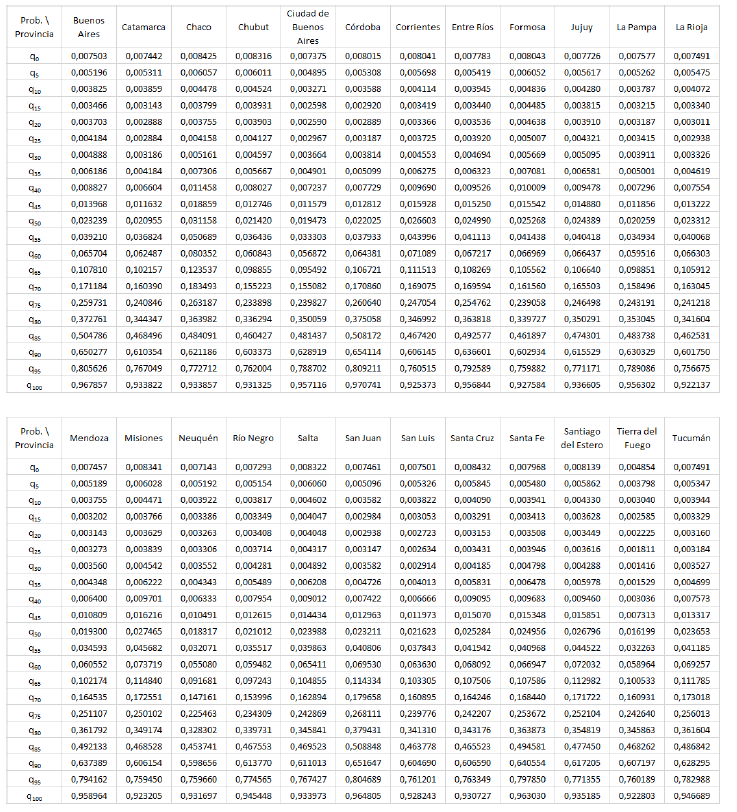
Fuente: elaboración propia.
De acuerdo con las características particulares de las diferentes regiones que conforman un espacio geográfico, es natural que la variable probabilidad de muerte en menos de un año para una persona de edad ![]() presente el fenómeno llamado dependencia espacial. En este sentido, la econometría espacial tiene un papel fundamental en el análisis para la constitución de reservas actuariales adecuadas.
presente el fenómeno llamado dependencia espacial. En este sentido, la econometría espacial tiene un papel fundamental en el análisis para la constitución de reservas actuariales adecuadas.
A través de la econometría espacial es posible elaborar tablas de mortalidad que reflejen las relaciones espaciales interregionales, hallando un pronóstico para el vector ![]() mediante el Modelo Mixto Autorregresivo de Regresión Espacial aplicado en este artículo. El vector
mediante el Modelo Mixto Autorregresivo de Regresión Espacial aplicado en este artículo. El vector ![]() se compone de las probabilidades de fallecer entre las edades x y x+1 en cada una de las regiones del espacio geográfico. Dentro de las variables exógenas del modelo deberán estar incluidos los vectores
se compone de las probabilidades de fallecer entre las edades x y x+1 en cada una de las regiones del espacio geográfico. Dentro de las variables exógenas del modelo deberán estar incluidos los vectores ![]() , que recoge las interacciones espaciales interregionales, y
, que recoge las interacciones espaciales interregionales, y ![]() , que conserva el supuesto básico referente a la mayor probabilidad de muerte a medida que una persona aumenta los años vividos.
, que conserva el supuesto básico referente a la mayor probabilidad de muerte a medida que una persona aumenta los años vividos.
Para obtener estimadores insesgados, eficientes, consistentes y suficientes de los parámetros que relacionan ![]() con las variables exógenas del modelo, se pueden utilizar el método de máxima verosimilitud o el de mínimos cuadrados ordinarios, los cuales son comúnmente utilizados en econometría. Posteriormente, las tasas estimadas deben ser suavizadas mediante alguna técnica de graduación, entre las cuales está el método Whittaker – Henderson, utilizado en este artículo.
con las variables exógenas del modelo, se pueden utilizar el método de máxima verosimilitud o el de mínimos cuadrados ordinarios, los cuales son comúnmente utilizados en econometría. Posteriormente, las tasas estimadas deben ser suavizadas mediante alguna técnica de graduación, entre las cuales está el método Whittaker – Henderson, utilizado en este artículo.
AGUDELO, G. A. (2010) Dependencia Espacial: Detección, Validación y Modelación, Master’s theses, Universidad EAFIT. Medellín, Colombia.
BROOKS, R. J., Stone, M., Chan, F. Y. and Chan, L.K. (1988). Cross-validatory Graduation. Insurance: Mathematics and Economics 7, 59 – 66.
CHASCO, C. (2003). Econometría Espacial Aplicada A La Predicción-Extrapolación De Datos Microterritoriales. Comunidad de Madrid (pp 1–6). Madrid: Consejería de Economía e Innovación Tecnológica.
CRAVEN, P. and Wahba, G. (1979). Smoothing Noisy Data with Spline Functions. Numerical Mathematics 31, 377 – 403.
LESAGE, James and Pace, Robert K. (2009). Introduction to Spatial Econometrics. CRC Press Inc., 354.
MUR, J. (1999). Heterocedasticidad y Autocorrelación espacial: una propuesta de identificación de series espaciales. In Estadística Española. Vol. 41, Núm. 144 (pp 79 – 104). Madrid: Instituto Nacional de Estadística.
NOCON, Alicja S. and Scott, William F. (2010). An Extension of the Whittaker-Henderson method of graduation.
ORD, J.K. (1975). Estimation Methods for Models of Spatial Interaction. Journal of the American Statistical Association, 70, 120-126.
TAYLOR, G. (2001). Geographic Premium Rating by Whittaker Spatial Smoothing, Astin Bulletin, Vol. 31, No. 1; pp. 147-160.
TOBLER, W. (1979). Cellular Geography. Philosophy in Geography, ed. S. Gale y G. Olsson, Dordrecht: Reidel, 379-386.
1. Ingeniero Financiero. Magíster en Matemáticas Aplicadas. Docente Investigador Instituto Tecnológico Metropolitano - ITM. Medellín, Colombia. albertoagudelo@itm.edu.co
2. Matemático. Magíster en Matemáticas Aplicadas. Docente Investigador Instituto Tecnológico Metropolitano - ITM. Medellín, Colombia. luisfranco@itm.edu.co
3. Ingeniero Financiero. Magíster en Finanzas. Docente Investigador Instituto Tecnológico Metropolitano - ITM. Medellín, Colombia. luisefranco@itm.edu.co