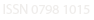
HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 37 (Nº 26) Año 2016. Pág. 5

Otimização Multiobjetivo em uma Linha de Produção de Placas Eletrônicas de uma Pequena Empresa

Multiobjective Optimization in a Production Line of Electronic Boards in a Small Company

Eduardo Ferreira DASSAN 1, Dayane SANTOS 2, Adriano Maniçoba da SILVA 3, Luiz Teruo KAWAMOTO Júnior 4, Enio Fernandes RODRIGUES 5

Recibido: 02/05/16 • Aprobado: 12/05/2016

Conteúdo

1. Introdução

2. Revisão da literatura

3. Metodologia

4. Análise dos resultados

5. Discussão dos resultados

6. Considerações finais

Referências bibliográficas

1. Introdução

A maximização dos lucros é de suma importância para as empresas se manterem estáveis e competitivas no mercado em que atuam. Deste modo, a melhoria dos processos na gestão da produção é fator preponderante para que isto aconteça. Existem diversas ferramentas desenvolvidas no âmbito da Pesquisa Operacional que auxiliam as empresas na melhoria de seus processos produtivos, na determinação da capacidade produtiva, e na melhor utilização dos recursos disponíveis, por meio da utilização de técnicas de modelagem matemática como a Programação Linear.

Maximizar a margem de contribuição para aumentar a competitividade, pode envolver negligenciar outros indicadores importantes tal como a utilização da capacidade. Para utilizar de maneira eficiente os recursos disponíveis, de modo a buscar a melhoria em mais de um indicador, a otimização multiobjetivo pode ser útil a este fim. Desta forma, o presente estudo aborda a aplicação de um modelo matemático para a otimização multiobjetivo numa pequena empresa, que buscou tanto a maximização da utilização da capacidade produtiva de sua linha de montagem de placas eletrônicas e a maximização da margem de contribuição. 

Para a elaboração deste estudo, buscou-se revisar a literatura da Programação Linear e a Otimização Multiobjetivo, ambas aplicadas na resolução do modelo matemático proposto, sendo que o modelo foi realizado no Software Microsoft Excel com o suplemento Solver. A relevância deste estudo justifica-se pela necessidade da empresa otimizar a utilização da capacidade produtiva da Linha de Produção de Placas Eletrônicas, verificando ainda a possibilidade da maximização da margem de contribuição. O principal motivador da realização da pesquisa foi a constatação de que havia um percentual de capacidade de 25% que não estava sendo utilizada, totalizando 720 horas que não eram aproveitadas.

Desta forma, atendendo a esta justificativa, este estudo enuncia o seguinte problema de pesquisa: Como utilizar a capacidade horária disponível para a fabricação das cinco principais placas de forma a obter a otimização conjunta da utilização balanceada da linha de produção e da maximização da margem de contribuição? A partir desta pergunta problema, o objetivo geral do estudo foi otimizar a utilização da capacidade de horas excedentes da linha de produção de placas eletrônicas da empresa. Decorrente deste objetivo geral, pode-se destacar que o objetivo especifico é otimizar a utilização da capacidade produtiva da linha de placas eletrônicas da empresa de forma balanceada, maximizando a margem de contribuição por meio da utilização da programação linear e da otimização multiobjetivo. A próxima seção apresenta a revisão da literatura.

2. Revisão da literatura

2.1 Planejamento e Controle da Produção

O planejamento e controle da produção é a atividade de decidir sobre o melhor emprego dos recursos de produção, assegurando assim a execução do que foi previsto. Autores distintos abordam conceitos convergentes sobre o Planejamento e Controle da Produção. Slack et al. (2002) definem de forma completa e objetiva que o PCP é um conjunto de atividades que conciliam o fornecimento dos produtos e serviços de uma operação com sua demanda, garantindo que os recursos produtivos estejam disponíveis na quantidade, no momento e no nível de qualidade adequada.

Planejamento e controle da produção, segundo Russomano (2000, p.47), "(...) é uma função de apoio de coordenação das várias atividades de acordo com os planos de produção, de modo que os programas pré-estabelecidos possam ser atendidos nos prazos e quantidades desejados". Tubino (2000, p.23) diz que o planejamento e controle da produção "(...) é o responsável pela coordenação e aplicação dos recursos produtivos de forma a atender da melhor maneira possível aos planos estabelecidos em níveis estratégico, tático e operacional".

No contexto do Planejamento e Controle da Produção o planejamento da capacidade tem por objetivo "assegurar a compatibilidade entre a capacidade disponível em centros de trabalho específicos e a capacidade necessária para atender a produção planejada" (FAVARETTO, 2001). Assim entende-se que, identificada a capacidade para atender à demanda futura no momento do planejamento, deverá ser tomada a decisão sobre a adoção de políticas alternativas de suprimento da demanda, caso se faça necessário. Entre as políticas alternativas de suprimento da demanda encontram-se: manutenção da capacidade; acompanhamento da demanda através do ajuste na capacidade; e mudança na demanda existente, de modo a manter a capacidade instalada (SLACK et. al., 2002).

Quanto ao ajuste na capacidade instalada, é necessário a definição dos limites mínimos e máximos da capacidade a ser definida. Esta capacidade será identificada a partir de avaliações de acordo com a demanda futura, sazonalidades ou até mesmo flutuações previstas de ciclos mais curtos, como diários ou semanais. Nestas circunstâncias, o uso da capacidade ociosa, a implantação de novas tecnologias, a adoção de técnicas efetivas de programação e controle, contratação de pessoal ou até mesmo a reorganização do arranjo físico são muitas vezes implantados com o objetivo de aumentar a capacidade (MOREIRA, 1993).

Para Slack et al. (2002), a principal dificuldade na medição de capacidade é a complexidade dos processos produtivos. Somente quando a produção é padronizada e repetitiva, torna-se mais fácil definir a capacidade de maneira precisa. O volume de produção é uma das medidas mais usadas. Porém, quando um número amplo de produtos apresenta demanda variável para o processo, as medidas de volume de produção são menos úteis, baseando-se então na quantidade de insumos, capacidade de máquinas gargalo, entre outros.

Slack et al. (2002), ressaltam que a medida da capacidade deve estar amarrada às restrições dos recursos-chave. Os autores afirmam também que se deve estudar suas características, detalhes relevantes, formas de carregamento e controle, de modo que seja possível converter o mix de produtos em termos de medida de capacidade, e obtenha um resultado compreensível para monitoramento e análise de resultados para viabilizar a tomada de decisões.

Os parâmetros considerados na tomada de decisão do planejamento da capacidade são: unidade de tempo, horizonte de planejamento, nível de agregação dos produtos, nível de agregação das instalações, frequência de replanejamento e níveis de planos antes da implementação. Na procura de um plano de produção de menor custo, Martins e Laugeni (2005) afirmam que um dos métodos mais utilizados é a programação linear, em que a função objetivo a ser minimizada é o custo global do plano. Esta função também pode ser utilizada buscando o lucro máximo no mix de produção analisado. Para Silveira (2008), a programação linear é a técnica mais usada quando se tem problemas e sua modelagem pode ser representada por expressões lineares. Isto porque sua formulação exige que sejam identificadas as variáveis de decisão, função objetivo e as restrições. A programação linear é mais usada para problemas de natureza industrial, bem como na redução de custos e otimização dos recursos disponíveis na empresa, pois a técnica consiste em maximizar ou minimizar algum resultado esperado.

2.2 Pesquisa Operacional e Programação Linear

A Pesquisa Operacional (PO) não possui um marco histórico de origem. Possivelmente, os primeiros problemas que foram resolvidos pela PO surgiram somente após a Revolução Industrial, na segunda metade do século XVIII. Entretanto, o modelo atual da Pesquisa Operacional surgiu durante a Segunda Guerra, tendo sido desenvolvido para resolver problemas militares de ordem estratégica e tática. As raízes da pesquisa operacional remontam a muitas décadas, quando foram feitas as primeiras tentativas para usar uma abordagem científica na gerência das organizações. Entretanto, o início da atividade chamada de pesquisa operacional tem sido geralmente atribuído aos serviços militares no início da Segunda Guerra Mundial (HILLIER, 1988).

A partir do final da Segunda Guerra Mundial, a Pesquisa Operacional se difundiu, passando a ser amplamente utilizada pelas empresas privadas para auxiliar na tomada de decisões. A Programação Linear é uma das técnicas da Pesquisa Operacional que busca a otimização de um determinado problema que possui muitas soluções possíveis, através da maximização ou minimização de uma função linear. Segundo Iudícibus (1998), a programação linear é um instrumento muito utilizado de análise e seleção de alternativas ótimas. Colin (2007) define Programação Linear como um meio para tratar do problema de alocação ótima de recursos escassos para a realização de atividades. Por ótimo supõe-se que não haja outra solução que seja melhor do que a oferecida.

Moreira (2004, p.39) argumenta que "A Programação Linear é um modelo matemático desenvolvido para resolver determinados tipos de problemas onde as relações entre as variáveis relevantes possam ser expressas por equações e inequações lineares". Os problemas de programação linear possuem uma expressão matemática (variáveis de decisão) que devem ser maximizadas ou minimizadas e um conjunto de restrições representadas por equações e inequações, que devem ser atendidas. Segundo Goldbarg e Luna (2005), são três os principais passos a serem seguidos quando da resolução de um problema de programação linear envolvendo otimização de padrões de produção: definição das variáveis de decisão, definição da função objetivo e definição das restrições do sistema em questão.

Quanto ao escopo de aplicação da programação linear, Lachtermacher (2004, p.27) ressalta que esta técnica pode ser utilizada em diversas áreas como: "Administração da produção; Análise de investimentos; Alocação de recursos limitados; Planejamento regional; Logística; Custo de transporte; Localização da rede de distribuição e Alocação de recursos de marketing em diversos meios de comunicação".

Para Taha (2008, p.20), Programação Linear em controle da produção e de estoque pode auxiliar desde a simples alocação na capacidade de máquina para atender à demanda, até o caso mais complexo da utilização de estoque para 'atenuar' o efeito da mudança imprevisível na demanda para determinada projeção de utilização de contratação e demissão para enfrentar as mudanças nas necessidades de mão-de-obra.

Conforme Luche e Morabito (2005), os resultados obtidos da aplicação da programação linear na otimização na programação da produção mostram que os modelos são capazes de gerar soluções melhores do que aquelas que vinham sendo utilizadas pela empresa.

A programação linear é uma das técnicas da pesquisa operacional mais utilizadas em problemas de otimização. Os problemas de programação linear buscam a distribuição eficiente de recursos limitados para atender a um determinado objetivo. A próxima seção trata da otimização multiobjectivo.

2.3 Otimização Multiobjetivo

Assim como a programação linear, a otimização multiobjetivo é realizada a partir de um conjunto de soluções admissíveis definidas por meio de um conjunto de restrições, onde os objetivos são explicitados através da função objetivo (FO). Em geral, nos problemas de otimização multiobjetivo não existe uma solução que otimize simultaneamente todas as FO (ALVES, 2000).

Problemas que demandam a otimização multiobjetivo consistem na otimização de um vetor composto por funções escalares, escolhidas como forma de avaliar o impacto das decisões factíveis do problema, de acordo com diferentes índices de desempenho (OLIVEIRA; FERREIRA, 2003). É importante destacar a mudança no paradigma de otimalidade até então vigente. Na resolução de problemas com um único objetivo, deseja-se encontrar a solução ótima, isto é, que torna máximo ou (mínimo) o valor da FO. É neste ponto que a Programação Multiobjetivo se diferencia dos demais problemas de otimização, ou seja, quanto ao sentido que o conceito de solução do problema assume (STEUER, 1989). Neste caso o conceito tradicional não é mais aplicável, a menos que exista uma solução que otimiza todos os objetivos ao mesmo tempo. Usualmente, é necessário ponderar os objetivos conflitantes e tentar encontrar uma solução de compromisso satisfatória (BUCHANAN; GARDINER, 2003).

A otimização multiobjetivo busca, portanto, encontrar o conjunto de pontos ótimos que são componentes de uma função objetivo vetorial. O vetor é composto pelas várias funções objetivos a serem otimizadas, em que, diferentemente da função mono-objetivo, a solução do problema, é um conjunto de pontos (soluções) eficientes. Cada solução eficiente é ótima no sentido de que nenhuma melhoria pode ser alcançada em um componente da função vetorial sem que haja piora de pelo menos um dos componentes restantes da função vetorial (SHI, 2001). Dentro do conjunto de soluções eficientes o decisor escolherá a que julgue mais satisfatória.

A análise multiobjetivo apresenta conceitos para o tratamento e quantificação dos processos de tomada de decisão com múltiplos objetivos (BRAGA e GOBETTI, 2002). Na análise multiobjetivo não existe um ótimo global, como na busca do máximo ou mínimo de uma função, e sim um conjunto de ótimos que satisfazem, de formas diferentes, os diferentes objetivos envolvidos na análise.

Dependendo da forma em que são utilizadas as preferências do decisor e da natureza do problema, as técnicas de análise multiobjetivo podem ser divididas da seguinte maneira (COHON; MARKS, 1975):

1. Técnicas que geram o conjunto de soluções não dominadas;

2. Técnicas que utilizam uma articulação antecipada das preferências; e

3. Técnicas que utilizam uma articulação progressiva das preferências.

As técnicas que geram o conjunto de soluções não dominadas consideram um vetor de funções objetivos e, mediante tal vetor, geram o conjunto das soluções não dominadas. Uma solução não dominada ou não inferior é definida como uma solução multiobjetivo que não pode ser melhorada em um objetivo sem alterar um ou outros objetivos. Não é considerada no processo as preferências do decisor, tratando-se somente com as restrições físicas do problema. As técnicas que utilizam uma articulação antecipada das preferências solicitam, anteriormente, a resolução do problema, a opinião do decisor a respeito das trocas possíveis entre os objetivos e dos valores relativos destes. As variáveis de decisão podem ser contínuas ou discretas, em função do tipo de problema. Algumas técnicas são aplicadas somente a problemas contínuos ou discretos, enquanto outras podem ser usadas em ambas as situações. As técnicas que utilizam articulação progressiva das preferências têm a característica de perguntar ao decisor, assim que uma solução é alcançada, se o nível atingido de atendimento dos objetivos é satisfatório e, no caso negativo, o problema é modificado e resolvido novamente (BRAGA; GOBETTI, 2002).

A próxima seção apresenta a metodologia.

3. Metodologia

Para o desenvolvimento deste estudo, a metodologia empregada foi operacionalizada por um estudo de caso, a fim de solucionar problemas de várias naturezas, por meio da aplicação de métodos práticos no ambiente em estudo. Referente à natureza da pesquisa, Gil (2002) classifica a pesquisa em básica, quando objetiva gerar conhecimentos novos e úteis para o avanço da ciência, sem aplicação prática prevista; e, aplicada, quando tem o objetivo de gerar conhecimentos para aplicação prática na solução de problemas específicos.

A pesquisa pode ser classificada ou dividida de duas maneiras: a primeira, com base nos procedimentos técnicos utilizados pelo pesquisador, e a segunda se baseia nos objetivos pretendidos. Quanto aos objetivos, a pesquisa pode ser exploratória, descritiva e explicativa. Já quanto aos procedimentos, ela pode ser: bibliográfica, documental, experimental, ex post facto, levantamento, estudo de caso, pesquisa ação e pesquisa-participante. (GIL, 2002).

As pesquisas exploratórias são aquelas que têm como objetivo proporcionar maior familiaridade com o problema, com vistas a torná-lo mais explícito ou construir conjecturas. As descritivas têm como objetivo a descrição das características de determinada população ou fenômeno ou o estabelecimento de relações entre variáveis. As explicativas têm como preocupação central identificar os fatores que determinam ou que contribuem para a ocorrência dos fenômenos, aprofundando mais o conhecimento da realidade porque explica a razão e o porquê das coisas (MARCONI; LAKATOS, 2004).

A coleta de dados ocorreu por meio da observação dos processos, considerando as informações obtidas em planilhas, documentação dos processos e relatórios extraídos do sistema ERP (Enterprise Resource Planning) referentes aos indicadores da empresa objeto de estudo. As informações correspondem ao ano de 2014.

Como procedimento técnico foi utilizado o método do estudo de caso, que possibilita uma visão geral do ambiente. A opção pelo método se justifica devido a interação que os pesquisadores têm com a empresa objeto de estudo. O estudo de caso trata de uma abordagem metodológica de investigação especialmente adequada quando procura-se compreender, explorar ou descrever acontecimentos e contextos complexos, nos quais estão simultaneamente envolvidos diversos fatores. (YIN, 2010).

O estudo tem como objetivo otimizar de forma balanceada a utilização da capacidade produtiva da linha de placas eletrônicas da empresa, maximizando a margem de contribuição por meio da utilização da Programação Linear e da Otimização Multiobjetivo, onde foram avaliados os cinco produtos de maior demanda. Para a aplicação da modelagem matemática foi utilizado o software Microsoft Excel, sendo utilizado em específico o suplemento Solver.

4. Análise dos resultados

4.1 Caracterização da Empresa Pesquisada

O objeto de estudo é uma empresa de pequeno porte que atua no segmento de fabricação de placas de circuito eletrônico, montagens de sinalizações e quadro de controle para elevadores e está situada na cidade de Mogi das Cruzes - SP. A empresa foi fundada no ano de 2002, conta com 90 colaboradores, sendo que a linha de produção de placas eletrônicas (objeto da pesquisa) conta com 15 colaboradores distribuídos ao longo dos processos.

A pesquisa restringe-se apenas a linha de produção de placas eletrônicas, sendo que esta linha é responsável em produzir placas tanto para clientes internos, tais como as linhas de montagem de sinalizações e quadro de controle de elevadores, como para clientes externos, sendo estes tanto fabricantes de elevadores quanto fabricantes de soluções destinados ao seguimento de telecom.

4.2 Coleta de Dados

Os dados coletados basearam-se nos indicadores de desempenho da empresa contemplando o ano de 2014. Esses indicadores refletem informações relacionadas a demanda, custo e preço de venda de cada item. Os relatórios foram extraídos do sistema ERP e as informações foram tabuladas em planilhas do Microsoft Excel e analisadas posteriormente. Para esta pesquisa, foram analisados apenas os cinco principais itens provenientes da Linha de Produção de Placas Eletrônicas, utilizando como critério de escolha a margem de contribuição e a demanda dos itens, sendo que para a demanda foi considerada a média mensal do ano de 2014. A Tabela 1 apresenta a relação dos cinco principais produtos da linha de produção de placas eletrônicas.

Tabela 1: Relação dos cinco principais produtos da Linha de Produção de Placas Eletrônicas.

Fonte: Dados coletados do sistema ERP da empresa.

Também foram coletados os dados dos processos produtivos, onde foram consideradas todas as etapas dos processos de fabricação para as 5 placas que foram analisadas, conforme fluxograma de processo apresentado na Figura 1:

Figura 1: Fluxograma do processo de fabricação de placas eletrônicas, contemplando processos para componentes em SMD - Surface Mounting Device e PTH - Pin Through Hole.
Fonte: Elaborado pelos autores.

Foram analisadas as OMs – Ordem de Montagem dos cinco itens relacionados para o estudo, onde foram observados os tempos de execução de cada atividade ligada ao processo de fabricação. Desta forma foi possível obter dados, que foram tabulados em planilha, onde foram registrados o tempo de fabricação de cada um dos cinco itens. Uma particularidade também observada nas ordens de montagem é que a quantidade do lote mínimo era de 100 peças, onde devido a esta particularidade, os cálculos foram elaborados de forma a considerar o tempo de processo de produção para os lotes de 100 peças. A Tabela 2 apresenta a tabulação dos tempos de execução dos processos em relação aos cinco itens do estudo.

Tabela 2: Relação dos tempos de processo contemplando a fabricação das cinco placas.

Fonte: Dados coletados dos documentos de apontamento de produção da empresa.

Como pôde ser observado na Tabela 2, não são todos os processos que são utilizados na fabricação destas cinco placas, onde as placas 2, 4 e 5 não passam pelos processos de inserção de componentes SMD e solda no forno de refusão. Já as placas 1 e 3 não passam pelos processos de conferência e pré-formação dos componentes PTH, inserção de componentes PTH e solda por onda na máquina.

A capacidade da Linha de Produção de Placas Eletrônicas também foi avaliada, sendo que foram realizados cálculos considerando a quantidade de colaboradores por processo e a carga de hora máquina contemplando os dias disponíveis para trabalho durante o mês, seguindo o conceito de dimensionamento da capacidade conforme Slack et al. (2002).

A empresa objeto do estudo dispõe apenas de um único turno de trabalho, sendo que a jornada de trabalho compreende de Segunda à Sexta Feira, contemplando 44 horas semanais. Os cálculos para dimensionar a capacidade produtiva atual da empresa foram realizados considerando os 20 dias úteis mensais e são exibidos na Tabela 3, determinando assim a capacidade dos processos.

Tabela 3: Capacidade de Produção da Linha de Placas Eletrônicas.

Fonte: Elaborado pelos autores.

Conforme pode-se observar na tabela acima, a Linha de Produção de Placas Eletrônicas possui uma capacidade mensal de 2880 horas considerando todos os processos. Foram realizados cálculos para identificar a carga de horas utilizadas pela linha. Para realizar esta análise, foi considerada a demanda média mensal do ano de 2014, onde foi utilizada a fórmula da Equação 1.

A Tabela 4 ilustra os cálculos e a carga horária utilizada pela linha.

Tabela 4: Carga Horária Utilizada Pela de Linha de Placas Eletrônicas.

Fonte: Dados coletados do sistema ERP da empresa.

Após a verificação da capacidade da linha e da carga horária utilizada, foi realizado um cálculo para determinar o percentual de aproveitamento efetivo da linha. A Tabela 5 apresenta esse cálculo.

Tabela 5: Percentual de Aproveitamento da Capacidade de Horas da Linha de Produção de Placas Eletrônicas.

Fonte: Dados coletados do sistema ERP da empresa.

Observa-se na Tabela 5 que há um aproveitamento da capacidade da linha de 75%. Portanto, a linha de produção de placas eletrônicas têm 25% de sua capacidade que representam 720 horas não aproveitadas. Assim, esse estudo se propõe a encontrar a melhor utilização e otimização para alocar a produção das cinco placas de forma que aproveitem as 720 horas, maximizando a margem de contribuição da linha de produção de placas eletrônicas, procurando equilibrar as quantidades das cinco placas. Os 25% da capacidade que não são utilizados foram estratificados, divididos de forma proporcional respeitando as características peculiares a cada processo. A Tabela 6 apresenta o equivalente de horas por processo em relação aos 25% da capacidade que não são utilizados.

Tabela 6: Horas por processos correspondentes aos 25% da capacidade que não são utilizados.

Fonte: Elaborado pelos autores.

4.3 Análise dos dados

Para a resolução do problema foi elaborada uma modelagem multiobjetivo, buscando otimizar a utilização da capacidade das horas disponíveis, maximizar a margem de contribuição das cinco placas e equilibrar a produção à proporção de demanda histórica.

Para atender aos objetivos foram elaborados 3 modelos representados pelas equações 2, 3 e 4:

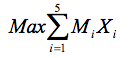  (2)

O primeiro modelo tem como função objetivo maximizar a margem de contribuição, considerando as variáveis de decisão (quantidade de peças a serem produzidas), as restrições impostas para este modelo contemplam a capacidade de horas disponíveis para a execução dos processos e a quantidade de peças a se produzir.

    (3)

O segundo modelo tem como função objetivo maximizar a utilização da capacidade em horas disponíveis, considerando as variáveis de decisão (quantidade de peças a serem produzidas), as restrições impostas para este modelo contemplam a capacidade de horas disponíveis para a execução dos processos e a quantidade de peças a se produzir.

   (4)

O terceiro modelo tem como função objetivo minimizar a proporção em relação ao equilíbrio das quantidades a ser produzida para cada item, onde a variável de decisão permanece nas quantidades de peças que serão definidas pelo cálculo, as restrições para esse modelo compreendem a capacidade de horas disponíveis para a execução dos processos, a quantidade de peças a se produzir e a somatória da quantidade de peças que deve ser igual a maximização encontrada nos modelos 1 e 2.   

Os modelos apresentados ficaram sujeitos as seguintes restrições:

Quantidade de placa a ser produzida deve ser maior ou igual a zero.

A somatória das horas utilizadas para a execução dos processos deve ser igual ou menor que a capacidade de horas disponíveis.

 (Apenas para o modelo 3).

A somatória das quantidades de peças produzidas contemplando todas as cinco placas deve ser igual a maximização obtida nos modelos 1e 2.

Em que:

M=Margem de contribuição

X= Quantidade de placa a ser produzida

i= Placa 1, ..., 5;

a= Coeficiente do processo (em horas)

j= Processo 1, ..., Processo 10

b= Capacidade total do processo em horas

p=Proporção de demanda da placa

A Tabela 7 apresenta os resultados obtidos com os modelos delineados.

Tabela 7: Resultados obtidos com a aplicação dos três modelos matemáticos.

Fonte: Elaborado pelos autores.

Pode-se observar na Tabela 7 os resultados obtidos por meio da aplicação dos três modelos matemáticos utilizados. Cada modelo apresenta resultados distintos para os objetivos analisados, sendo que para a margem de contribuição o melhor resultado foi obtido no modelo 1 com R$ 29.345,32 de lucro. Para o percentual de utilização, o melhor resultado foi obtido no modelo 2 com 79,94%, e para a proporção EQM (Erro Quadrado Médio) e quantidades de peças a serem produzidas o melhor resultado foi obtido no modelo 3.

Definidos os resultados dos três modelos aplicados, o passo seguinte foi aplicar a modelagem multiobjetivo, elaborando uma função objetivo com uma combinação ponderada dos modelos individuais aplicados na forma de desvio percentual em relação ao ótimo obtido em cada modelo conforme demonstrado na Equação 5.

(5)

Implementa-se esse objetivo estabelecendo uma variável MINIMAX Q, que minimizará o desvio percentual máximo ponderado dos valores-alvo para as metas. O modelo revisado para o problema figurará da seguinte forma:

MIN : Q

Sujeito a:

Em que:

w1, w2, w3 são constantes positivas

O modelo final resultou nos valores exibidos na Tabela 8:

Tabela 8: Resultados obtidos com a aplicação do modelo matemático multiobjetivo.

Fonte: Elaborado pelos autores.

5. Discussão dos resultados

Os resultados obtidos neste estudo corroboram com Luche e Morabito (2005), onde os autores demonstram a eficácia da aplicação da programação linear na otimização da programação da produção, mostrando que os modelos são capazes de gerar soluções melhores do que aquelas que vinham sendo utilizadas pela empresa. O modelo de otimização multiobjetivo foi essencial para obter a solução para o problema, para atender aos objetivos propostos neste estudo, a aplicação do modelo multiobjetivo procedeu conforme (BUCHANAN; GARDINER, 2003) que ressaltam que é necessário ponderar os objetivos conflitantes e tentar encontrar uma solução de compromisso satisfatória. 

Os resultados obtidos com a modelagem multiobjetivo e as discussões dos mesmos de acordo com as hipóteses levantadas foram:

a) Otimização da capacidade excedente para a produção das 5 placas de maior demanda:

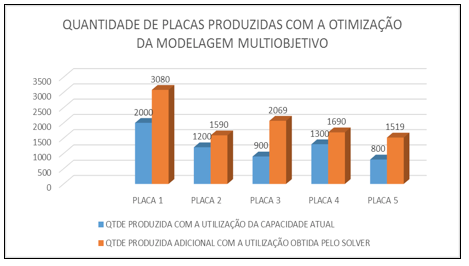
Figura 3: Quantidade de placas produzidas com a otimização da modelagem multiobjetivo.
Fonte: Elaborado pelos autores.

A Figura 3 apresenta um comparativo entre a quantidade de placas produzidas com a utilização atual da capacidade da linha (utilização de 75%), e o acréscimo das quantidades de cada placa, que podem ser produzidas de acordo com os resultados da modelagem obtida pelo solver (os 75% já utilizados mais o adicional que podem ser produzidos com a capacidade excedente de 25%). Estes resultados corroboram a hipótese delineada onde foi possível dimensionar a capacidade excedente da linha de produção de placas eletrônicas de forma balanceada para os 5 principais itens fabricados. Esse fato ocorreu porque a modelagem utilizada considerou que a maior produção deveria se concentrar na placa 1 que é o item de maior demanda da empresa. Com exceção da placa 3, onde a modelagem realizada considerou uma produção de 1.169 peças a maior, o que não condiz com a demanda deste item, a otimização das demais placas obtiveram um resultado balanceado da linha. O resultado divergente da demanda da placa 3 pode ter sido consequência da margem de contribuição deste item que é de R$ 9,20 por peça, ou seja, é o item que apresenta a maior margem de contribuição unitária. Entretanto, este resultado ressalta que a área de marketing da empresa deveria trabalhar de forma a contribuir com o aumento da demanda para a placa 3, pois é o item que apresenta o menor custo unitário para ser produzido e é o que apresenta a melhor margem de contribuição.

b) Maximização da Margem de Contribuição:

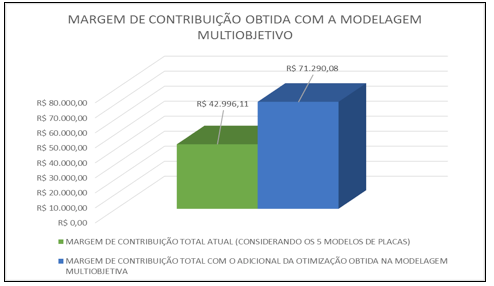
Figura 4: Margem de contribuição obtida com a modelagem multiobjetivo.
Fonte: Elaborado pelos autores.

A Figura 4 compara a margem de contribuição total das 5 placas (margem de contribuição mensal em relação a demanda média mensal de 2014), somados com o resultado obtido pela modelagem multiobjetiva que apresentou uma margem total de R$ 28.293,97 para as 5 placas. Este resultado demonstra que a empresa está deixando de auferir margem de cerca de R$ 28.293,97 mensais por não utilizar a capacidade excedente de 25% da linha de placas eletrônicas. Entretanto, o resultado obtido com a modelagem que utilizou a função MINIMAX Q, que minimizou o desvio percentual máximo ponderado dos valores-alvo para as metas, não foi necessariamente a maior margem de contribuição encontrada. Isto porque, de acordo com os resultados apresentados na Tabela 7, das 3 modelagens realizadas, o primeiro modelo matemático obteve uma margem de contribuição de R$ 29.345,32, que é maior que o resultado obtido com a modelagem multiobjetiva. Contudo, o resultado obtido com a modelagem multiobjetiva foi modificado porque a modelagem utilizada precisava otimizar de forma conjunta a quantidade a ser produzida de cada placa, a margem de contribuição e a utilização balanceada da linha. Isto significa que o resultado obtido foi o que apresentou a melhor otimização para a maximização da margem de contribuição, juntamente com os outros dois objetivos a serem alcançados.

c) Otimização da utilização da capacidade total de horas, considerando os 25% da carga de horas otimizadas no modelo multiobjetivo.

Figura 5: Utilização dos processos da capacidade excedente de 25% obtida com a modelagem multiobjetiva.
Fonte: Elaborado pelos autores.

A Figura 5 compara a capacidade disponível de horas em relação aos 25% de capacidade excedente, e a quantidade de horas utilizadas desta capacidade que a modelagem multiobjetiva utilizou. Conforme demonstra o gráfico, nos processos 2, 5 e 6 foram utilizadas 100% das horas disponíveis, e o processo 9 também utiliza quase 100% de sua capacidade. Nos processos 4, 7 e 10 ainda há quase a metade da capacidade de horas disponíveis que não foram utilizadas. Conforme o resultado obtido com a modelagem multiobjetiva, dos 25% de horas excedentes que estão disponíveis na capacidade da linha, o percentual de utilização é de 79,16%.

Isto significa que dos 25% de horas excedentes, a modelagem realizada conseguiu obter uma otimização onde é possível aproveitar 20% dos 25% excedentes (pois 79,16% do percentual de utilização dos 25% de horas excedentes corresponde a 20%, o que significa que haverá apenas 5% de horas excedentes que ainda restarão da capacidade total da linha de placas eletrônicas). A Tabela 9 compara os cenários anterior e posterior ao da aplicação do modelo.

Tabela 09: Resultados obtidos com a otimização, comparando os cenários anterior e posterior a aplicação do modelo.

Fonte: Elaborado pelos autores.

Pode-se observar na Tabela 9 na Figura 6 que o modelo de otimização multiobjetivo propõe um aumento de 20% quanto ao aproveitamento da utilização da capacidade total da linha de placas eletrônicas, passando da condição inicial de 75% de utilização das horas disponíveis para 95%, sendo esta otimização conciliada ao balanceamento da linha. 

Figura 6: Utilização da capacidade total da linha com a modelagem multiobjetiva.
Fonte: Elaborado pelos autores.

A próxima seção apresenta as considerações finais.

6. Considerações finais

Os resultados obtidos com esta pesquisa atenderam aos objetivos almejados com a a aplicação do modelo matemático proposto, onde foi possível otimizar de forma conjunta a quantidade de placas a serem produzidas com a capacidade de horas excedentes da linha de produção de maneira a obter uma utilização balanceada, além de maximizar a margem de contribuição dos itens.

As limitações deste estudo compreenderam apenas a análise das 5 principais placas da linha, que são os itens de maior demanda do estudo de caso. Outra limitação refere-se aos tempos de processo para os demais itens produzidos nesta linha, onde o tempo em horas apresentado foi extraído do relatório de produção, sendo contabilizado na sua totalidade e não de forma individual. Apesar destas limitações, os resultados obtidos com a modelagem realizada reforçam que a empresa poderia auferir cerca de R$ 28.293,97 na margem de contribuição mensal. Os resultados também indicam a possibilidade de aumento quanto a utilização da capacidade da linha passando de 75% para 95%, propondo 20% a mais de utilização da linha.

Como contribuição deste estudo, pode-se ressaltar as melhorias nos processos produtivos das empresas com a aplicação de técnicas de modelagem matemática proporcionando ganhos tanto produtivos como financeiros, além de demonstrar os processos passíveis de melhorias. Este estudo também contribui ressaltando a importância das ferramentas de pesquisa operacional como subsídio para a tomada de decisão na gestão de produção, além de propor novas pesquisas a fim de conciliar as melhorias da capacidade produtiva obtida com a otimização da modelagem matemática com o planejamento de marketing, onde se faz necessária a prospecção de demanda para utilizar de maneira eficiente a capacidade excedente e de todos os recursos disponíveis da empresa.

Referências bibliográficas 

ALVES, Maria João Teixeira Gomes, (2000). "Apoio À Decisão em Problemas de Programação Inteira e Inteira-Mista Multiobjetivo: Contribuições Metodológicas", Tese de Doutorado, Faculdade de Economia. Universidade de Coimbra.

ANDRADE, M.M. Introdução à metodologia do Trabalho Científico: Elaboração de Trabalhos de Graduação. São Paulo: Atlas, 1993.

BRAGA, B.; GOBETTI, L. (2002). Analise Multiobjetivo. In: Técnicas Quantitativas para o Gerenciamento de Recursos Hídricos. 2ª Edição. Editora da Universidade/UFRGS–ABRH. Porto Alegre, p. 361-420.

BRAVO, J. M., COLLISCHONN, W., PILAR, J. V. (2005). Otimização da Operação de Reservatórios: Estado-da-Arte. In: XVI Simpósio Brasileiro de Recursos Hídricos. João Pessoa.

BUCHANAN, J., Gardiner, L. (2003). "A Comparation of Two Reference Point Methods In Multiple Objective Mathematical Programming" EJOR, 149, 17-43.

CLÍMACO, João Namorado, Antunes, Carlos Henggeler, Alves, Maria João Gomes, (2003). Programação Linear Multiobjetivo. Coimbra, Imprensa Universidade.

COHON, J. L.; MARKS, D. H. (1975). A Review and Evaluation of Multiobjective Programming Techniques. Water Resources Research, v. 11, n. 2. p. 208-220.

COLIN, Emerson C. Pesquisa Operacional. Editora: LTC, 2007.

CORRAR, Luis João; GARCIA, Editinete A. da Rocha. Programação linear: uma aplicação à contabilidade de custos no processo de tomada de decisão. In: CONGRESSO INTERNACIONAL DE CUSTOS, 7, 2001, León. Disponível em http://www.intercostos.org/documentos/Trabajo066.pdf.

DODGE, Mark e STINSON, Craig. Microsoft Excel 2000 – Guia Autorizado. São Paulo: Makron Books, 2001.

FAVARETTO, Fábio. Uma contribuição ao processo de gestão da produção pelo uso da coleta automática de dados de chão de fábrica. Tese (Doutorado em Engenharia Mecânica) – Escola de Engenharia de São Carlos. USP, São Paulo, 2001.

FONSECA, J. J. S. Metodologia da pesquisa científica. Fortaleza: UEC, 2002. Apostila.

GIL, Antonio C. Como Elaborar Projetos de Pesquisa. São Paulo: Atlas, 2002.

GOLDBARG, Marco Cesar e LUNA, Henrique Paccal. Otimização combinatória e programação linear: modelos e algoritmos. 2.ed. Rio de Janeiro: Elsevier, 2005.

GOMES, L. F. A. M., Gomes, C. F. S., Almeida T., Adiel, (2006). Tomada De Decisão Gerencial O Enfoque Multicritério. Editora Atlas, São Paulo, Segunda Edição. Brasil.

HILLIER, F. S. Introdução a pesquisa operacional. Rio de Janeiro: Campus, 1998.

IUDICIBUS, S. de. Contabilidade Gerencial. 6a ed. São Paulo: Atlas, 1998.

KUHNEN, Osmar Leonardo. Métodos quantitativos. Erechim: Apostila da Pós-Graduação em Auditoria e Perícia, 2002.

LABADIE, J. W. (2004). Optimal Operation of Multireservoir Systems: State-Of-The-Art Review. Journal of Water Resources Planning and Management. v. 130. n. 2, p. 93-11.

LACHTERMACHER, Gerson. Pesquisa Operacional na Tomada de Decisões. 2. ed. Rio de Janeiro: Campus, 2004. 384 p.

LUCHE, José Roberto Dale e MORABITO, Reinaldo. Otimização na programação da produção de grãos eletrofundidos: um estudo de caso. Gestão & Produção. São Carlos, v. 12, n. 1, p.135-149. jan./abr.2005.

MARCONI, Marina A.; LAKATOS, Eva M. Metodologia Científica. São Paulo: Atlas, 2004.

MARTINS, P. G.; LAUGENI, F. P. Administração da produção. São Paulo: Saraiva, 2005.

MICROSOFT OFFICE On-Line - Sobre o Solver. Disponível em: <http://office.microsoft.com> Acesso em: 05 de junho de 2015.

MOREIRA, Daniel A. Administração da Produção e Operações. São Paulo: Pioneira, 1993.

MOREIRA, Daniel Augusto. Administração da Produção e Operações. São Paulo: Pioneira Thomson Learning, 2004.

OLIVEIRA, Rubia M., Ferreira, Paulo A. V., (2003). Programação Geométrica Multiobjetivo: Uma Implementação Computacional Via Matlab, XXXV Sbpo, Natal, Pág, 2204-2216.

RUSSOMANO, Victor Henrique. Planejamento & Controle da Produção. 6. ed. São Paulo: Pioneira, 2000.

SHI, Yong, (2001). Multiple Criteria and Multiple Constraint Levels Linear Programming, Concepts, Techniques & Applications. World Scientific. N.Y.

SILVEIRA, Carlos Augusto. Pesquisa operacional no ensino da logística. Santa Catarina: Artigo Científico, 2008.

SLACK, Nigel; CHAMBERS, Stuart; JOHNSTON, Robert. Administração da produção. 2. edição. São Paulo: Atlas, 2002.

STEUER, Ralph E., (1989), Multiple Criteria Optimization: Theory, Computation And Application. Robert E. Krieger Publishing Company, Inc.

STEUER, Ralph E., Gardiner, Lorraine R., (1994), Unified Interactive Multiple Objective Programming. European Journal of Operational Research, Pp. 391-406.

TAHA, Hamdy A. Pesquisa Operacional. 8.ed. São Paulo: Pearson Prentice Hall, 2008.

TUBINO, Dalvio Ferrari. Manual de planejamento e controle da produção. 2. ed. São Paulo: Atlas, 2000.

WINSTON, Wayne L. Introdução à otimização com a ferramenta Solver do Ms-Excel. Disponível em: <http://Office.microsoft/pt-br/assistance/hp051983681045.aspx>. 2004. Acesso em: 05 de junho de 2015.

YIN, R.K. Estudo de caso: planejamento e métodos. 4ª ed. Porto Alegre: Bookman, 2010.

1. Formado em 2009 no curso Superior de Gestão da Qualidade e Produtividade pela Universidade Mogi das Cruzes - UMC, Formado em 2011 no Curso Técnico de Projetos Mecânicos pela ETEC Presidente Vargas - Centro Paula Souza. Pós-Graduando no curso Lato Senso de Logística e Operações  IFSP – Suzano. E-mail: eduardo.dassan@hotmail.com
2. Graduada em 2010 no curso de Administração de Empresas pela Faculdade Unida de Suzano - Unisuz, e pós-graduada em 2015 no curso de Logística e Operações pelo IFSP.  E-mail: daya.santos26@hotmail.com
3. Graduado em Administração de Empresas pela Faculdade do Litoral Sul Paulista (2005), mestrado em Gestão de Negócios pela Universidade Católica de Santos (2008) e doutorado em Administração pela FEA/USP em 2015. Atualmente é professor do Instituto Federal de São Paulo - Câmpus Suzano. E-mail: adrianoms@ifsp.edu.br

4. Doutor em Engenharia Biomédica; Mestre em Tecnologia Ambiental; MBA em Tecnologia da Informação Aplicada à Gestão de Negócios; Especialista em Informática na Saúde; Tecnólogo em Informática; e Bacharel em Administração de Empresas.. E-mail: luizteruo@hotmail.com

5. Graduado em Administração de Empresas (2000), Mestrado em Engenharia de Produção (2003) e Doutorado em Engenharia de Produção (2012). E-mail: eniofr@uol.com.br