Espacios. Vol. 37 (Nº 20) Año 2016. Pág. E-4

Geogebra no ensino de Cálculo Diferencial e Integral I

Geogebra in teaching of Differential Integral Calculus I

Renato HALLAL 1; Liliane HELLMANN 2; André SANDMANN 3; Andriele de Pra CARVALHO 4; Francisco REINALDO 5; Celso HOTZ 6

Recibido: 14/03/16 • Aprobado: 29/03/2016

Conteúdo

1. Introdução

2. Revisão de Literatura

3. Metodologia

4. Resultados e Discussões

5. Considerações Finais

Referências

1. Introdução

Participando diretamente do mundo acadêmico, nota-se que é cada vez maior o empenho do docente para ensinar seus alunos de maneira lúdica e prazerosa o conteúdo matemático, devido ao histórico de alunos terem dificuldade a entender essa disciplina.

As disciplinas de Matemática são consideradas pelos alunos, mesmo por aqueles que frequentam cursos da área de ciências exatas, como sendo as mais difíceis de suas grades curriculares e, como consequência desta dificuldade, são elas as que geram maiores índices de reprovação.

Em particular, nas universidades, a disciplina de (CDI-I), proposta no primeiro semestre dos cursos tem sido a principal protagonista desses elevados índices de reprovações e evasões estudantis.

No entanto, observa-se que o ensino da matemática tem enfrentado dificuldades no que diz respeito ao seu ensino/aprendizagem. Encontra-se, na literatura, estudos que buscam entender as razões dessas dificuldades e, ao mesmo tempo, encontrar alternativas que possam contribuir para a aprendizagem dos conteúdos estudados nessas disciplinas (CURY, 2006; FERREIRA & BRUMATTI, 2009 e SILVA & FERREIRA, 2009).

Muitos pesquisadores, como Santos, Costa, Godoy e Busquini (2011) consideram que as políticas curriculares endossam a visão de certos grupos de especialistas e que a educação secundária transita pela dualidade propedêutico-profissionalizante. Essa visão configura-se pela estruturação dos currículos das diferentes disciplinas em termos de competências como contraposição à estruturação dos currículos por objetivos de conteúdos específicos. No entanto, o cenário secundário brasileiro segue marcado pelos programas dos exames vestibulares, das principais Universidades Brasileiras do país, bem como pelo ENEM, que acabam por ter uma função indutora e reguladora do currículo do Ensino Médio. Em particular, no que se refere ao currículo de Matemática para o Ensino Médio que, por mais que se façam recomendações curriculares a partir de referenciais teóricos e pesquisas, estas nunca são consideradas, prevalecendo sempre a listagem de conteúdos matemáticos determinados pelos exames vestibulares.

No ensino superior, na disciplina de CDI-I, essas dificuldades estão explicitas, por apresentar um considerável grau de abstração e a necessidade de representações gráficas e/ou algébricas.

Deste modo, Cury (2006), Ferreira & Brumatti (2009) e Silva & Ferreira (2009) afirmam que o uso de softwares computacionais aplicados, possibilitam uma inovação no ensino, pois são considerados uma ferramenta auxiliar na construção de conceitos e aplicações relacionados ao ensino de matemática, o que permite criar situações de aprendizagem estimulante. Além disso, o uso dessas ferramentas pode viabilizar a construção do conhecimento, de maneira autônoma e independente.

Assim, sentiu-se a necessidade de uma nova maneira de interpretar e trabalhar com os conteúdos propostos na disciplina em questão, sem contudo, desconsiderar o grau de complexidade e os níveis de qualidade requeridos pela universidade.

Diante do exposto, buscou-se neste trabalho, uma alternativa para o estudo de funções, limites, derivadas e integrais, com o auxílio do computador, em particular, do software Geogebra. Nessa perspectiva, desenvolveu-se um material de apoio composto de vários exercícios resolvidos, a fim de auxiliar os alunos a retomar o conteúdo de CDI-I, e também, aprender uma nova linguagem, utilizando os recursos computacionais para facilitar a compreensão de diversos conceitos desta disciplina.

2. Revisão de Literatura

A introdução da Informática na Educação, segundo a proposta de mudança pedagógica, exige formação bastante ampla e profunda dos educadores. Não se trata de criar condições para o professor simplesmente dominar o computador ou o software, mas sim, auxiliá-lo a desenvolver conhecimento sobre o próprio conteúdo e sobre como o computador pode ser integrado no desenvolvimento desse conteúdo. Nesse enfoque, a questão da formação do professor mostra-se de fundamental importância no processo de introdução da Informática na Educação, exigindo soluções inovadoras e novas abordagens que fundamentem os cursos de formação (VALENTE, 2005).

Na atual conjectura, em que se encontra a educação, em especial o ensino da Matemática (levando-se em consideração a precariedade da formação de muitos profissionais da educação), a utilização de computadores e seus recursos e softwares (jogos, multimeios, sistemas virtuais de aprendizagem, vídeo aulas), no processo de Ensino e Aprendizagem, é muito mais diversificada, interessante e desafiadora, do que simplesmente a de transmitir informação ao aprendiz. O computador pode ser também utilizado para enriquecer ambientes de aprendizagem e auxiliar o aprendiz no processo de construção do seu conhecimento.

"O quadro-negro não deixa de ser uma tecnologia importante, sobretudo para o professor de Matemática, que o utiliza para interagir com a turma e o conteúdo, seja na demonstração de um teorema, ou mesmo na apresentação das soluções para as várias questões trabalhadas, mas todos haverão de concordar que esse ambiente se mostra extremamente limitado na abordagem de algumas situações matemáticas." (ROCHA, SANTIAGO, LOPES, DANTAS e NETO, 2007)

Desta maneira, torna-se imprescindível a mobilização dos educadores em compreender o significado e as consequências do uso das novas tecnologias no ambiente acadêmico. Para isso, estudos e pesquisas têm refletido sobre essa prática pedagógica, que está sendo exigida das escolas/universidades e que vem desenhando uma relação professor/aluno/conteúdo/tecnologia. A essa relação, somam-se as novas Tecnologias da Informação e Comunicação (TICs).

2.1. Tecnologia de Informação e Comunicação

A União Europeia assinala que Tecnologia de Informação e Comunicação (TICs), é um termo adotado para referenciar serviços, aplicações e tecnologias, que empregam diversos tipos de equipamentos e de softwares, que podem ser (também) transmitidos por meio das redes de telecomunicações (BRUM & MOLERI, 2010).

As TICs são utilizadas nas mais diversas formas, na indústria (no processo de automação), no comércio (no gerenciamento, nas diversas formas de publicidade), no setor de investimentos (informação simultânea, comunicação imediata) e na educação (no processo de ensino-aprendizagem).

Uma das áreas mais favorecidas com as TICs é a educacional. Na educação presencial, as TICs são vistas como potencializadoras dos processos de ensino-aprendizagem. Além disso, a tecnologia traz a possibilidade de maior desenvolvimento, aprendizagem e comunicação entre as pessoas (NEVES, 2003).

Segundo Allevato (2005; 2010), importantes pesquisas já foram e estão sendo desenvolvidas, buscando compreender as implicações e formas de implementação da resolução de problemas no ensino de Matemática. Os problemas sempre ocuparam, invariavelmente, um lugar de destaque no ensino e nos currículos de Matemática, entretanto a finalidade e outros aspectos relacionados à resolução de problemas passaram por mudanças. Essas mudanças ocorreram, principalmente, buscando acompanhar as diferentes visões sobre o porquê de se ensinar Matemática e, particularmente, de trabalhar com resolução de problemas em sala de aula. Algumas reflexões têm voltado para a forma como a resolução de problemas está associada a outros recursos e elementos considerados na Educação Matemática: aos jogos, à modelagem, aos projetos, às TICs, entre outras. A esta última, especificamente ao computador, é que está voltado o presente texto.

2.2. A importância dos computadores na educação matemática

A utilização da tecnologia, especialmente a do computador, pode ser encarada como colaboradora na sala de aula, pois permite tratar de problemas diversos, que envolvem diferentes níveis de complexidade algébrica e grande quantidade de dados. Ela é facilitadora, já que, ao possibilitar uma ampla visualização de imagens, contribui, tanto para a melhor aprendizagem de conceitos, quanto para aplicações da Matemática. Além disso, a utilização do computador pode colaborar para suprir as exigências do mercado de trabalho, que requer cada vez mais do profissional, com uma formação generalista, crítica e reflexiva.

Silva & Ferreira (2009), reconhecem que a utilização do computador, com a finalidade de explorar ideias matemáticas, pode provocar a mudança do ambiente da sala de aula centrada no professor para um alunado que é levado a refletir sobre as informações recebidas, já que o computador possibilita a simulação de diversas situações. O computador pode ser considerado como um meio de aprender fazendo, pensando e argumentando, de forma que a interação seja o ponto chave.

Valente (2005) salienta que o uso do computador na educação, objetiva a integração deste no processo de aprendizagem dos conceitos curriculares, em todas as modalidades e níveis de ensino, podendo desempenhar um papel de facilitador, entre o aluno e a construção do seu conhecimento.

A tecnologia é essencial no processo da visualização e essa por sua vez ocupa um papel fundamental na compreensão de conteúdos matemáticos. Para Arcavi (2003), a visualização pode ser caracterizada como um objeto, uma imagem, e também como um processo, uma atividade. A visualização gráfica mediada pela tecnologia, possibilitada por diversos softwares, tem sido uma alternativa na sala de aula; é mais um caminho (recurso) que pode contribuir para que o aluno tenha uma visão mais ampliada, sobre como usar determinada ferramenta e como direcioná-la para aplicações reais.

A utilização dos recursos computacionais, particularmente na educação, ocupa uma posição central, e por isso é importante refletir sobre as mudanças educacionais provocadas por essas tecnologias, propondo novas práticas docentes e buscando proporcionar experiências de aprendizagem significativas para os alunos.

Ademais, alguns estudos destacam que as possibilidades de representação numérica, algébrica e gráfica que o computador oferece, permite que o aluno aproprie-se de noções visuais que os auxiliam nos processos formais. Cabe salientar que a visualização tem ocupado uma posição de destaque nos estudos referentes à associação do computador ao ensino de Matemática. (BORBA; VILLARREAL, 2005).

Diante deste contexto, esta experiência pretende auxiliar o ensino-aprendizagem de conteúdos matemáticos por intermédio da visualização gráfica do software Geogebra, podendo favorecer o discente na compreensão dos conteúdos matemáticos, bem como estimular o docente em suas atividades pedagógicas.

2.3. O Geogebra

O utilização de novas tecnologias como os softwares educacionais podem auxiliar na solução de problemas encontrados no âmbito educacional desde o ensino fundamental ao superior. Os softwares matemáticos são apresentados como uma nova proposta pedagógica, utilizados para a motivação da aprendizagem e a participação mais ativa do aluno.

O Geogebra é um software matemático livre (para uso não comercial), com base na GPL (GNU General Public License), desenvolvido por Markus Hohenwarter no início de 2001 na University of Salzburg, na Áustria, para ser utilizado em ambiente de sala de aula, tendo continuidade na Florida Atlantic University.

Pelo Geogebra se tratar de um software livre, os colaboradores podem realizar alterações em seus códigos fontes atualizando ou acrescentando novas ferramentas, a fim de disponibilizarem melhoramentos a todos que o utilizem.

Figura 1 - Representação da função f(x) e uma reta tangente a essa curva.

Como forma de ilustrá-lo (Figura 1 - acima), o Geogebra possui a forma de entrada dos comandos bem simples e sua interface é bastante intuitiva, além de possuir formas simples de alterar o zoom, ajustar janelas e mover pontos. O software também permite que sejam feitas animações, o que facilita o entendimento do aluno, quanto a variações que ocorrem com algumas funções.

É possível observar, na Figura 1, que o Geogebra, possui uma janela algébrica, localizada a esquerda da tela e uma janela geométrica da tela, o que facilita a visualização por parte do seu usuário.

3. Metodologia

Para o desenvolvimento desse projeto, realizou-se inicialmente um estudo sobre os principais softwares matemáticos (matlab, winplot, maple, entre outros), a fim de analisar qual o mais adequado no trabalho dos conteúdos da disciplina de CDI-I. Decidiu-se em utilizar o software Geogebra, por ser gratuito e apresentar uma interface simples e de fácil utilização, sendo interativo com o usuário, além de dispor de muitos recursos gráficos voltados aos conteúdos abordados.

Após aprofundar os estudos sobre o software e explorar seus recursos, desenvolveu-se um manual explicativo, com a utilização de suas ferramentas básicas, contendo imagens e explicações passo a passo, aplicados aos conteúdos de funções, limites, derivadas e integrais, os quais fazem parte da grade curricular da disciplina de CDI-I.

Na sequência destacam-se algumas atividades abordadas no manual desenvolvido. O exemplo 1 refere-se a apresentação da reta tangente ao gráfico e no exemplo 2 destaca-se o cálculo da área aproximada através da Soma de Riemann utilizada para introduzir os conceitos de integrais definidas.

Exemplo 1: Software Geogebra na representação gráfica do conceito de derivadas através da função.

Passo 1: Digitar a função na barra de entrada. Verifique a plotagem do gráfico.

Figura 2 – Representação gráfica da função.

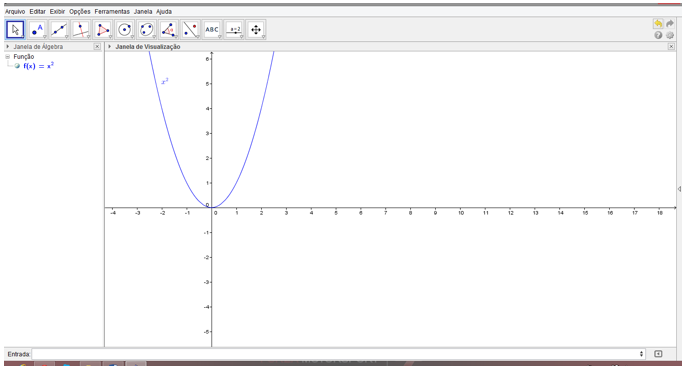
Passo 2: Cria-se um ponto aleatoriamente na função f(x) digitando-se na barra de entrada .

Figura 3 – Representação gráfica da função  e do ponto A.

Este ponto pode ser arrastado para qualquer outra posição ao longo da função f(x).

Passo 3: Adicionar uma reta tangente a função f(x) no ponto , para isso digita-se na linha de entrada entrada t = tangente[A,f].

Figura 4 – Representação gráfica da função  e da reta tangente no ponto A.

Movimentando o ponto  ao longo da função f(x) verifica-se que altera a reta tangente e nota-se, que o coeficiente angular da reta, altera-se de acordo com o ponto.

Exemplo 2: Soma de Riemann.

Soma de Riemann é o nome dado ao processo de calcular uma determinada medida por meio da soma de infinitas parcelas. Podemos calcular a área de uma determinada região subdividindo-a em vários retângulos, e somando-se a área desses retângulos. Quanto mais retângulos usarmos para a decomposição, melhor será a aproximação dessa soma com o valor real da área da região. Vamos entender melhor através do exemplo abaixo considerando uma função.

Passo 1: Digitar a função  na barra de entrada.

Passo 2: Clique na opção "Controle de Deslizante" e em um local qualquer sobre a área gráfica.  

Figura 5 – Representação gráfica da função .

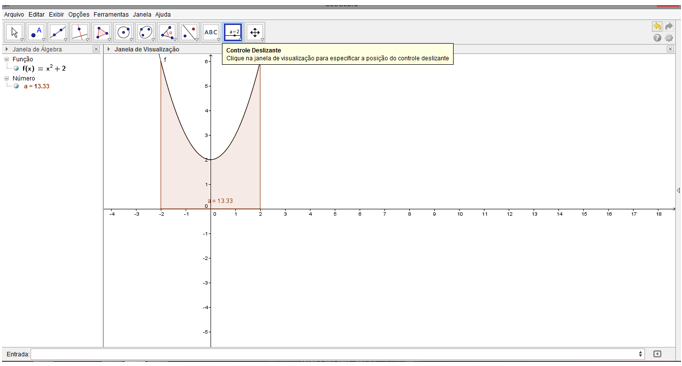
Passo 3: Nos intervalos delimite-os entre 1 a 50, o incremento de 1 e altere o nome para "n".

Figura 6 – Representação gráfica da função  definindo o incremento para n.

Passo 4: Na aba "Controle Deslizante", desmarque a opção "Fixo", altera-se a largura para 300 e clique em "Aplicar".

Figura 7 – Representação gráfica da função aplicando largura 300.

Passo 5: Na barra de entrada digite: SomaDeRiemannInferior [ x^2 + 2, -2, 2, n].

Figura 8 – Representação da Soma de Riemann com 1 retângulo

O comando baseia-se em: SomaDeRiemannInferior[Função, Valor de x Inicial, Valor de x Final, Número de Retângulos], delimitamos os intervalos de "x" e em "Número de Retângulos" colocamos "n" pois será uma variável que movimentaremos ao longo da reta.

Passo 6: Movimenta-se a variável n=1 ao longo da reta, como por exemplo n=11.

Figura 9 – Representação da Soma de Riemann através de 11 retângulos

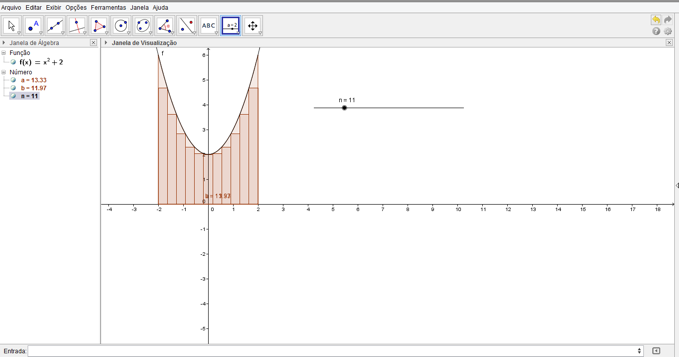
 Passo 7: Aumentando-se n=38.

Figura 10 – Representação da Soma de Riemann através de 38 retângulos.

Verifica-se que quanto maior o valor de n, mais retângulos temos e a área se aproxima do valor exato que pode ser determinada através da integral definida.

Deste modo, disponibilizou-se no manual diferentes atividades que abordam importantes conceitos matemáticos de funções, limites, derivadas e integrais, a fim de auxiliar o acadêmico no entendimento do conteúdo e na sua representação gráfica.

Para a validação do material, apresentou-se, em forma de minicurso, o objetivo de desenvolvimento do material, ferramentas básicas e utilidades do software, a alunos da UTFPR, câmpus Medianeira, que já cursaram a disciplina de CDI-I.

Inicialmente, apresentou-se as ferramentas básicas do software, aplicadas na resolução de problemas dos conteúdos de CDI-I. Enquanto realizava-se a apresentação do manual, os alunos reproduziam no software os comandos necessários e, na sequência, resolveram alguns exercícios individualmente para verificar as dificuldades, bem como as possíveis falhas encontradas. Para alguns exercícios, antes de iniciar a resolução com o auxílio do software, foram resgatados alguns conceitos elementares de matemática, necessários para a interpretação gráfica dos mesmos.

Ao final da apresentação, aplicou-se um questionário a respeito do material, analisando a didática, o entendimento e quais as dificuldades encontradas ao reproduzir no software Geogebra os exercícios propostos no material, além de sugestões para melhoria do mesmo.

4. Resultados e Discussões

A primeira abordagem realizada foi sobre o conhecimento e a utilidade do software, o que uma porcentagem considerável (80%) já ouviu falar, mas nunca teve contato direto com o Geogebra.

Quando questionados a respeito das principais dificuldades enfrentadas na disciplina de Cálculo Diferencial e Integral I, um fator relevante foi à dificuldade na representação gráfica, que julgam que o manual desenvolvido poderia auxiliar nas representações de forma fácil e rápida, sendo útil para a verificação de exercícios resolvidos em sala.

Com as atividades apresentadas, foi possível perceber um bom aceite por parte dos alunos, pois demonstraram entusiasmo ao utilizar o software, além de elogios pela sua praticidade e possibilidade de simulação ao resolver exercícios, além de ser útil na verificação de resoluções feitas manualmente. A seguir, algumas considerações, feita pelos alunos: "é possível verificar o que acontece no gráfico, quando alteramos um número ou um sinal" ou "o Geogebra ajuda a representar e calcular gráficos que demorariam muito tempo para fazer manualmente".

Com relação à abordagem do manual e a utilização do software os alunos julgam importante a utilização de um software no desenvolvimento da disciplina, pois seu uso visa facilitar a visualização gráfica e possibilitam simulações, que de acordo com Gravina e Santarosa (1998), um ambiente educacional informatizado possibilita ao estudante visualizar situações que não seriam possíveis sem o auxílio de um recurso computacional, além de modelar problemas e fazer simulações.

Uma porcentagem considerável (50%) dos alunos enfatiza a importância do uso do software, pois é possível visualizar, por meio da representação gráfica, o que foi resolvido manualmente, se tornando mais fácil o entendimento, o que está de acordo com o exposto com Fonseca e Gonçalves (2010), onde destacam que a utilização de recursos computacionais nas aulas possibilita a exploração dos conteúdos matemáticos, a partir do campo visual do aluno, onde ele utiliza-se de uma imagem e explora o conceito matemático envolvido em uma situação problema.

Algumas dificuldades destacadas pelos alunos referem-se aos comandos utilizados na digitação das funções, mas os mesmos justificam tal dificuldade por não estarem familiarizados e habituados a utilizar o Geogebra.

5. Considerações Finais

Com o desenvolvimento do minicurso e o manual apresentado, os alunos perceberam a importância e utilidade do software Geogebra na disciplina de CDI-I. Por meio dos comentários apresentados pelos alunos, foi possível perceber a necessidade e importância de trabalhar com um ambiente educacional informatizado, não apenas para diversificação do conteúdo mas para proporcionar um conhecimento dinâmico, contribuindo para a compreensão do conteúdo.

O manual proporcionou aos estudantes conhecer o software Geogebra e fazer uso do mesmo, não apenas com a construção de gráficos mas de uma forma investigativa do conteúdo de CDI-I.

Neste contexto, não pode-se deixar faltar a presença do professor e das TICs, pois estas, quando bem integradas e engajadas, contribuem para a construção do conhecimento. A relação professor/aluno/conteúdo/tecnologia, precisa estar fundamentada em teorias, que tenham em mente a emancipação humana, além de ter clareza que as pessoas geralmente constroem conhecimento com base na capacitação, colaboração, participação e inovação.

Propõe-se, para continuidade do projeto, a elaboração de vídeo aulas, a fim de facilitar a utilização do software, tornando-o mais dinâmico, evitando desperdício de tempo para conhecimento dos seus comandos, além da inserção do material no MOODLE, disponibilizando-o para a disciplina de CDI-I na modalidade EaD ofertada pela UTFPR.

Referências

ALLEVATO, N. S. G. Associando o computador à resolução de problemas fechados: análise de uma experiência. Tese (doutorado) – Universidade Estadual Paulista (UNESP). Instituto de Geociências e Ciências Exatas. Rio Claro. 2005.

ALLEVATO, N. S. G. Utilizando animação computacional no estudo de funções. Revista de Ensino de Ciências e Matemática, 2010. Disponível em: http://revistapos.cruzeirodosul.edu.br/index.php/rencima/article/viewFile/13/15. Acessado em 20/03/2014.

ARCAVI, A. The role of visual representations in the learning of mathematics. Education Studies en Mathematics, v. 52, n. 3, p. 215-241. 2003.

BORBA, M. C.; VILLARREAL,M. E. Humans-with-Media and the Reorganization of Mathematical Thinking. EUA: Springer, 2005.

BARANAUSKAS, C. C., D'ABREU, J. V., MARTINS, M. C., & ROCHA, H. V. Uma taxonomia para ambientes de aprendizado baseados no computador. In: J. A. Valente, O Computador na sociedade do conhecimento (pp. 45-69). Brasília: Estação Palavras - USP, 2005.

BORBA, M., & PENTEADO, M. Informática e Educação Matemática. Belo Horizonte: Autêntica, 2007.

CURY, H. N. Análise de erros em disciplinas matemáticas de cursos superiores. III Seminário Internacional de Pesquisa em Educação Matemática, Águas de Lindóia, Anais.. Águas de Lindóia: SBEM, CD-ROM. 2006.

FERREIRA, D. H. L.; BRUMATTI, R. N. M. Um olhar voltado para alunos com dificuldades em Matemática num curso de Engenharia Elétrica. Anais do VI Congresso Iberoamericano de Educación Matemática, Puerto Montt, Chile, p. 949-955. 2009.

FONSECA, D. S. S. de M.; GONÇALVES, D. C. O Uso do GeoGebra no Ensino de Limite. Encontro Nacional de Educação Matemática. Bahia: Anais, 2010.

GRAVINA, M. A., SANTAROSA, L. M. A aprendizagem da matemática em ambientes informatizados.  IV Congresso RIBIE, Brasília, 1998.

NASCIMENTO, E. G. A. do. Avaliação do software Geogebra como instrumento psicopedagógico de ensino em geometria. 112f. Dissertação (Mestrado em Educação) Faculdade de Educação. Universidade Federal do Ceará. Fortaleza, 2012.

NEVES, C. M. C.; Referências de qualidade para cursos à distância. Ministério da Educação. Secretaria de Educação a Distância. Brasília, 2003.

ROCHA, E. M., SANTIAGO, L. M., LOPES, J. O., DANTAS, D. M., & B.NETO, H. Uso da informática nas aulas de Matemática: Obstáculo que precisa ser superado pelo professor, o aluno e a escola. Anais do XXVII Congresso da SBC XIII Workshop sobre informática na escola. Rio de Janeiro, RJ. 2007.

SANTOS, V. P. Interdisciplinaridade na sala de aula. São Paulo: Loyola, 2007.

SANTOS, V., COSTA, J. C.; GODOY, E.; BUSQUINI, J. A. Ensino Médio e Ensino de Matemática: Vocação, Orientações Curriculares e Perspectivas. Texto produzido atendendo à solicitação do Grupo de Trabalho de  Educação Matemática da ANPED, 2011.

SILVA, J. I. G.; FERREIRA, D. H. L. O uso de tecnologias na disciplina de cálculo diferencial e integral I. Anais do XIV Encontro de Iniciação Científica da PUC-Campinas. 29 e 30 de setembro de 2009.

VALENTE, J. A. O computador na sociedade do conhecimento. Brasília: Estação Palavra - USP. 2005.

1. Prof. Mestre, Universidade Tecnológica Federal do Paraná/UTFPR. E-mail: renatohallal@utfpr.edu.br
2. Prof. Mestre, Universidade Tecnológica Federal do Paraná/UTFPR. E-mail: lilianehellmann@utfpr.edu.br
3. Prof. Doutor, Universidade Tecnológica Federal do Paraná/UTFPR. E-mail: sandmann@utfpr.edu.br
4. Prof. Mestre, Universidade Tecnológica Federal do Paraná/UTFPR. E-mail: andrieled@utfpr.edu.br
5. Prof. Doutor, Universidade Tecnológica Federal do Paraná/UTFPR. E-mail: reinaldo@utfpr.edu.br
6. Prof. Mestre, Universidade Tecnológica Federal do Paraná/UTFPR. E-mail: celsohotz@utfpr.edu.br