HOME | ÍNDICE POR TÍTULO | NORMAS PUBLICACIÓN

Espacios. Vol. 36 (Nº 07) Año 2015. Pág. 12

Otimização de Rotas: Um estudo de caso em uma empresa do Setor Atacadista

Routes Optimization: a study case of a Wholesale Sector Company

Matheus Fernando MORO 1; Angela Regina BEM 2; Rena Alex Corrêa KANEZAWA 3; Guilherme BUENO 4

Recibido: 27/11/14 • Aprobado: 13/02/15

Contenido

1. Introdução

2. Materiais e métodos

3. Descrição do problema

4. Resultados e discussão

5. Considerações finais

6. Referências

1. Introdução

As transformações ocorridas nos últimos anos no ambiente dos negócios, tais como a abertura dos mercados e o aumento das exigências dos clientes, trouxeram às empresas dos mais diversos setores o aumento da concorrência, forçando-as a buscarem a otimização dos processos dentro de suas cadeias produtivas (RODRIGUES et al., 2014).

Com vistas à busca pelo aumento de sua competitividade frente a este novo mercado muitas empresas passaram a reavaliar suas funções organizacionais, destacando-se os investimentos realizados na função logística como um dos principais auxílios na busca desta competitividade. Nesse cenário, a logística adquire uma dimensão estratégica no gerenciamento de uma empresa, pois os serviços logísticos, quando bem estruturados, permitem a entrega de valores ao mercado (VASCONCELLOS et al., 2008).

Dentre as atividades logísticas destaque é dado às atividades de distribuição que, de acordo com Ballou (2008), representam cerca de 45% das despesas logísticas das empresas. Certamente, a sua otimização leva uma economia significativa dos recursos da empresa.

            Pureza e Lazarin (2010) afirmam que a busca pela eficiência na distribuição de bens ou serviços é um nicho a ser constantemente explorado. Tal eficiência pode ser obtida, dentre outros fatores, por meio de um adequado dimensionamento e planejamento de rotas para as frotas de veículos. Esta motivação levou ao surgimento e consolidação da classe de problemas de roteamento.

O objetivo deste trabalho é minimizar a rota de distribuição de uma empresa do setor atacadista de plástico, aplicando heurísticas de melhoramento do Problema do Caixeiro Viajante: Heurística do Subcircuito Inverso e Heurística do Vizinho mais Próximo, para assim, contribuir como uma alternativa na diminuição dos custos que a empresa tem com esse processo.

2. Materiais e métodos

O primeiro problema de roteirização a ser estudado foi o do folclórico caixeiro viajante (no inglês "traveling salesman problem" ou TSP), que consiste em encontrar o roteiro ou sequência de cidades a serem visitadas por um caixeiro viajante que minimize a distância total percorrida e assegure que cada cidade seja visitada exatamente uma vez (CUNHA, 1997).

O Problema do Caixeiro Viajante (PCV) tem sido muito utilizado no experimento de diversos métodos de otimização por ser, principalmente, um problema de fácil descrição e compreensão, porém com grande dificuldade de solução, uma vez que é NP-Árduo com larga aplicabilidade (PRESTES, 2013).

Sendo um grafo G = (N,E) onde N = {1,...,n} e o conjunto de nos e E = {1,...,m} e o conjunto de arestas de G, e custos, cij, associados com cada aresta ligando os vértices i e j, o problema consiste em localizar o menor ciclo Hamiltoniano do grafo G. O tamanho do ciclo e calculado pelo somatório dos custos das arestas que formam o ciclo. Os nos do grafo são, frequentemente, referenciados como "cidades" e, em outras palavras, o objetivo e visitar todas as cidades passando apenas uma vez por cada cidade, retornando ao ponto de origem. Este percurso deve ser feito de forma a minimizar a distancia total percorrida.

2.1. Formulação do PCV

Dado um conjunto C = {c1, ...,cn} de n cidades ci e uma matriz de distâncias (pij), onde pij = p(ci, cj) (i , j Є {1, ..., n} pij = pij ,pij = 0), a tarefa passa por encontrar a permutação π  Є Sn = {s : {1,..., n} → {1,..., n}} que faça com que a função objetivo (distância do circuito) f : Sn → |R, onde

atinja o seu mínimo.

O tamanho do espaço de procura aumenta exponencialmente dependendo de n, o número de cidades, uma vez que existem

circuitos possíveis (a posição inicial é arbitrária, e a ordem do circuito pode ser invertida).

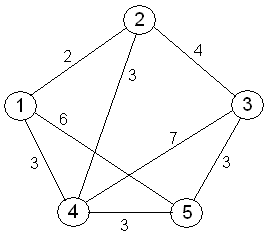
Figura 1 -  Problema do Caixeiro Viajante
Fonte -  GUEDES, (2013)

Dependendo da importância que poderá ter o sentido das setas (arestas), entre nós, o PCV pode-se distinguir em simétrico ou assimétrico (GUEDES, 2013).

O PCV é chamado simétrico quando a distância entre dois nós (ou cidades) quaisquer i e j independe do sentido, isto é, quando dij = dji; caso contrário o problema é denominado assimétrico. Segundo Helsgaun (2000), problemas simétricos são, em geral, mais difíceis de serem resolvidos que problemas assimétricos. Esse estudo é classificado como PCV simétrico, pois as distâncias entre as cidades independe do sentido da rodovia.

 2.2. Métodos para solução do PCV

A solução do PCV pode ser determinada por diferentes métodos. Estes, podem ser agrupados em métodos exatos e heurísticos. Os primeiros têm por base procedimentos branch-and-bound, isto é, de enumeração implícita em árvore onde é necessário inserir um limite inferior, no leque de soluções do problema. Existem limites inferiores triviais, como por exemplo, o elemento mínimo das soluções encontradas. Contudo, estes tipos de métodos demonstram muita dificuldade quando aplicados a problemas muito complexos, isto é, um PCV com muitas cidades, uma vez que a árvore de enumeração é muito extensa (CONWAY, 2003).

Os métodos heurísticos são procedimentos bastante particulares, o que os torna inflexíveis para a determinação de boas soluções para outro problema ligeiramente diferente (APLEGLATE, 2006).  Os métodos heurísticos são procedimentos que tem como objetivo encontrar soluções não necessariamente ótimas, mas que se aproximam do ponto ótimo do problema (BÄCK, 1996).

Neste trabalho, iremos utilizar dois métodos heurísticos que serão programados no software SCILAB® 5.3, as heurísticas são apresentadas a seguir.

As cidades que o atacado possui clientes, ou seja, cidades que o caminhão faz a distribuição foram disponibilizadas pela empresa. Os dados das distâncias entre as cidades foram retirados do Google maps.

2.2.1. Heurística do Subcircuito Inverso

Começa com um circuito viável e tenta melhorá-lo invertendo subcircuitos de duas cidades, 3 cidades, até subcircuitos com n-1 cidades (TEIXEIRA, 2012).

2.2.2. Heurística do Vizinho Mais Próximo

É caracterizado pela escolha da cidade mais próxima, sempre que o caixeiro se desloque, até que todas as cidades sejam visitadas.

Comece o algoritmo pela cidade i (i=1,2,...,n), em seguida ligue a cidade i com a cidade j (j=1,2,...,n), sendo j a cidade mais próxima de i. Repita o procedimento até que seja concluído o circuito com as n cidades (TEIXEIRA, 2012).

3. Descrição do problema

Empresas atacadistas são organizações intermediárias que se situam entre a indústria e o varejo. Têm como principal função ajustar as discrepâncias entre produção e consumo permitindo o aumento das economias nos custos de transação entre os elos produtor e consumidor (SILVA, 2010).

Enomoto (1997) afirma que a principal preocupação da empresa atacadista é a entrega no tempo correto em detrimento de custos e racionalizações. Enomoto (1997), ainda observa que as rotas de entrega são muitas vezes calculadas manualmente, o que pode levar a soluções muito distantes das soluções ótimas.

A empresa em estudo é do setor atacadista de plástico, faz a distribuição de plástico bolha para grande parte do estado do Paraná. Criada em 2001 em Guarapuava-PR, a empresa vem crescendo anualmente. O empresário, proprietário do estabelecimento afirmou que a empresa desde sua criação calcula sua rota manualmente e de acordo com o conhecimento do motorista.

A empresa considerada de pequeno porte, possui apenas um caminhão, de 5 eixos, para fazer a distribuição no estado. A distribuição é feita uma vez por semana, sempre para as mesmas 19 cidades. As cidades com clientes podem ser observadas do Quadro 1, ressalta-se que o ponto A, é a cidade sede da empresa, Guarapuava, onde o caminhão parte, percorrendo as outras 19 cidades e volta para seu destino inicial.

Quadro 1 - Pontos de distribuição
Fonte - Autores (2014)

A Figura 2 representa a localização no mapa das 20 cidades percorridas no Paraná. No indicador em verde, está representada a cidade que possui a sede da empresa, Guarapuava, já os outros indicadores em vermelho são representados as cidades clientes do atacado.

Figura 2 -  Localização das cidades clientes do atacado em estudo
Fonte - Autores (2014)

As distâncias entre os pontos de entrega (cidades de distribuição do atacado) são apresentadas no Quadro 2. Essas distâncias compõe a matriz distância, usada na resolução do problema.  As células com 0 (zero) significa que não existe um grafo direto entre os pontos de coleta, portanto essas distâncias são consideradas infinitas para resolução deste problema.

Quadro 2 – Matriz distância em km entre os pontos de entrega
Fonte  - Google Maps (2014)

A empresa juntamente com seu motorista estabeleceu uma rota a qual é empregada pelo caminhão que faz a distribuição de plástico bolha, a rota é definida nessa sequencia: A – Q – O – P – N – M – J – L – K – H – G – E – I – F – B – C – D – T – R – S – A, o percurso pode ser observado na Figura 3, totalizando um distância percorrida de 2103 km, o caminhão faz esse trajeto uma vez por semana.

Figura 3 -  Rota atual empregada pelo caminhão

Fonte - Autores (2014)

 4. Resultados e discussão

Optou-se pelo programa computacional SCILAB® 5.2.2 para encontrar o melhor roteiro para o problema. Elaborou-se um algoritmo para a resolução com os métodos heurísticos: vizinho mais próximo e subcircuito inverso.  Através da programação das heurísticas os resultados encontrados são apresentados na Figura 3 e 4, para as heurísticas do Vizinho mais próximo e Subcircuito inverso, consequentemente.

Figura 4 - Rota encontrada pela heurística do Vizinho mais próximo
Fonte - Autores (2014)

----

Figura 5 - Rota encontrada pela heurística do Subcircuito inverso
Fonte - Autores (2014)

-----

Os resultados obtidos pelas duas heurísticas podem ser comparados no Quadro 3 com a rota inicial.

Quadro 3 - Comparação entre as rotas obtidas e a atual
 Fonte - Autores (2014)

Pode-se perceber que para ambas as heurísticas o resultado obtido se mostrou melhor que a rota atualmente empregada pelo caminhão. Na heurística do Vizinho mais próximo, obteve-se uma melhora de 9,4 %, já o resultado encontrado pelo Subcircuito Inverso, diminui a rota em 10,5%.

Levando em conta que em muitas das rodovias percorridas pelo caminhão, há cobrança de pedágio, resolveu-se fazer um levantamento do preço do pedágio para cada uma dessas rotas, para contribuir na ajuda na tomada de decisão de qual seria a melhor rota, já que a diferença entre as duas rotas encontradas é de apenas 23 km. No Quadro 4, pode-se visualizar a comparação entre a rota, distância e preço total de pedágio.

Quadro 4 - Levantamento do preço do pedágio em cada rota
Fonte - Autores (2014)

A heurística do Subcircuito Inverso encontrou uma rota menor que a da heurística do Vizinho mais Próximo, porém a diferença entre o preço pago de pedágio entre as duas é de R$ 80,00 a mais para a rota do Subcircuito Inverso e distância de 23 km a mais para a rota do Vizinho mais Próximo.

Levando em consideração que o caminhão faz em média 4,5 quilômetros por litro de óleo diesel e que o preço do litro do óleo diesel está em aproximadamente R$ 2,48, o custo para o caminhão percorrer 23 km é de aproximadamente R$ 12,70, descontando da diferença do preço de pedágio, a rota encontrada pelo Vizinho mais Próximo ainda se sobressai em relação à rota do Subcircuito Inverso em R$ 67,30.

No Quadro 5, é apresentado a economia das duas rotas encontradas pelas heurísticas em relação a rota atualmente empregada.

Quadro 5 - Comparativa da economia das rotas em até um ano
Fonte -  Autores (2014)

Através do Quadro 5, percebemos que a economia em pedágio em um ano da rota do Vizinho mais Próximo é de R$ 5328,00, muito mais expressiva que a do Subcircuito Inverso, R$ 1488,00. Enquanto a diferença de distância entre as duas rotas depois de um ano é de 1104 km a menos para a rota da heurística do Subcircuito Inverso.

5. Considerações finais

Com o objetivo de minimizar a rota de distribuição de uma empresa do setor atacadista de plástico os métodos empregados se mostraram eficientes, já que se obteve um ganho aproximado de 9,4% para a heurística do Vizinho mais próximo e de 10,5% para a do Subcircuito Inverso, em relação à rota atual.

Acrescentado ao objetivo foi proposto uma comparação dos preços do pedágio em cada uma das rotas e verificou-se uma disparidade grande entre as duas rotas encontradas. A heurística do Subcircuito Inverso que obteve uma rota melhor que a outra heurística, apresentou um preço de pedágio muito mais elevado que a rota do Vizinho mais próximo, R$ 80,00 de diferença por viagem. Por fim, foi realizado um cálculo para verificar qual o custo da quilometragem de diferença das rotas encontradas (23km), e encontrou-se aproximadamente R$ 12,70, um valor menor que a diferença de pedágio.

Conclui-se então que a empresa do setor atacadista de plásticos, situada na cidade de Guarapuava-PR, deve mudar a rota de distribuição de seus produtos, escolhendo a rota do Vizinho mais Próximo (A – R – S – T – D – C – B – I – F – E – G – H – J – M –N – K – L – O – P – Q – A), pois mesmo sendo encontrada uma distância maior que a da outra rota, compensa pela diferença do preço do pedágio a ser pago. No fim de um ano a empresa além de economizar em combustível por 9504 km a menos, economizará também R$ 5328,00 em pedágios.

Este estudo apresentou um exemplo de como a utilização de ferramentas e tecnologias pode levar as organizações a elevados patamares de competitividade. A preocupação que algum tempo atrás era por estímulo de demanda, tem foco hoje na melhor gestão dos suprimentos, e a otimização de roteirização é um claro exemplo de redução de custos logísticos aperfeiçoando assim a cadeia de suprimentos.

6. Referências

APPLEGATE, David L. [et al.] – The travelling salesman problem: a computational Study. Princeton: Princeton University Press, 2006. ISBN 978-0-691-12993-8 

BäCK, Thomas – Evolutionary algorithms in theory and practice. New York: Oxford University Press, 1996. ISBN 978-0-195-09971-3

BALLOU, R.H. Logística Empresarial: transporte, administração de matérias e distribuição física. São Paulo: Atlas, 2008.

CONWAY, Richard Walter; MAXWELL, William L.; MILLER, Louis W. – Theory of scheduling. Reading, [Mass]: Edição de Courier Dover Publications, 2003. ISBN 978-0-486-42817-8 

CUNHA, C. B. Aspectos práticos da aplicação de modelos de roteirização de veículos a problemas reais. Revista Transporte, v. 8, n. 2, p. 51-74, nov., 2000.

ENOMOTO, L.M.; LIMA, R.S. Análise da distribuição física e roteirização em um atacadista. Revista Produção, v. 17, n. 1, p. 094-108, jan./abr. 2007.

GOOGLE MAPS.  Disponível em: http://maps.google.com.br/maps?hl=pt-BR&tab=ll. Acesso em: 15 de jun. 2014.

GUEDES, Allison da Costa Neves; LEITE, Jéssica Neiva de Figueiredo; ALOISE, Dário José – Um algoritmo genético com infecção viral para o problema do caixeiro viajante. Natal [Brasil]: Revista On Line de Iniciação Científica, 2005. Acesso em 21 de Junho de 2014. Disponível em: <:http://www.propesq.ufrn.br/publica/artigos-1edicao/et/MSIC-ET-011.pdf>

Helsgaun, K. (2000). An effective implementation of the Lin-Kernigham Traveling Salesman Heuristic, European Journal of Operational Research, v.126, p.106-130.

NEVES, M.F. Um modelo para planejamento de canais de distribuição no setor de alimentos. 1999. 297 f. Tese (Doutorado) – Faculdade de Economia, Administração e Contabilidade, USP, São Paulo, 1999.

PRESTES, A.N. Uma análise experimental de abordagens heurísticas aplicadas ao problema do caixeiro viajante. Universidade Federal do Rio Grande do Norte, Natal, jul. 2006. Disponível em: http://ftp.ufrn.br/pub/biblioteca/ext/bdtd/AlvaroNP.pdf. Acesso em: 22 jun. 2014.

PUREZA, V.; LAZARIN, D.F. Um estudo de impactos do roteamento dinâmico de veículos em atividades de prestação de serviço. Revista Produção, v. 20, n. 4, p. 589-600, out./dez., 2010.

RODRIGUES, M. R.; REBELATO, M. G.; GARCIA, C.C.  Estudo das atividades de distribuição e armazenagem em uma rede de supermercados do interior paulista. In: XXXIV Encontro Nacional de Engenharia de Produção. Curitiba: ABEPRO, 2014.

SILVA, A.M. Viabilidade econômica no canal de distribuição: estudo de caso em empresa atacadista. Periódico de Divulgação Científica da FALS, ano 3, n. 4, out./jan. 2010.

TEIXEIRA, L.L. Roteiro de Estudos. Universidade Tecnológica Federal do Paraná, Medianeira, 2011. Disponível em:  http://www.md.utfpr.edu.br/Intranet/professores/index.php?idusuario=158. Acesso em: 26 jun. 2014.

VASCONCELLOS, T. C.; MARINS, F. A. S.; MUNIZ JUNIOR, J. Implantação do método Activity Based Costing na logística interna de uma empresa química. Revista Gestão & Produção, vol. 15, n. 2, 2008.

1 UTFPR - Universidade Tecnológica Federal do Paraná - Brasil – Graduação em Engenharia de Produção. E-mail: morosmi@hotmail.com
2 UTFPR - Universidade Tecnológica Federal do Paraná - Brasil – Graduação em Engenharia de Produção. E-mail: angelaregina.bem@gmail.com
3 UTFPR - Universidade Tecnológica Federal do Paraná - Brasil – Graduação em Engenharia de Produção. E-mail: renan.ack@hotmail.com
4 UTFPR - Universidade Tecnológica Federal do Paraná - Brasil – Graduação em Engenharia de Produção. E-mail: gui.itu.sas@hotmail.com